1.6: The Volume of Cored Sphere

Last updated
Save as PDF

Page ID: 36009

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

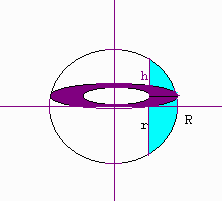
Let $S$ be a sphere of radius $R$, center at the origin and let $C$ be a cylinder of radius $r$ ($r < R$) with the z-axis the axis of rotation. We are concerned with the volume of the part of $S$ outside $C$. This cored sphere can also be realized by taking the region bounded by the circle

\[ x^2 + y^2 = R^2 \]

and the line

\[ x = r \]

and revolving it around the $y$-axis. Taking a cross-section perpendicular to the y-axis and revolving it around the y-axis produces a washer. The inner radius of the washer is $r$ and the square of the outer radius of the washer is

\[ R^2 - y^2\]

Let h be the the height of the region (from the x-axis).

\[ h = R^2 - r^2\]

Hence the area of the washer is

\[ Area = p[(R^2 - y^2 ) - r^2] = p[(R^2 - r^2 ) - y^2] = p[h^2 - y^2]\]

The smallest $y$ value the cross-section will have is $-h$ and the largest is $h$.

We can write this as an integral

\[\begin{align*} \pi \int_{-h}^{h}\left(h^{2}-y^{2}\right) dy &=\pi\left(h^{2} y-\frac{1}{3} y^{3}\right]_{-h}^{h} \\[4pt] &=\pi\left[\left(h^{3}-\frac{1}{3} h^{3}\right)-\left((-h)^{3}-\frac{1}{3}(-h)^{3}\right)\right] \\[4pt] &=\frac{4}{3} \pi h^{3} \end{align*}\]

$sphercyl.gif$

Notice that the volume only depends on the height of the region.