1.4: Countable and Uncountable Sets
- Page ID
- 60297
Definition 1.18
A set \(S\) is countable if there is a bijection \(f : \mathbb{N} \rightarrow S\). An infinite set for which there is no such bijection is called uncountable.
Proposition 1.19
Every infinite set \(S\) contains a countable subset.
Proposition 1.19
Every infinite set \(S\) contains a countable subset.
- Proof
-
Choose an element \(s_{1}\) from \(S\). Now \(S-\{s_{1}\}\) is not empty because \(S\) is not finite. So, choose \(s_{2}\) from \(S-\{s_{1}\}\). Then \(S-\{s_{1}, s_{2}\}\) is not empty because \(S\) is not finite. In this way, we can remove \(s_{n+1}\) from \(S-\{s_{1}, s_{2}, \cdots, s_{n}\}\) for all \(n\). Then set \(\{s_{1}, s_{2}, \cdots\}\) is countable and is contained in \(S\).
So countable sets are the smallest infinite sets in the sense that there are no infinite sets that contain no countable set. But there certainly are larger sets, as we will see next.
Theorem 1.20
The set \(\mathbb{R}\) is uncountable.
- Proof
-
The proof is one of mathematics’ most famous arguments: Cantor’s diagonal argument [8]. The argument is developed in two steps .
Let \(T\) be the set of semi-infinite sequences formed by the digits 0 and 2. An element \(t \in T\) has the form \(t = t_{1}t_{2}t_{3} \dots\) where \(t_{i} \in \{0, 2\}\). The first step of the proof is to prove that \(T\) is uncountable. So suppose it is countable. Then a bijection \(t\) between \(\mathbb{N}\) and \(T\) allows us to uniquely define the sequence \(t(n)\), the unique sequence associated to \(n\). Furthermore, they form an exhaustive list of the elements of \(T\). For example,
\[t(1) = \textbf{0},0,0,0,0,0,0,0,0,0,0, \dots \nonumber\]
\[t(2) = 2, \textbf{0},2,0,2,0,2,0,2,2,2, \dots \nonumber\]
\[t(3) = 0,0, \textbf{0},2,2,2,2,2,2,2,2, \dots \nonumber\]
\[t(4) = 2,2,2, \textbf{2},2,2,0,0,0,0,0, \dots \nonumber\]
\[t(5) = 0,0,0,2, \textbf{2},0,2,0,0,2,0, \dots \nonumber\]
\[t(6) = 2,0,0,0,0, \textbf{2},0,0,0,2,2, \dots \nonumber\]
\[\vdots \nonumber\]
Construct \(t^{*}\) as follows: for every \(n\), its nth digit differs from the nth digit of \(t(n)\). In the above example, \(t^{*} = \textbf{2}, \textbf{2}, \textbf{2}, \textbf{0}, \textbf{2}, \textbf{0}, \dots\). But now we have a contradiction, because the element \(t^{*}\) cannot occur in the list. In other words, there is no surjection from \(\mathbb{N}\) to \(T\). Hence there is no bijection between \(\mathbb{N}\) and \(T\).
The second step is to show that there is a subset \(K\) of \(\mathbb{R}\) such that there is no surjection (and thus no bijection) from \(\mathbb{N}\) to \(K\). Let \(t\) be a sequence with digits \(t_{i}\). Define \(f : T \rightarrow \mathbb{R}\) as follows
\[f(t) = \sum_{i=1}^{\infty}t_{i}3^{-i} \nonumber\]
If \(s\) and \(t\) are two distinct sequences in \(T\), then for some \(k\) they share the first \(k-1\) digits but \(t_{k} = 2\) and \(s_{k} = 0\). So
\[f(t)-f(s) = 2 \cdot 3^{-k}+\sum_{i=k+1}^{\infty} (t_{i}-s_{i}) 3^{-i} \ge 2 \cdot 3^{-k}-2 \sum_{i=k+1}^{\infty} 3^{-i} = 3^{-k} \nonumber\]
Thus \(f\) is injective. Therefore \(f\) is a bijection between \(T\) and the subset \(K = f(T)\) of \(\mathbb{R}\). If there is a surjection \(g\) from \(\mathbb{N}\) to \(K = f(T)\), then,
\[\mathbb{N} \xrightarrow{\text{g}} K \xleftarrow{\text{f}} T \nonumber\]
And so \(f^{-1} g\) is a surjection from \(\mathbb{N}\) to \(T\). By the first step, this is impossible. Therefore, there is no surjection \(g\) from \(\mathbb{N}\) to \(K\), much less from \(\mathbb{N}\) to \(\mathbb{R}\).
Corollary 1.21
(i) The set of infinite sequences in \(\{1,2,\cdots, b-1\}^{\mathbb{N}}\) is uncountable.
(ii) The set of finite sequences (but without bound) in \(\{1, 2, \cdots, b-1\}^{\mathbb{N}}\) is countable.
- Proof
-
The proof of (i) is the same as the proof that \(T\) is uncountable in the proof of Theorem 1.20. The proof of (ii) consists of writing first all \(b\) words of length 1, then all \(b^{2}\) words of length 2, and so forth. Every finite string will occur in the list.
Theorem 1.22
(i) The set \(\mathbb{Z}^2\) is countable.
(ii) \(\mathbb{Q}\) is countable.
- Proof
-
(i) The proof relies on Figure 2. In it, a directed path \(\gamma\) is traced out that passes through all points of \(\mathbb{Z}^2\). Imagine that you start at \((0, 0)\) and travel along \(\gamma\) with unit speed. Keep a counter \(c \in \mathbb{N}\) that marks the point \((0, 0)\) with a “1”. Up the value of the counter by 1 whenever you hit a point of \(\mathbb{Z}^2\). This establishes a bijection between \(\mathbb{N}\) and \(\mathbb{Z}^2\).
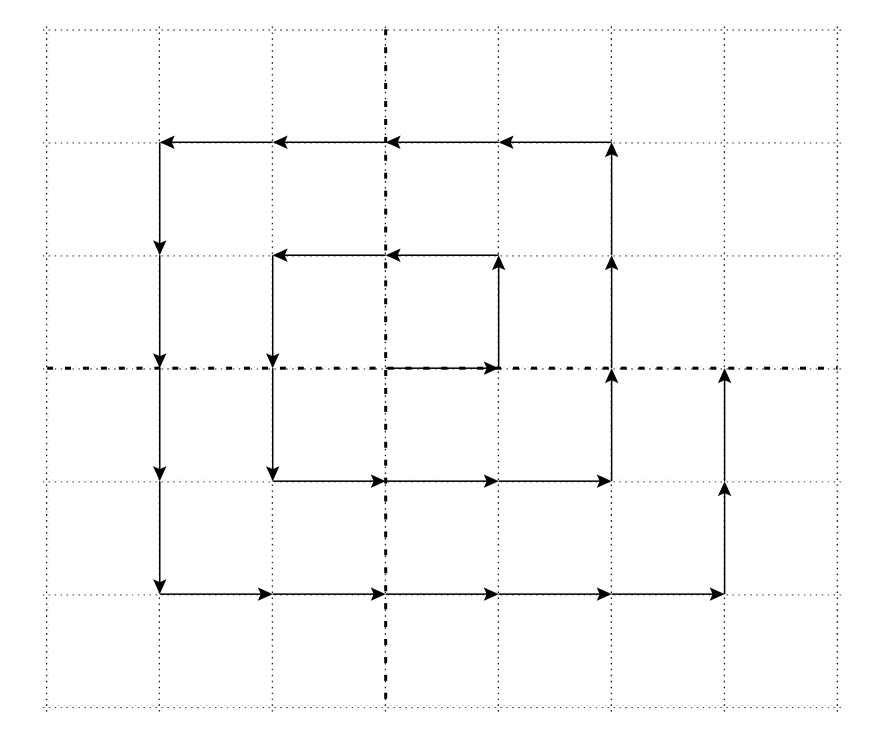
Figure 2. A directed path \(\gamma\) passing through all points of \(\mathbb{Z}^2\).
(ii) Again travel along \(\gamma\) with unit speed. Keep a counter \(c \in \mathbb{N}\) that marks the point \((0, 1)\) with a “1”. Up the value of the counter by 1. Continue to travel along the path until you hit the next point \((p, q)\) that is not a multiple of any previous and such \(q\) is not zero. Mark that point with the value of the counter. \(\mathbb{Q}\) contains \(\mathbb{N}\) and so is infinite. Identifying each marked point \((p, q)\) with the rational number \(\frac{p}{q}\) establishes the countability of \(\mathbb{Q}\).
Notice that this argument really tells us that the product of a countable set and another countable set is still countable. The same holds for any finite product of countable set. Since an uncountable set is strictly larger than a countable, intuitively this means that an uncountable set must be a lot largerthan a countable set. In fact, an extension of the above argument shows that the set of algebraic numbers numbers is countable. And thus, in a sense, it forms small subset of all reals. All the more remarkable, that almost all reals that we know anything about are algebraic numbers, a situation we referred to at the end of Section 1.4.
It is useful and important to have a more general definition of when two sets “have the same number of elements”.
Definition 1.23
Two sets A and B are said to have the same cardinality if there is a bijection \(f : A \rightarrow B\). It is written as \(|A| = |B|\). If there is an injection \(f : A \rightarrow B\), then \(|A| \le |B|\).
Definition 1.24
An equivalence relation on a set \(A\) is a (sub)set \(\mathbb{R}\) of ordered pairs in \(A \times A\) that satisfy three requirements.
- \((a, a) \in \mathbb{R}\) (reflexivity).
- If \((a, b) \in \mathbb{R}\), then \((b, a) \in \mathbb{R}\) (symmetry).
- If \((a, b) \in \mathbb{R}\) and \((b, c) \in \mathbb{R}\), then If \((a, c) \in \mathbb{R}\) (transitivity).
Usually \((a, b) \in \mathbb{R}\) is abbreviated to \(a \sim b\). The mathematical symbol “\(=\)” is an equivalence.
It is easy to show that having the same cardinality is an equivalence relation on sets (exercise 1.23). Note that the cardinality of a finite set is just the number of elements it contains. An excellent introduction to the cardinality of infinite sets in the context of naive set theory can be found in [15].


