3.4: The General Solution of ax+by = c

Last updated
Save as PDF

Page ID: 60311

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definition 3.8

Let $r_{1}$ and $r_{2}$ be given. The equation $r_{1}x + r_{2}y = 0$ is called homogeneous. The equation $r_{1}x + r_{2}y = c$ when $c \ne 0$ is called inhomogeneous. An arbitrary solution of the inhomogeneous equation is called a particular solution. By general solution, we mean the set of all possible solutions of the full (inhomogeneous) equation.

It is useful to have some geometric intuition relevant to the equation $r_{1}x + r_{2}y = c$. In $\mathbb{R}^2$, we set $\vec{r} = (r_{1}, r_{2}), \vec{x} = (x, y)$, etcetera. The standard inner product is written as $(\cdot, \cdot)$. The set of points in $\mathbb{R}^2$ satisfying the above inhomogeneous equation thus lie on the line $m \subset \mathbb{R}^2$ given by $(\vec{r}, \vec{x}) = c$.

This line is orthogonal to the vector $\vec{r}$ and its distance to the origin (measured along the vector $\vec{r}$) equals $\frac{|c|}{\sqrt{(\vec{r}, \vec{r})}}$. The situation is illustrated in Figure 7.

It is a standard result from linear algebra that the problem of finding all solutions of a inhomogeneous equation comes down to to finding one solution of the inhomogeneous equation, and finding the general solution of the homogeneous equation.

Lemma 3.9

Let $(x^{(0)}, y^{(0)})$ be a particular solution of $r_{1}x+r_{2}y = c$. The general solution of the inhomogeneous equation is given by $(x^{(0)}+z_{1}, y^{(0)}+z_{2})$ where $(z_{1}, z_{2})$ is the general solution of the homogeneous equation $r_{1}x+ r_{2}y = 0$.

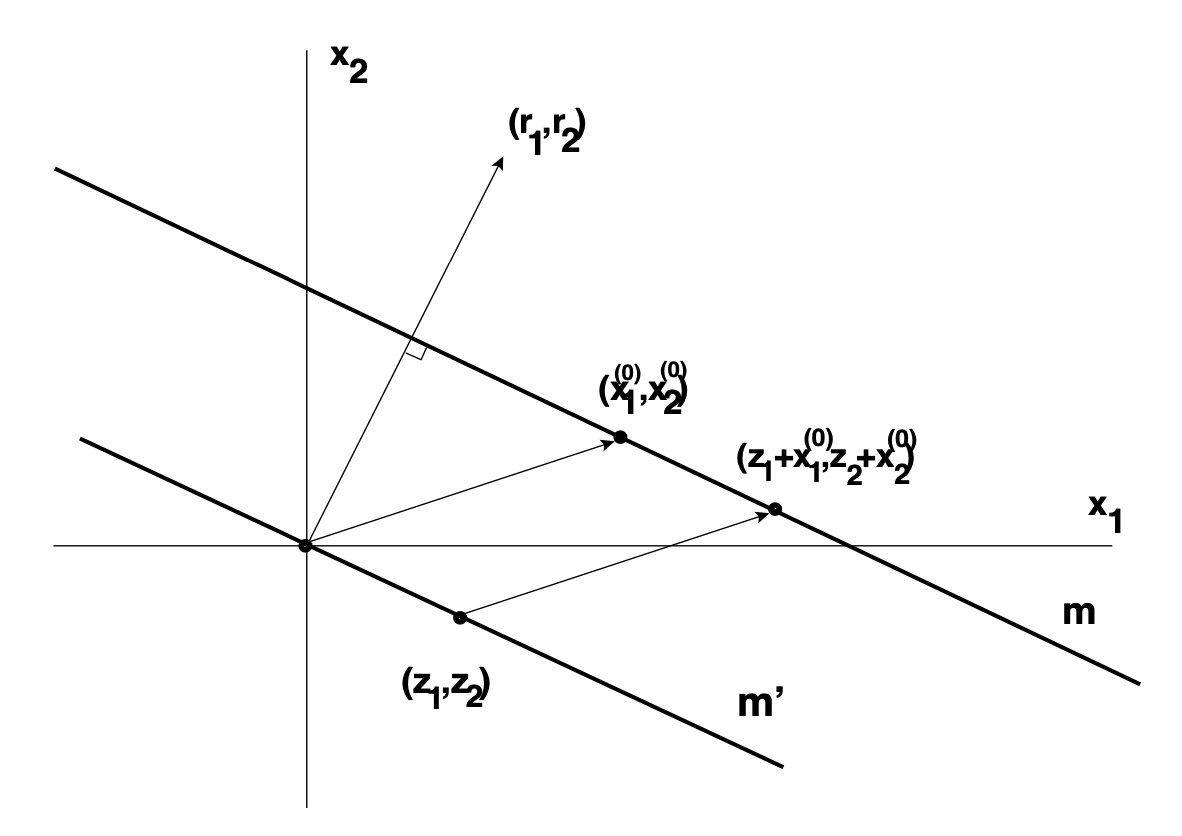
$Screen Shot 2021-04-23 at 3.40.29 PM.png$

Figure 7. The general solution of the inhomogeneous equation $(\vec{r}, \vec{x})= c$ in $\mathbb{R}^2$.

Proof: Let $(x^{(0)}, y^{(0)})$ be that particular solution. Let $m$ be the line given by $(\vec{r}, \vec{x})= c$. Translate $m$ over the vector $(-x^{(0)}, -y^{(0)})$ to get the line $m'$. Then an integer point on the line $m'$ is a solution $(z_{1}, z_{2})$ of the homogeneous equation if and only if $(x^{(0)}+z_{1}, y^{(0)}+z_{2})$ on $m$ is also an integer point (see Figure 7).

Be ́zout’s Lemma says that $r_{1}x + r_{2}y = c$ has a solution if and only if $\gcd (r_{1}, r_{2}) | c$. Theorem 3.4 gives a particular solution of that equation (via the Euclidean algorithm). Putting those results and Proposition 3.5 together, gives our final result.

Corollary 3.10

Given $r_{1}, r_{2}$, and $c$, the general solution of the equation $r_{1}x+r_{2}y = c$, where $\gcd(r_{1}, r_{2}) | c$, is the sum of the particular solution of Theorem 3.4 and the general solution of $r_{1} x+r_{2} y = 0$ of Proposition 3.5.