1.1: Compositions and Partitions
- Page ID
- 24658
We consider problems concerning the number of ways in which a number can be written as a sum. If the order of the terms in the sum is taken into account the sum is called a composition and the number of compositions of \(n\) is denoted by \(c(n)\). If the order is not taken into account the sum is a partition and the number of partitions of \(n\) is denoted by \(p(n)\). Thus, the compositions of 3 are
3 = 3, 3 = 1 + 2, 3 = 2 + 1, and 3 = 1 + 1 + 1,
so that \(c(3) = 4\). The partitions of 3 are
3 =3, 3 = 2 + 1, and 3 = 1 + 1 + 1,
so \(p(3) = 3\).
There are essentially three methods of obtaining results on compositions and partitions. First by purely combinatorial arguments, second by algebraic arguments with generating series, and finally by analytic operations on the generating series. We shall discuss only the first two of these methods.
We consider first compositions, these being easier to handle than partitions. The function \(c(n)\) is easily determined as follows. Consider \(n\) written as a sum of 1's. We have \(n - 1\) spaces between them and in each of the spaces we can insert a slash, yielding \(2^{n - 1}\) possibilities corrsponding to the \(2^{n - 1}\) composition of \(n\). For example
3 = 1 1 1, 3 = 1/1 1, 3 = 1 1/1, 3 = 1/1/1.
Just to illustrate the algebraic method in this rather trivial case we consider
\(\sum_{\infty}^{n = 1} c(n)x^n\).
It is easily verified that
\(\begin{array} {rcl} {\sum_{n = 1}^{\infty} c(n) x^n} &= & {\sum_{m = 1}^{\infty} (x + x^2 + x^3 + \cdot \cdot \cdot)^m} \\ {} &= & {\sum_{m = 1}^{\infty} (\dfrac{x}{1 - x})^m = \dfrac{x}{1 - 2x} = \sum_{n =1}^{\infty} x^{n - 1}x^n.} \end{array}\)
Example \(\PageIndex{1}\)
As an exercise I would suggest using both the combinatorial method and the algebraic approach to prove the following results:
- The number of compositions of \(n\) into exactly \(m\) parts is \({n - 1 \choose m -1}\) (Catalan);
- The number of compositions of \(n\) into even parts is \(2^{\dfrac{n}{2} - 1}\) if \(n\) is even and 0 if \(n\) is odd;
- The number of compositions of \(n\) into an even number of parts is equal to the number of compositions of \(n\) into an odd number of parts.
Solution
Add text here.
Somewhat more interesting is the determination of the number of compositions \(c^{*}(n)\) of \(n\) into odd parts. Here the algebraic approach yields
\(\begin{array} {rcl} {\sum_{n = 1} c^{*}(n) x^n} &= & {\sum_{m = 1}^{\infty} (x + x^3 + x^5 + \cdot \cdot \cdot)^m} \\ {} &= & {\sum_{m = 1}^{\infty} (\dfrac{x}{1 - x^2})^m = \dfrac{x}{1 - x - x^2} = \sum F(n) x^n.} \end{array}\)
By cross multiplying the last two expressions we see that
\(F_{n + 2} = F_{n} + F_{n + 1}\), \(F_0 = 0, F_1 = 1\)
Thus the F's are the so-called Fibonacci numbers
1, 1, 2, 3, 5, 8, 13, ....
The generating function yields two explicit expressions for these numbers. First, by “partial fractioning” \(\dfrac{x}{1 - x - x^2}\), expanding each term as a power series and comparing coefficients, we obtain
\(F_n = \dfrac{1}{\sqrt{5}}{(\dfrac{1 + \sqrt{5}}{2})^n - (\dfrac{1 - \sqrt{5}}{2})^n}.\)
Another expression for \(F_n\) is obtained by observing that
\(\dfrac{x}{1 - x - x^2} = x(1 + (x + x^2)^1 + (x + x^2)^2 + (x + x^2)^3 + \cdot\cdot\cdot).\)
Comparing the coefficients here we obtain (Lucas)
\(F_n = {n - 1 \choose 0} + {n - 2 \choose 1} + {n - 3 \choose 2} + \cdot\cdot\cdot).\)
You might consider the problem of deducing this formula by combinatorial arguments.
Suppose we denote by \(a(n)\) the number of compositions of n with all summands at most 2, and by b(n) the number of compositions of \(n\) with all summands at least 2. An interesting result is that \(a(n) = b(n + 2)\). I shall prove this result and suggest the problem of finding a reasonable generalization.
First note that \(a(n) = a(n − 1) + a(n − 2)\). This follows from the fact that every admissible composition ends in 1 or 2. By deleting this last summand, we obtain an admissible composition of \(n − 1\) and \(n − 2\) respectively. Since \(a(1) = 1\) and \(a(2) = 2\), it follows that \(a(n) = F_n\). The function \(b(n)\) satisfies the same recursion formula. In fact, if the last summand in an admissible composition of \(n\) is 2, delete it to obtain an admissible composition of \(n − 2\); if the last summand is greater than 2, reduce it by 1 to obtain an admissible composition of \(n − 1\). Since \(b(2) = b(3) = 1\), it follows that \(b(n) = F_{n−2}\) so that \(a(n)=F_n =b(n+2)\).
An interesting idea for compositions is that of weight of a composition. Suppose we associate with each composition a number called the weight, which is the product of the summands. We shall determine the sum \(w(n)\) of the weights of the compositions of \(n\). The generating function of \(w(n)\) is
\(\sum_{n = 1}^{\infty} w(n) x^n = \sum_{m = 1}^{\infty} (x + 2x^2 + 3x^3 + \cdot\cdot\cdot)^m = \dfrac{x}{1 - 3x + x^2}.\)
From this we find that \(w(n)=3w(n − 1) − w(n − 2)\). I leave it as an exercise to prove from this that \(w(n) = F_{2n−1}\).
We now turn to partitions. There is no simple explicit formula for \(p(n)\). Our main objective here will be to prove the recursion formula
\(p(n) = p(n - 1) + p(n - 2) - p(n - 5) - p(n - 7) + p(n - 12) + p(n - 15) + \cdot\cdot\cdot\)
discovered by Euler. The algebraic approach to partition theory depends on algebraic manipulations with the generating function
\(\sum_{n = 0}^{\infty} p(n)x^n = \dfrac{1}{(1 - x)(1 - x^2)(1 - x^3) \cdot\cdot\cdot}\)
and related functions for restricted partitions. The combinatorial approach depends on the use of partition (Ferrer) diagrams. For example the Ferrer diagram of the partition 7 = 4 + 2 + 1 is

Useful here is the notion of conjugate partition. This is obtained by reflecting the diagram in a \(45^{\circ}\) line going down from the top left corner. For example,
the partitions
 and
and 
are conjugate to each other. This correspondence yields almost immediately the following theorems:
The number of partitions of \(n\) into \(m\) parts is equal to the number of partitions of \(n\) into parts the largest of which is \(m\);
The number of partitions of \(n\) into not more than \(m\) parts is equal to the number of partitions of \(n\) into parts not exceeding \(m\).
Of a somewhat different nature is the following: The number of partitions of \(n\) into odd parts is equal to the number of partitions of \(n\) into distinct parts. For this we give an algebraic proof. Using rather obvious generating functions for the required partitions the result comes down to showing that
\(\dfrac{1}{(1 - x)(1 - x^3)(1 - x^5)(1 - x^7)\cdot\cdot\cdot} = (1 + x)(1 + x^2)(1 + x^3)(1 + x^4)\cdot\cdot\cdot.\)
Cross multiplying makes the result intuitive.
We now proceed to a more important theorem due to Euler:
\((1 - x)(1 - x^2)(1 - x^3)\cdot\cdot\cdot = 1 - x^1 - x^2 + x^5 + x^7 - x^{12} - x^{15} + \cdot\cdot\cdot,\)
where the exponents are the numbers of the form \(\dfrac{1}{2} k(3k \pm 1)\). We first note that
\((1 - x)(1 - x^2)(1 - x^3) \cdot\cdot\cdot = \sum((E(n) - O(n))x^n,\)
where \(E(n)\) is the number of partitions of \(n\) into an even number of distinct parts and \(O(n)\) the number of partitions of \(n\) into an odd number of distinct parts.
We try to establish a one-to-one correspondence between partitions of the two sorts considered. Such a correspondence naturally cannot be exact, since an exact correspondence would prove that \(E(n) = O(n)\).
We take a graph representing a partition of \(n\) into any number of unequal parts. We call the lowest line \(AB\) the base of the graph. From \(C\), the extreme north-east node, we draw the longest south-westerly line possible in the graph; this may contain only one node. This line \(CDE\) is called the wing of the graph
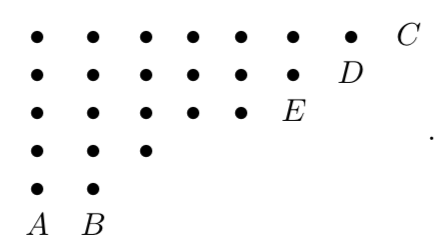
Usually we may move the base into position of a new wing (parallel and to the right of the “old” wing). Sometimes we may carry out the reverse operation (moving the wing to be over the base, below the old base). When the operation described or its converse is possible, it leads from a partition with into an odd number of parts into an even number of parts or conversely. Thus, in general \(E(n) = O(n)\). However two cases require special attention,. They are typified by the diagrams
 and
and 
In these cases \(n\) has the form
\(k + (k + 1) + \cdot\cdot\cdot + (2k - 1) = \dfrac{1}{2} (3k^2 - k)\)
and
\((k + 1) + (k + 2) + \cdot\cdot\cdot + (2k) = (3k^2 + k)\).
In both these cases there is an excess of one partition into an even number of parts, or one into an odd number, according as \(k\) is even or odd. Hence \(E(n) - O(n) = 0\), unless \(n = \dfrac{1}{2}(3k \pm k)\), when \(E(n) - O(n) = (-1)^k\). This gives Euler's theorem.
Now, from
\(\sum p(n) x^n (1 - x - x^2 + x^5 + x^7 - x^{12} - \cdot\cdot\cdot) = 1\)
we obtain a recurrence relation for \(p(n)\), namely
\(p(n) = p(n - 1) + p(n - 2) - p(n - 5) - p(n - 7) + p(n - 12) + \cdot\cdot\cdot.\)


