1.3: Distribution of Primes
- Page ID
- 24672
Perhaps the best known proof in all of “real” mathematics is Euclid’s proof of the existence of infinitely many primes.
Theorem \(\PageIndex{1}\): existence of infinitely many primes
If \(p\) were the largest prime then \((2 \cdot 3 \cdot 5 \cdot\cdot\cdot p) + 1\) would not be divisible by any of the primes up to \(p\) and hence would be the product of primes exceeding \(p\)
In spite of its extreme simplicity this proof already raises many exceedingly difficult questions, e.g., are the numbers \((2 \cdot 3 \cdot ... \cdot p) + 1\) usually prime or composite? No general results are known. In fact, we do not know whether an infinity of these numbers are prime, or whether an infinity are composite.
The proof can be varied in many ways. Thus, we might consider \((2 \cdot 3 \cdot 5 \cdot\cdot\cdot p) - 1\) or \(p! + 1\) or \(p! - 1\). Again almost nothing is known about how such numbers factor. The last two sets of numbers bring to mind a problem that reveals how, in number theory, the trivial may be very close to the most abstruse. It is rather trivial that for \(n > 2, n! - 1\) is not a perfect square. What can be said about \(n! + 1\)? Well, \(4! + 1 = 5^2\), \(5! + 1 = 11^2\) and \(7! + 1 = 71^2\). However, no other cases are known; nor is it known whether any other numbers \(n! + 1\) are perfect squares. We will return to this problem in the lectures on diophantine equations.
After Euclid, the next substantial progress in the theory of distribution of primes was made by Euler. He proved that \(\sum \dfrac{1}{p}\) diverges, and described this result by saying that the primes are more numerous than the squares. I would like to present now a new proof of this fact -- a proof that is somewhat related to Euclid's proof of the existence of infinitely many primes.
We need first a (well known) lemma concerning subseries of the harmonic series. Let \(p_1 < p_2 < ...\) be a sequence of positive integers and let its counting function be
\[\pi (x) = \sum_{p \le x} 1.\]
Let
\[R(x) = \sum_{p \le x} \dfrac{1}{p}.\]
Lemma
If \(R(\infty)\) exists then
\[\lim_{x \to \infty} \dfrac{\pi(x)}{x} = 0.\]
- Proof
-
\[\pi(x) = 1 (R(1) - R(0)) + 2 ((R(2) - R(1)) + ... + x(R(x) - R(x - 1))\]
or
\[\dfrac{\pi (x)}{x} = R(x) - \left[\dfrac{R(0) + R(1) + \cdot\cdot\cdot R(x - 1)}{x}\right].\]
Since \(R(x)\) approaches a limit, the expression within the square brackets approaches this limit and the lemma is proved.
In what follows we assume that the \(p\)'s are the primes.
To prove that \(\sum \dfrac{1}{p}\) diverges we will assume the opposite, i.e., \(\sum \dfrac{1}{p}\) converges (and hence also that \(\dfrac{\pi(x)}{x} \to 0\)) and derive a contradiction.
\[\sum_{p > n} \dfrac{1}{p} < \dfrac{1}{2}.\]
But now this \(n\) is fixed so there will also be an \(m\) such that
\[\dfrac{\pi (n!m)}{n!m} < \dfrac{1}{2n!}.\]
With such an \(n\) and \(m\) we form the \(m\) numbers
\(T_1 = n! - 1, T_2 = 2n! - 1, ..., T_m = mn! - 1.\)
Note that none of the \(T\)'s have prime factors \(\le n\) or \(\ge mn!\). Furthermore if \(p | T_i\) and \(p | T_j\) then \(p | (T_i - T_j)\) so that \(p | (i - j)\). In other words, the multiples of \(p\) are \(p\) apart in our set of numbers. Hence not more than \(\dfrac{m}{p} + 1\) of the numbers are divisible by \(p\). Since every number has at least one prime factor we have
\(\sum_{n < p < n! m} (\dfrac{m}{p} + 1) \ge m\)
or
\(\sum_{n< p} \dfrac{1}{p} + \dfrac{\pi (n!m)}{m} \ge 1.\)
But now by (1) and (2) the right hand side should be < 1 and we have a contradiction, which proves our theorem.
Euler’s proof, which is more significant, depends on his very important identity
\(\zeta (s) = \sum_{n = 1}^{\infty} \dfrac{1}{n^s} = \prod_{p} \dfrac{1}{1 - \dfrac{1}{p^s}}.\)
This identity is essentially an analytic statement of the unique factorization theorem. Formally, its validity can easily be seen. We have
\(\begin{array} {rcl} {\prod_{p} \dfrac{1}{1 - \dfrac{1}{p^s}}} & = & {\prod_p (1 + \dfrac{1}{p^s} + \dfrac{1}{p^{2s}} + \cdot\cdot\cdot)} \\ {} & = & {(1 + \dfrac{1}{2^s} + \cdot\cdot\cdot)(1 + \dfrac{1}{3^s} + \cdot\cdot\cdot)(1 + \dfrac{1}{5^s} + \cdot\cdot\cdot)} \\ {} & = & {\dfrac{1}{1^s} + \dfrac{1}{2^s} + \dfrac{1}{3^s} + \cdot\cdot\cdot.} \end{array}\)
Euler now argued that for \(s = 1\),
\(\sum_{n = 1}^{\infty} \dfrac{1}{n^s} = \infty\)
so that
\(\prod_p \dfrac{1}{1 - \dfrac{1}{p}}\)
must be infinite, which in turn implies that \(\sum \dfrac{1}{p}\) must be infinte.
This argument, although not quite valid, can certainly be made valid. In fact, it can be shown without much difficulty that
\(\sum_{n \le x} \dfrac{1}{n} - \prod_{p \le x} (1 - \dfrac{1}{p})^{-1}\)
is bounded. Since \(\sum_{n \le x} \dfrac{1}{n} - \text{log} x\) is bounded, we can, on taking logs, obtain
\(\text{loglog} x = \sum_{p \le x} - \text{log} (1 - \dfrac{1}{p}) + O(1)\)
so that
\(\sum_{p \le x} \dfrac{1}{p} = \text{loglog} x + O(1).\)
We shall use this result later.
Gauss and Legendre were the first to make reasonable estimates for \(\pi (x)\). Essentially, they conjectured that
\(\pi(x) \thicksim \dfrac{x}{\text{log} x},\)
the famous Prime Number Theorem. Although this was proved in 1896 by J. Hadamard and de la Vallee Poussin, the first substantial progress towards this result is due to Chebycheff. He obtained the following three main results:
- There is a prime between \(n\) and \(2n\) (\(n > 1\));
- There exist positive constants \(c_1\) and \(c_2\) such that \[\dfrac{c_2 x}{\text{log} x} < \pi (x) < \dfrac{c_1 x}{\text{log} x};\]
- If \(\dfrac{\pi (x)}{\text{log} x}\) approaches a limit, then that limit is 1.
We shall prove the three main results of Chebycheff using his methods as modified by Landau, Erd\(\ddot{\text{o}}\)s and, to a minor extent, L. Moser.
We require a number of lemmas. The first of these relate to the magnitude of
\(n!\) and \({2n \choose n}\).
As far as \(n!\) is concerned, we might use Stirling's approximation
\(n! \thicksim n^n e^{-n} \sqrt{2 \pi n}.\)
However, for our purposes, a simpler estimate will suffice. Since
\(\dfrac{n^n}{n!}\)
and we have the following lemma.
Lemma 1
\(n^n e^{-n} < n! < n^n\).
- Proof
-
Since
\((1 + 1)^{2n} = 1 + {2n \choose 1} + \cdot\cdot\cdot + {2n \choose n} + \cdot\cdot\cdot + 1,\)
it follows that
\({2n \choose n} < 2^{2n} = 4^n.\)
This estimate for \({2n \choose n}\) is not as crude as it looks, for it can be easily seen from Stirling's formula that
\({2n \choose n} \thicksim \dfrac{4^n}{\sqrt{\pi n}}.\)
Using induction we can show for \(n > 1\) that
\({2n \choose n} > \dfrac{4^n}{2n},\)
and thus we have
lemma 2
\(\dfrac{4^n}{2n} < {2n \choose n} < 4^n.\)
- Proof
-
Note that \({2n + 1 \choose n}\) is one of two equal terms in the expansion of \((1 + 1)^{2n + 1}\). Hence we also have
LEmma 3
\({2n + 1 \choose n} < 4^n.\)
- Proof
-
As an exercise you might use these to prove that if
\(n = a + b + c + \cdot\cdot\cdot\)
then
\(\dfrac{n!}{a! b! c! \cdot\cdot\cdot} < \dfrac{n^n}{a^ab^bc^c \cdot\cdot\cdot}.\)
Now we deduce information on how \(n!\) and \({2n \choose n}\) factor as the product of primes. Suppose \(e_p (n) is the exponent of the prime \(p\) in the prime power factorization of \(n!\), i.e.
\(n! = \prod p^{e_p (n)}.\)
We easily prove
lemma 4
(Legendre). \(e_p (n) = [\dfrac{n}{p}] + [\dfrac{n}{p^2}] + [\dfrac{n}{p^3}] + \cdot \cdot\cdot.\)
- Proof
-
In fact \([\dfrac{n}{p}]\) is the number of multiples of \(p\) in \(n!\), the term \([\dfrac{n}{p^2}]\) adds the additional contribution of the multiples of \(p^2\), and so on, e.g.,
\(e_3(30) = [\dfrac{30}{3}] + [\dfrac{30}{9}] + [\dfrac{30}{27}] + \cdot\cdot\cdot = 10 + 3 + 1 = 14.\)
An interesting and sometimes useful alternative expression for \(e_p (n)\) is given by
\(e_p(n) = \dfrac{n - s_p (n)}{p - 1}, \)
where \(s_p (n)\) represents the sum of the digits of \(n\) when \(n\) is expressed in base \(p\). Thus in base 3, 30 can be written 1010 so that \(e_3(30) = \dfrac{30 - 2}{2} = 14\) as before. We leave the proof of the general case as an exercise.
We next consider the composition of \({2n \choose n}\) as a product of primes. Let \(E_p(n)\) denote the exponent of \(p\) in \({2n \choose n}\), i.e.,
\({2n \choose n} = \prod_p p^{E_p(n)}.\)
Clearly
\(E_p (n) = e_p (2n) - 2 e_p (n) = \sum_i {[\dfrac{2n}{p^i}] - 2\ [\dfrac{n}{p^i}]}.\)
Our alternative expression for \(e_p(n)\) yields
\(E_p(n) = \dfrac{2s_p(n) - s_p(2n)}{p - 1}.\)
In the first expression each term in the sum can easily be seen to be 0 or 1 and the number of terms does not exceed the exponent of the highest power of \(p\) that does not exceed \(2n\). Hence
lemma 5
\(E_p(n) \le \text{log}_p (2n).\)
lemma 6
The contribution of \(p\) to \({2n \choose n}\) does not exceed \(2n\)
The following three lemmas are immediate.
lemma 7
Every prime in the range \(n < p < 2n\) appears exactly once in \({2n \choose n}\)
lemma 8
No prime in the range \(p > \sqrt{2n}\) appears more than once in \({2n \choose n}\)
Although it is not needed in what follows, it is amusing to note that since \(E_2(n) = 2s_2 (n) - s_2 (2n)\) and \(s_2(n) = s_2 (2n)\), we have \(E_2(n) = s_2(n)\).
As a first application of the lemmas we prove the elegant result
Theorem 1
\(\prod_{p \le n} p < 4^n\).
- Proof
-
The proof is by induction on \(n\). We assume the theorem true for integers \(< n\) and consider the cases \(n = 2m\) and \(n = 2m + 1\). If \(n = 2m\) then
\(\prod_{p \le 2m} p = \prod_{p \le 2m - 1} p < 4^{2m - 1}\)
by the induction hypothesis. If \(n = 2m + 1\) then
\(\begin{array} {rcl} {\prod_{p \le 2m + 1} p} & = & {(\prod_{p \le m + 1} p)(\prod_{m + 1 < p < 2m + 1} p)} \\ {} & < & {4^{m + 1} {2m + 1 \choose m} \le 4^{m + 1} 4^m = 4^{2m + 1}} \end{array}\)
and the induction is complete.
It can be shown by much deeper methods (Rosser) that
\(\prod_{p \le n} p < (2.83)^n.\)
Actually the prime number theorem is equivalent to
\(\sum_{p \le n} \text{log } p \thicksim n.\)
From Theorem 1 we can deduce
Theorem 2
\(\pi (n) < \dfrac{cn}{\text{log} n}. \)
- Proof
-
Clearly
\(4^n > \prod_{p \le n} p > \prod_{\sqrt{n} \le p \le n} p > \sqrt{n} ^{\pi (n) - \pi (\sqrt{n})}\)
Taking logarithms we obtain
\(n \text{log } 4 > (\pi(n) - \pi(\sqrt{n})) \dfrac{1}{2} \text{log } n)
or
\(\pi(n) - \pi(\sqrt{n}) < \dfrac{n \cdot 4 \text{log } 2}{\text{log } n}\)
or
\(\pi (n) < (4 \text{log } 2) \dfrac{n}{\text{log } n} + \sqrt{n} < \dfrac{cn}{\text{log } n}\).
Next we prove
Theorem 3
\(\pi(n) > \dfrac{cn}{\text{log} n}\).
- Proof
-
For this we use Lemmas 6 and 2. From these we obtain
\((2n)^{\pi(2n)} > {2n \choose n} > \dfrac{4^n}{2n}.\)
Taking logarithms, we find that
\((\pi (n) + 1) \text{log } 2n > \text{log } (2^{2n}) = 2n \text{log } 2.\)
Thus, for even \(m\)
\(\pi(m) + 1 > \dfrac{m}{\text{log } m} \text{log } 2\)
and the result follows.
We next obtain an extimate for \(S(x) = \sum_{p \le x} \dfrac{\text{log }p}{p}.\) Taking the logarithm of \(n! = \prod_p p^{e_p}\) we find that
\(n \text{log } n > \text{log } n! = \sum e_p (n) \text{log } p > n (\text{log } n - 1).\)
The reader may justify that the error introduced in replacing \(e_p(n)\) by \(\dfrac{n}{p}\) (of course \(e_p(n) = \sum [\dfrac{n}{p^i}]\)) is small enough that
\(\sum_{p \le n} \dfrac{n}{p} \text{log } p = n \text{log } n + O(n)\)
or
\(\sum_{p \le n} \dfrac{\text{log }p}{p} = \text{log } n + O(1)\).
We can now prove
Theorem 4
\(R(x) = \sum_{p \le x} \dfrac{1}{p} = \text{log log } x + O(1)\).
- Proof
-
In fact
\(\begin{array} {rcl} {R(x)} & = & {\sum_{n = 2}^{x} \dfrac{S(n) - S(n - 1)}{\text{log } n}} \\ {} & = & {\sum_{n = 2}^{x}S(n) (\dfrac{1}{\text{log } n} - \dfrac{1}{\text{log }(n + 1)}) + O(1)} \\ {} & = & {\sum_{n = 2}^{x} (\text{log } n + O(1)) \dfrac{\text{log }(1 + \dfrac{1}{n}}{(\text{log } n) \text{log } (n + 1)} + O(1)} \\ {} & = & {\sum_{n = 2}^{x} \dfrac{1}{n \text{log } n} + O(1)} \\ {} & = & {\text{log log } x + O(1)} \end{array}\)
as desired.
We now outline the proof of Chebycheff's
Theorem 5
If \(\pi(x) \thicksim \dfrac{cx}{\text{log }x}\), then \(c = 1\).
- Proof
-
Since
\(\begin{array} {rcl} {R(x)} &= & {\sum_{n = 1}^{x} \dfrac{\pi(n) - \pi(n - 1)}{n}} \\ {} &= & {\sum_{n = 1}^{x} \dfrac{\pi(n)}{n^2} + O(1)} \end{array}\)
\(\pi(x) \thicksim \dfrac{cx}{\text{log }x}\) would imply
\(\sum_{n = 1}^{x} \dfrac{\pi(n)}{n^2} \thicksim c\text{log log }x\).
But we already know that \(\pi(x) \thicksim \text{log log } x\) so it follows that \(c = 1\).
We next give a proof of Bertrand’s Postulate developed about ten years ago (L. Moser). To make the proof go more smoothly we only prove the somewhat weaker
Theorem 6: Bertrand’s Postulate
For every integer \(r\) there exists a prime \(p\) with
\(3 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r}\).
We restate several of our lemmas in the form in which they will be used.
- If \(n < p < 2n\) then \(p\) occurs exactly once in \({2n \choose n}\).
- If \(2 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r - 1}\) then \(p\) does not occur in \({3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}\).
- If \(p > 2^{r + 1}\) then \(p\) occurs at most once in \({3 \cdot 2^{2n} \choose 3 \cdot 2^{2n - 1}}\).
- No prime occurs more than \(2r + 1\) times in \({3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}\)
We now compare \({3 \cdot 2^{2r} \choose 3 \cdot 2^{2r - 1}}\) and
\({2^{2r} \choose 2^{2r - 1}} {2^{2r - 1} \choose 2^{2r - 2}} \cdot \cdot \cdot {2 \choose 1} {{2^{r + 1} \choose 2^r}{2^r \choose 2^{r - 1}} \cdot\cdot\cdot {2 \choose 1} }^{2r}.\)
Assume that there is no prime in the range \(3 \cdot 2^{2r - 1} < p < 3 \cdot 2^{2r}\). Then, by our lemmas, we find that every prime that occurs in the first expression also occurs in the second with at least as high a multiplicity; that is, the second expression in not smaller than the first. On the other hand, observing that for \(r \ge 6\)
\(3 \cdot 2^{2r} > (2^{2r} + 2^{2r - 1} + \cdot\cdot\cdot + 2) + 2r(2^{r + 1} + 2r + \cdot\cdot\cdot + 2),\)
and interpreting \({2n \choose n}\) as the number of ways of choosing \(n\) objects from \(2n\), we conclude that the second expression is indeed smaller than the first. This contradiction proves the theorem when \(r > 6.\) The primes 7, 29, 97, 389, and 1543 show that the theorem is also true for \(r \le 6\).
The proof of Bertrand’s Postulate by this method is left as an exercise.
Bertrand’s Postulate may be used to prove the following results.
(1) \(\dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}\) is never an integer.
(2) Every integer > 6 can be written as the sum of distinct primes.
(3) Every prime \(p_n\) can be expressed in the form
\(p_n = \pm 2 \pm 3 \pm 5 \pm \cdot\cdot\cdot \pm p_{n - 1}\)
with an error of at most 1 (Scherk).
(4) The equation \(\pi(n) = \varphi (n)\) has exactly 8 solutions.
About 1949 a sensation was created by the discovery by Erd ̋os and Selberg of an elementary proof of the Prime Number Theorem. The main new result was the following estimate, proved in an elementary manner:
\(\sum_{p \le x} \text{log}^2 p + \sum_{pq \le x} \text{log }p\text{log }q = 2x \text{log } x + O(x)\).
Although Selberg’s inequality is still far from the Prime Number Theorem, the latter can be deduced from it in various ways without recourse to any further number theoretical results. Several proofs of this lemma have been given, perhaps the simplest being due to Tatuzawa and Iseki. Selberg’s original proof depends on consideration of the functions
\(\lambda_n = \lambda_{n, x} = \sum_{d|n} \mu (d) \text{log}^2 \dfrac{x}{d}\)
and
\(T(x) = \sum_{n = 1}^{x} \lambda_n x^n\).
Some five years ago J. Lambek and L. Moser showed that one could prove Selberg’s lemma in a completely elementary way, i.e., using properties of inte- gers only. One of the main tools for doing this is the following rational analogue of the logarithm function. Let
\(h(n) = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}\) and \(\ell_k(n) = h(kn) - h(k).\)
We prove in an quite elementary way that
\(|\ell_k (ab) - \ell_k (a) - \ell_k (b)| < \dfrac{1}{k}.\)
The results we have established are useful in the investigation of the magnitude of the arithmetic functions \(\sigma_k(n)\), \(\varphi_k(n)\) and \(\omega_k(n)\). Since these depend not only on the magnitude of \(n\) but also strongly on the arithmetic structure of \(n\) we cannot expect to approximate them by the elementary functions of analysis. Nevertheless we shall will see that “on the average” these functions have a rather simple behavior.
If \(f\) and \(g\) are functions for which
\(f(1) + f(2) + \cdot\cdot\cdot + f(n) \thicksim g(1) + g(2) + \cdot\cdot\cdot g(n)\)
we say that \(f\) and \(g\) have the same average order. We will see, for example, that the average order of \(\tau(n)\) is log \(n\), that of \(\sigma(n)\) is \(\dfrac{\pi ^2}{6} n\) and that of \(\varphi (n)\) is \(\dfrac{6}{\pi ^2} n\).
Let us consider first a purely heuristic argument for obtaining the average value of \(\sigma_k(n)\). The probability that \(r\ |\ n\) is \(\dfrac{1}{r}\) and if \(r\ |\ n\) then \(\dfrac{n}{r}\) contributes \((\dfrac{n}{r})^k\) to \(\sigma_k (n)\). Thus the expected value of \(\sigma_k (n)\) is
\(\begin{array} {rcl} {\dfrac{1}{1} (\dfrac{n}{1})^k} & + & {\dfrac{1}{2} (\dfrac{n}{2})^k + \cdot\cdot\cdot + \dfrac{1}{n} (\dfrac{n}{n})^k} \\ {} & = & {n^k(\dfrac{1}{1^{k + 1}} + \dfrac{1}{2^{k + 1}} + \cdot\cdot\cdot + \dfrac{1}{n^{k + 1}})} \end{array}\)
For \(k = 0\) this will be about \(n \text{log } n\). For \(n \ge 1\) it will be about \(n^k \zeta (k + 1)\), e.g., for \(n = 1\) it will be about \(n \zeta(2) = n \dfrac{\pi ^2}{6}\).
Before proceeding to the proof and refinement of some of these results we consider some applications of the inversion of order of summation in certain double sums.
Let \(f\) be an arithmetic function and associate with it the function
\(F(n) = \sum_{d = 1}^{n} f(d)\)
and \(g = f \times I\), i.e.,
\(g(n) = \sum_{d|n} f(d).\)
We will obtain two expressions for
\(\mathcal{F} (x) = \sum_{n = 1}^{x} g(n)\).
\(\mathcal{F}(x)\) is the sum
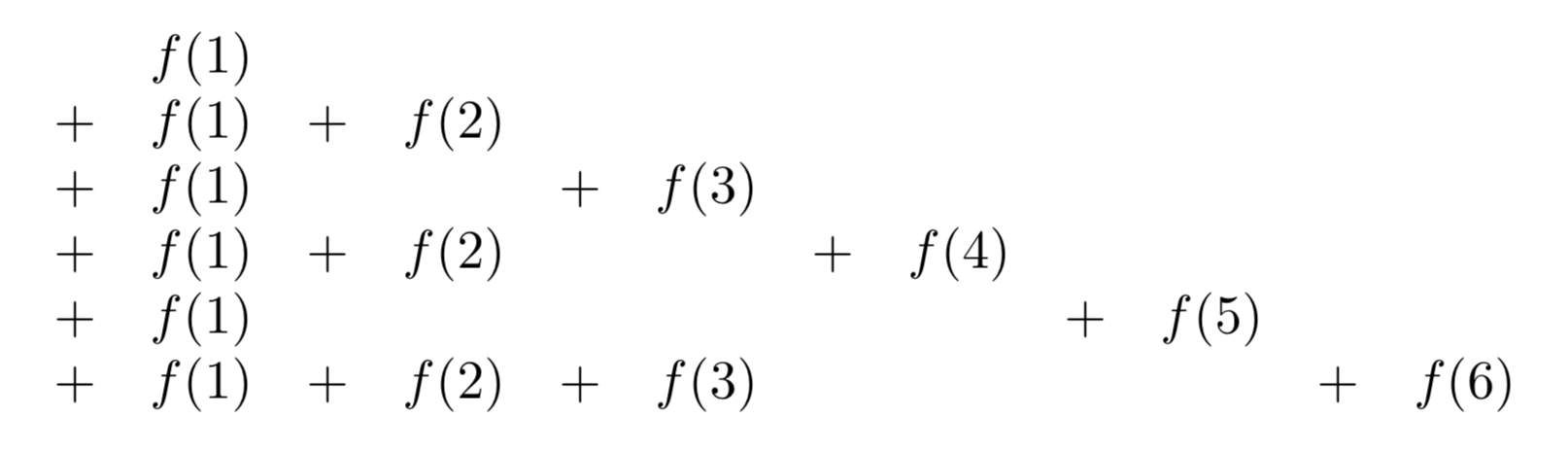
Adding along vertical lines we have
\(\sum_{d = 1}^{x} [\dfrac{x}{d}] f(d)\);
if we add along the successive diagonal lines each beginning with \(f(1)\) and with “slopes” −1, −2, −3, . . . , we obtain
\(\sum_{n = 1}^{x} F([\dfrac{x}{n}]).\)
Thus
\(\sum_{n = 1}^{x} \sum_{d|n} f(d) = \sum_{d = 1}^x [\dfrac{x}{d}] f(d) = \sum_{n = 1}^x F([\dfrac{x}{n}]).\)
The special case \(f = \mu\) yields
\(1 = \sum_{d = 1}^{x} \mu(d) [\dfrac{x}{d}] = \sum_{n = 1}^{x} M([\dfrac{x}{n}]),\)
which we previously considered.
From
\(\sum_{d = 1}^x \mu(d) [\dfrac{x}{d}] = 1\),
we have, on removing brackets, allowing for error, and dividing by \(x\),
\(|\sum_{d = 1}^{x} \dfrac{\mu(d)}{d}| < 1\).
Actually, it is known that
\(\sum_{d = 1}^{\infty} \dfrac{\mu(d)}{d} = 0\),
but a proof of this is as deep as that of the prime number theorem.
Next we consider the case \(f = 1\). Here we obtain
\(\sum_{n = 1}^{x} \tau(n) = \sum_{n = 1}^{x} [\dfrac{x}{n}] = x \log x+ O(x)\).
In the case \(f = I_k\) we find that
\(\sum_{n = 1}^{x} \sigma_k (n) = \sum_{d = 1}^{x} d^k [\dfrac{x}{d}] = \sum_{n = 1}^{x} (1^k + 2^k + \cdot\cdot\cdot + [\dfrac{x}{n}])\).
In the case \(f = \varphi\), recalling that \(\sum_{d|n} \varphi (d) = n\), we obtain
\(\dfrac{x(x + 1)}{2} = \sum_{n = 1}^{x} \sum_{d |n} \varphi (d) = \sum_{d = 1}^{x} [\dfrac{x}{d}] \varphi (d) = \sum_{n = 1}^{x} \Phi (\dfrac{x}{n})\),
where \(\Phi (n) = \sum_{d = 1}^{n} \varphi (d)\). From this we easily obtain
\(\sum_{d = 1}^{x} \dfrac{\varphi (d)}{d} \ge \dfrac{x + 1}{2}\),
which reveals that, on the average, \(\varphi (d) > \dfrac{d}{2}\).
One can also use a similar inversion of order of summation to obtain the following important second M\(\ddot{o}\)bius inversion formula:
Theorem
If \(G(x) = \sum_{n = 1}^{x} F([\dfrac{x}{n}])\) then \(F(x) = \sum_{n = 1}^{x} \mu(n) G([\dfrac{x}{n}]).\)
- Proof
-
\(\begin{array} {rcl} {\sum_{n = 1}^{x} \mu(n) G([\dfrac{x}{n}])} &= & {\sum_{n = 1}^{x} \mu(n) \sum_{n = 1}^{[x/n]} F([\dfrac{x}{mn}])} \\ {} & = & {\sum_{k = 1}^{x} F([\dfrac{x}{n}]) \sum_{n |k}^{x} \mu (n) = F(x).} \end{array}\)
Consider again our estimate
\(\tau (1) + \tau(2) + \cdot\cdot\cdot + \tau(n) = n \log n + O(n).\)
It is useful to obtain a geometric insight into this result. Clearly \(\tau(r)\) is the number of lattice points on the hyperbola \(xy = r\), \(x > 0\), \(y > 0\). Also, every lattice point \((x, y)\), \(x > 0\), \(y > 0\), \(xy \le n\), lies on some hyperbola \(xy = r\), \(r \le n\). Hence
\(\sum_{n = 1}^{n} \tau(r)\)
is the number of lattice points in the region \(xy \le n\), \(x > 0\), \(y > 0\). If we sum along vertical lines \(x = 1, 2, ..., n\) we obtain again
\(\tau(1) + \tau (2) + \cdot\cdot\cdot \tau(n) = [\dfrac{n}{1}] + [\dfrac{n}{2}] + \cdot\cdot\cdot + [\dfrac{n}{n}]\).
In this approach, the symmetry of \(xy = n\) about \(x = y\) suggests how to improve this estimate and obtain a smaller error term.

Using the symmetry of the above figure, we have, with \(u = [\sqrt{n}]\) and \(h(n) = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdot\cdot\cdot + \dfrac{1}{n}\),
\(\begin{array} {rcl} {\sum_{r = 1}^{n} \tau(r)} &= & {2([\dfrac{n}{1}] + \cdot\cdot\cdot + [\dfrac{n}{u}]) - u^2} \\ {} &= & {2nh(u) - n + O(\sqrt{n})} \\ {} &= & {2n \log \sqrt{u} + (2 \gamma - 1)n + O(\sqrt{n})} \\ {} &= & {n \log n + (2 \gamma - 1)n + O(\sqrt{n}).} \end{array}\)
Proceeding now to \(\sum \sigma (r)\) we have
\(\sigma(1) + \sigma (2) + \cdot\cdot\cdot \sigma(n) = 1\ [\dfrac{n}{1}] + 2\ [\dfrac{n}{2}] + \cdot\cdot\cdot n\ [\dfrac{n}{n}].\)
In order to obtain an estimate of \(\sum_{n = 1}^{x} \sigma (n)\) set \(k = 1\) in the identity (obtained earlier)
\(\sigma_k(1) + \sigma_k (2) + \cdot\cdot\cdot \sigma_k (x) = \sum_{n = 1}^{x} (1^k + 2^k + \cdot\cdot\cdot + [\dfrac{x}{n}]^k).\)
We have immediately
\(\begin{array} {rcl} {\sigma (1) + \sigma (2) + \cdot\cdot\cdot \sigma (x)} & = & {\dfrac{1}{2} \sum_{n = 1}^{x} [\dfrac{x}{n}] [\dfrac{x}{n} + 1]} \\ {} & = & {\dfrac{1}{2} \sum_{n = 1}^{\infty} \dfrac{x^2}{n^2} + O(x \log x) = \dfrac{x^2 \zeta (2)}{2} + O(x \log x)} \\ {} & = & {\dfrac{\pi^2 x^2}{12} + O(x \log x).} \end{array}\)
To obtain similar estimates for \(\varphi (n)\) we note that \(\varphi (r)\) is the number of lattice points that lie on the line segment \(x = r\), \(0 < y < r\), and can be seen from the origin. (A point (\(x, y\)) can be seen if \((x, y) = 1\).) Thus \(\varphi (1) + \varphi(2) + \cdot\cdot\cdot + \varphi (n)\) is the number of visible lattice points in the region with \(n > x > y > 0\).
Let us consider a much more general problem, namely to estimate the number of visible lattice points in a large class of regions.
Heuristically we may argue as follows. A point \((x, y)\) is invisible by virtue of the prime \(p\) if \(p\ |\ x\) and \(p\ |\ y\). The probability that this occurs is \(\dfrac{1}{p^2}\). Hence the probability that the point is invisible is
\(\prod_p (1 - \dfrac{1}{p^2}) = \prod_p (1 + \dfrac{1}{p^2} + \dfrac{1}{p^4} + \cdot\cdot\cdot)^{-1} = \dfrac{1}{\zeta (2)} = \dfrac{6}{\pi^2}.\)
Thus the number of visible lattice point should be \(\dfrac{6}{\pi^2}\) times the area of theπ region. In particular the average order of \(\varphi(n)\) should be about \(\dfrac{6}{\pi^2} n\).
We now outline a proof of the fact that in certain large regions the fraction of visible lattice points contained in the region is approximately \(\dfrac{6}{\pi^2}\).
Le \(R\) be a region in the plane having finite Jordan measure and finite perimeter. Let \(tR\) denote the region obtained by magnifying \(R\) radially by \(t\). Let \(M (tR)\) be the area of \(tR\), \(L(tR)\) the number of lattice points in \(tR\), and \(V (tR)\) the number of visible lattice points in \(tR\).
It is intuitively clear that
\(L(tR) = M(tR) + O(t)\) and \(M(tR) = t^2 M(R)\).
Applying the inversion formula to
\(L(tR) = V(tR) + V(\dfrac{t}{2} R) + V(\dfrac{t}{3} R) + \cdot\cdot\cdot\)
we find that
\(\begin{array} {V(tR)} & = & {\sum_{d = 1} L(\dfrac{t}{d} R) \mu (d) = \sum_{d = 1} M(\dfrac{t}{d} R) \mu (d)} \\ {} & \approx & {M(tR) \sum_{d = 1} \dfrac{\mu (d)}{d^2} \approx M(tR) \dfrac{6}{\pi^2} = t^2 M(R) \dfrac{6}{\pi^2}.} \end{array}\)
With \(t = 1\) and \(R\) the region \(n > x > y > 0\), we have
\(\varphi (1) + \varphi (2) + \cdot\cdot\cdot \varphi(n) \approx \dfrac{n^2}{2} \cdot \dfrac{6}{\pi^2} = \dfrac{3}{\pi^2} n^2\)
It has been shown (Chowla) that the error term here cannot be reduced to \(O(n \log \log \log n)\). Walfitz has shown that it can be replaced by \(O(n \log ^{\dfrac{3}{4}} n)\).
Erd\(ddot{o}\)s and Shapiro have shown that
\(\varphi(1) + \varphi (2) + \cdot\cdot\cdot \varphi(n) - \dfrac{3}{\pi^2} n^2\)
changes sign infinitely often.
We will later make an application of our estimate of \(\varphi(1) + \varphi (2) + \cdot\cdot\cdot \varphi(n)\) to the theory of distributions of quadratic residues.
Our result can also be interpreted as saying that if a pair of integers \((a, b)\)
are chosen at random the probability that they will be relatively prime is \(\dfrac{6}{\pi^2}\).
At this stage we state without proof a number of related results.
At this stage we state without proof a number of related results.
If \((a, b)\) are chosen at random the expected value of \((a, b)\) is \(\dfrac{\pi^2}{6}\).
If \(f(x)\) is one of a certain class of arithmetic functions that includes \(x^{\alpha}\), \(0 < \alpha < 1\), then the probability that \((x, f(x)) = 1\) is \(\dfrac{6}{\pi^2}\), and its expected value is \(\dfrac{\pi^2}{6}\).
This and related results were proved by Lambek and Moser.
The probability that \(n\) numbers chosen at random are relatively prime is \(\dfrac{1}{\zeta(n)}\).
The number \(Q(n)\) of quadratfrei numbers under \(n\) is \(\thicksim \dfrac{6}{\pi^2} n\) and the number \(O_k (n)\) of \(k\)th power-free numbers under \(n\) is \(\dfrac{n}{\zeta(k)}.\) The first result follows almost immediately from
\(\sum Q (\dfrac{n^2}{r^2}) = n^2,\)
so that by the inversion formula
\(Q(n^2) = \sum \mu(r) [\dfrac{n}{r}]^2 \thicksim n^2 \zeta (2).\)
A more detailed argument yields
\(Q(x) = \dfrac{6x}{\pi^2} + O(\sqrt{x}).\)
Another rather amusing related result, the proof of which is left as an exercise, is that
\(\sum_{(a, b) = 1} \dfrac{1}{a^2b^2} = \dfrac{5}{2}.\)
The result on \(Q(x)\) can be written in the form
\(\sum_{n = 1}^{x} |\mu(n)| \thicksim \dfrac{6}{\pi^2} x\)
One might ask for estimates for
\(\sum_{n = 1}^{x} \mu(n) = M(x).\)
Indeed, it is known (but difficult to prove) that \(M(x) = o(x)\).
Let us turn out attention to \(\omega (n)\). We have
\(\omega(1) + \omega(2) + \cdot\cdot\cdot \omega(n) = \sum_{p \le n} [\dfrac{n}{p}] \thicksim n\log \log n\).
Thus the average value of \(\omega(n)\) is log log \(n\).
The same follows in a similar manner for \(\Omega (n)\)
A relatively recent development along these lines, due to Erd\(\ddot{o}\)s, Kac, Leveque, Tatuzawa and others is a number of theorems of which the following is typical.
Let \(A(x; \alpha, \beta)\) be the number of integers \(n \le x\) for which
\(\alpha \sqrt{\log \log n} + \log \log n < \omega (n) < \beta \sqrt{\log \log n} + \log \log n.\)
Then
\(\text{lim}_{x \to \infty} \dfrac{A(x; \alpha, \beta)}{x} = \dfrac{1}{\sqrt{2\pi}} \int_{\alpha}^{\beta} e^{-\dfrac{u^2}{2}} du.\)
Thus we have for example that \(\omega (n) < \log \log n \) about half the time.
One can also Prove (Tatuzawa) that a similar result holds for \(B(x; \alpha, \beta)\), the number of integers in the set \(f(1)\), \(f(2)\), ..., \(f(x)\) (\(f(x)\) is an irreducible polynomial with integral coefficients) for which \(\omega (f(n))\) lies in a range similar to those prescribed for \(\omega(n)\).
Another type of result that has considerable applicability is the following.
The number \(C(x, \alpha)\) of integers \(\le x\) having a prime divisor \(> x \alpha\), \(1 > \alpha > \dfrac{1}{2}\), is \(\thicksim -x \log \alpha\). In fact, we have
\(\begin{array} {rcl} {C(x, \alpha)} & = & {\sum_{x^{alpha} < p < x} \dfrac{x}{p} \thicksim x \sum_{x^{alpha} < p x} \dfrac{1}{p}} \\ {} & = & {x (\log \log x - \log \log \alpha)} \\ {} & = & {x (\log \log x - \log \log x - \log \alpha) = - x \log \alpha.} \end{array}\)
For example the density of numbers having a prime factor exceeding their square root is log 2 \(\approx\).7.
Thus far we have considered mainly average behavior of arithmetic functions. We could also inquire about absolute bounds. One can prove without difficulty that
\(1 > \dfrac{varphi(n) \sigma(n)}{n^2} > \epsilon > 0\) for all \(n\).
Also, it is known that
\(n > \varphi(n) > \dfrac{cn}{\log\log n}\)
and
\(n < \sigma(n) < cn \log\log n.\)
As for \(\tau(n)\), it is not difficult to show that
\(\tau (n) > (\log n)^k\)
infinitely often for every \(k\) while \(\tau(n) < n^{\epsilon}\) for every \(\epsilon\) and \(n\) sufficient large.
We state but do not prove the main theorem along these lines.
If \(\epsilon > 0\) then
\(\tau(n) < 2^{(1 + \epsilon) \log n / \log \log n}\) for all \(n > n_0(\epsilon)\)
while
\(\tau(n) > 2^{(1 - \epsilon) \log n / \log \log n}\) infinitely often.
A somewhat different type of problem concerning average value of arithmetic functions was the subject of a University of Alberta master’s thesis of Mr. R. Trollope a couple of years ago.
Let \(s_r(n)\) be the sum of the digits of n when written in base \(r\). Mirsky has proved that
\(s_r(1) + s_r(2) + \cdot \cdot \cdot + s_r(n) = \dfrac{r - 1}{2} n \log_r n + O(n).\)
Mr. Trollope considered similar sums where the elements on the left run over certain sequences such as primes, squares, etc.
Still another quite amusing result he obtained states that
\(\dfrac{s_1(n) + s_2(n) + \cdot\cdot\cdot s_n(n)}{n^2} \thicksim 1 - \dfrac{\pi^2}{12}.\)


