4.1: An Introduction to Sets
- Page ID
- 8400
A set is a collection of objects. The objects in a set are called its elements or members. The elements in a set can be any types of objects, including sets! The members of a set do not even have to be of the same type. For example, although it may not have any meaningful application, a set can consist of numbers and names.
We usually use capital letters such as \(A\), \(B\), \(C\), \(S\), and \(T\) to represent sets, and denote their generic elements by their corresponding lowercase letters \(a\), \(b\), \(c\), \(s\), and \(t\), respectively. To indicate that \(b\) is an element of the set \(B\), we adopt the notation \(b\in B\), which means “ \(b\) belongs to \(B\)” or “ \(b\) is an element of \(B\).” We also write \(B\mathbb{N}i b\), and say “ \(B\) contains \(b\) (as an element).”
We designate these notations for some special sets of numbers: \[\begin{array}{c c l} \mathbb{R} &=& \mbox{the set of real numbers}, \\ \mathbb{Q} &=& \mbox{the set of rational numbers}, \\ \mathbb{Z} &=& \mbox{the set of integers}, \\ \mathbb{N} &=& \mbox{the set of natural numbers (positive integers)}. \end{array} \nonumber\] All these are infinite sets, because they all contain infinitely many elements. In contrast, finite sets contain finitely many elements.
We can use the roster method to describe a set if it has only a small number of elements. We list all its elements explicitly, as in \[A = \mbox{the set of natural numbers not exceeding 7} = \{1,2,3,4,5,6,7\}. \nonumber\] For sets with more elements, show the first few entries to display a pattern, and use an ellipsis to indicate “and so on.” For example, \[\{1,2,3,\ldots,20\} \nonumber\] represents the set of the first 20 positive integers. The repeating pattern can be extended indefinitely, as in \[\begin{array}{c c l} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ldots,-2,-1,0,1,2,\ldots\} \end{array} \nonumber\] There are three kinds of integers: positive, negative, and the signless integer zero. In regards to parity, an integer is either even or odd. An integer is even if and only if it is divisible by two. Therefore, the set of even integers can be described as \(\{\ldots,-4,-2,0,2,4,\ldots\}\).
We can use a set-builder notation to describe a set. For example, the set of natural numbers is defined as \[\mathbb{N} = \{x\in\mathbb{Z} \mid x>0 \}. \nonumber\] Here, the vertical bar \(\mid\) is read as “such that” or “for which.” Hence, the right-hand side of the equation is pronounced as “the set of \(x\) belonging to the set of integers such that \(x>0\),” or simply “the set of integers \(x\) such that \(x>0\).” In general, this descriptive method appears in the format \[\{\,\mbox{membership}\;\mid\;\mbox{properties}\,\}. \nonumber\] The notation \(\mid\) means “such that” or “for which” only when it is used in the set notation. It may mean something else in a different context. Therefore, do not write “let \(x\) be a real number \(\mid\) \(x^2>3\)” if you want to say “ let \(x\) be a real number such that \(x^2>3\).” It is considered improper to use a mathematical notation as an abbreviation.
Example \(\PageIndex{1}\label{eg:setintro-01}\)
Write these two sets \[\{x\in\mathbb{Z} \mid x^2 \leq 1\} \quad\mbox{and}\quad \{x\in\mathbb{N} \mid x^2 \leq 1\} \nonumber\] by listing their elements explicitly.
- Answer
-
The first set has three elements, and equals \(\{-1,0,1\}\). The second set is a singleton set; it is equal to \(\{1\}\).
hands-on exercise \(\PageIndex{1}\label{he:setintro-01}\)
Use the roster method to describe the sets \(\{x\in\mathbb{Z} \mid x^2\leq20\}\) and \(\{x\in\mathbb{N} \mid x^2\leq20\}\).
hands-on exercise \(\PageIndex{2}\label{he:setintro-02}\)
Use the roster method to describe the set \[\{x\in\mathbb{N} \mid x\leq20 \mbox{ and $x=n^2$ for some integer $n$}\}. \nonumber\]
There is a slightly different format for the set-builder notation. Before the vertical bar, we describe the form the elements assume, and after the vertical bar, we indicate from where we are going to pick these elements: \[\{\,\mbox{pattern}\;\mid\;\mbox{membership}\,\}. \nonumber\] Here the vertical bar \(\mid\) means “where.” For example, \[\{ x^2 \mid x\in\mathbb{Z} \} \nonumber\] is the set of \(x^2\) where \(x\in\mathbb{Z}\). It represents the set of squares: \(\{0,1,4,9,16,25,\ldots\}\).
Example \(\PageIndex{2}\label{eg:setintro-02}\)
The set \[\{ 2n \mid n\in\mathbb{Z} \} \nonumber\] describes the set of even numbers. We can also write the set as \(2\mathbb{Z}\).
hands-on exercise \(\PageIndex{3}\label{he:setintro-03}\)
Describe the set \(\{2n+1 \mid n\in\mathbb{Z}\}\) with the roster method.
hands-on exercise \(\PageIndex{4}\label{he:setintro-04}\)
Use the roster method to describe the set \(\{3n \mid n\in\mathbb{Z}\}\).
An interval is a set of real numbers, all of which lie between two real numbers. Should the endpoints be included or excluded depends on whether the interval is open, closed, or half-open. We adopt the following interval notation to describe them: \[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a,b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}. \cr} \nonumber\] It is understood that \(a\) must be less than or equal to \(b\). Hence, the notation \((5,3)\) does not make much sense. How about \([3,3]\)? Is it a legitimate notation?
An interval contains not just integers, but all the numbers between the two endpoints. By numbers, we mean whole numbers and decimal numbers. For instance, \((1,5) \neq \{2,3,4\}\) because the interval \((1,5)\) also includes decimal numbers such at \(1.276\), \(\sqrt{2}\), and \(\pi\).
We can use \(\pm\infty\) in the interval notation: \[\begin{array}{r c l} (a,\infty) &=& \{ x\in\mathbb{R} \mid a<x \}, \\ (-\infty,a) &=& \{ x\in\mathbb{R} \mid x<a \}. \end{array} \nonumber\] However, we cannot write \((a,\infty]\) or \([-\infty,a)\), because \(\pm\infty\) are not numbers. It is nonsense to say \(x\leq\infty\) or \(-\infty\leq x\). For the same reason, we can write \([a,\infty)\) and \((-\infty,a]\), but not \([a,\infty]\) or \([-\infty,a]\).
Example \(\PageIndex{3}\label{eg:setintro-03}\)
Write the intervals \((2,3)\), \([2,3]\), and \((2,3]\) in the descriptive form.
- Solution
-
According to the definition of an interval, we find \[\begin{array}{c c l} {(2,3)} &=& \{x\in\mathbb{R} \mid 2<x<3\}, \\ {[2,3]} &=& \{x\in\mathbb{R} \mid 2\leq x\leq 3\}, \\ {(2,3]} &=& \{x\in\mathbb{R} \mid 2 < x\leq 3\}. \end{array} \nonumber\] What would you say about \([2,3)\)?
Example \(\PageIndex{4}\label{eg:setintro-04}\)
Write these sets \[\{x\in\mathbb{R} \mid -2 \leq x < 5\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid x^2 \leq 1\} \nonumber\] in the interval form.
- Solution
-
The answers are \([-2,5)\) and \([-1,1]\), respectively. The membership of \(x\) affects the answers. If we change the second set to \(\{x\in\mathbb{Z} \mid x^2\leq 1\}\), the answer would have been \(\{-1,0,1\}\). Can you explain why \(\{-1,0,1\} \neq [-1,1]\)?
Example \(\PageIndex{5}\label{eg:setintro-05}\)
Be sure you are using the right types of numbers. Compare these two sets \[\begin{array}{c c l} S &=& \{x\in\mathbb{Z} \mid x^2 \leq 5 \}, \\ T &=& \{x\in\mathbb{R} \mid x^2 \leq 5 \}. \end{array} \nonumber\] One consists of integers only, while the other contains real numbers. Thus, \(S=\{-2,-1,0,1,2\}\), and \(T=\big[-\sqrt{5},\sqrt{5}\,\big]\).
hands-on exercise \(\PageIndex{5}\label{he:setintro-05}\)
Which of the following sets \[\{x\in\mathbb{Z} \mid 1<x<7\} \quad\mbox{and}\quad \{x\in\mathbb{R} \mid 1<x<7\} \nonumber\] can be represented by the interval notation \((1,7)\)? Explain.
hands-on exercise \(\PageIndex{6}\label{he:setintro-06}\)
Explain why \([2,7\,] \neq\{2,3,4,5,6,7\}\).
hands-on exercise \(\PageIndex{7}\label{he:setintro-07}\)
True or false: \((-2,3)=\{-1,0,1,2\}\)? Explain.
Let \(S\) be a set of numbers; we define \[\begin{array}{c c l} S^+ &=& \{ x\in S \mid x>0 \}, \\ S^- &=& \{ x\in S \mid x<0 \}, \\ S^* &=& \{ x\in S \mid x \neq 0 \}. \end{array} \nonumber\] In plain English, \(S^+\) is the subset of \(S\) containing only those elements that are positive, \(S^-\) contains only the negative elements of \(S\), and \(S^*\) contains only the nonzero elements of \(S\).
Example \(\PageIndex{6}\label{eg:setintro-06}\)
It should be obvious that \(\mathbb{N}=\mathbb{Z}^+\).
hands-on exercise \(\PageIndex{8}\label{he:setintro-08}\)
What is the notation for the set of negative integers?
Some mathematicians also adopt these notations: \[\begin{aligned} bS &=& \{ bx \mid x\in S \}, \\ a+bS &=& \{ a+bx \mid x\in S \}. \end{aligned} \nonumber\] Accordingly, we can write the set of even integers as \(2\mathbb{Z}\), and the set of odd integers can be represented by \(1+2\mathbb{Z}\).
An empty set is a set that does not contain any element. Both \[\{x\in\mathbb{R} \mid x>0 \mbox{ and } x<0\} \qquad\mbox{and}\qquad \{x\in\mathbb{R} \mid x^2 < 0\} \nonumber\] are examples of empty sets. The second example illustrates a typical application of an empty set. It provides a convenient way of declaring that a problem has no solution: we say that the solution set is an empty set. We denote an empty set with the notation \(\emptyset\) or \(\{\,\}\). For example, can you explain why \((3,3)=\emptyset\)?
hands-on exercise \(\PageIndex{9}\label{he:setintro-09}\)
What does the notation \([7,7\,]\) mean? How would you describe the sets \((7,7)\), \((7,7\,]\) and \([7,7)\)?
Example \(\PageIndex{7}\label{eg:setintro-07}\)
Determine which of these statements are true. \[\begin{aligned} \{x\in\mathbb{R} \mid (x^2+2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{Z} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3) = 0\} &=& \emptyset, \\ \{x\in\mathbb{R} \mid (x^2-2)(x^2+3)\geq0\} &=& \emptyset. \end{aligned} \nonumber\]
- Solution
-
The answers are: true, true, false, and false, respectively.
Example \(\PageIndex{8}\label{eg:setintro-08}\)
When we write \(3,4,5,\ldots,n\), we are referring to a list of integers between 3 and \(n\), inclusive. It is understood that \(n\geq3\). Consequently, the set \[\{3,4,5,\ldots,n\} \nonumber\] is empty when \(n=2\).
Two sets \(A\) and \(B\) are said to be equal if they contain the same collection of elements. More rigorously, we define \[A = B \Leftrightarrow \forall x \, (x \in A \Leftrightarrow x \in B). \nonumber\] Since the elements of a set can themselves be sets, exercise caution and use proper notation when you compare the contents of two sets.
Example \(\PageIndex{9}\label{eg:setintro-09}\)
Explain why \(\big\{0,\{1\}\big\} \neq \{0,1\}\).
- Solution
-
The set \(\big\{0,\{1\}\big\}\) consists of two elements: the integer \(0\) and the set \(\{1\}\). The set \(\{0,1\}\) also consists of two elements, both of them integers; namely, 0 and 1.
You may find the following analogy helpful. Imagine a set being a box. You open a box to look at its contents. The box itself can be compared to the curly braces \(\{\) and \(\}\). What it holds is exactly what we call the elements of the set it represents. The contents of the two sets \(\big\{0,\{1\}\big\}\) and \(\{0,1\}\) are depicted in the boxes shown in Figure \(\PageIndex{1}\).
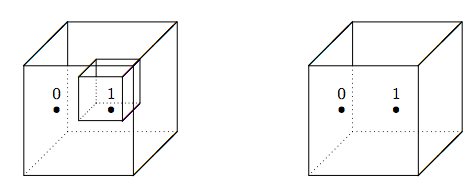
Figure \(\PageIndex{1}\): The two sets \(\big\{0,\{1\}\big\}\) and \({0,1}\). When you open the first box, you find two items. One of them is the number 0; the other is another box that contains the number 1. The second box also contains two items that are both numbers. What you find in these two boxes is not the same. Hence, the sets they represent are different.
hands-on exercise \(\PageIndex{10}\label{he:setintro-10}\)
Name some differences between the sets \(\big\{0,\{1\}\big\}\) and \(\big\{\{0\},\{1\}\big\}\).
Example \(\PageIndex{10}\label{eg:setintro-10}\)
True or false: \(\mathbb{Z}=\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\}\big\}\)?
- Solution
-
The set on the left is \(\mathbb{Z}\), and \[\mathbb{Z} = \{\ldots,-3,-2,-1,0,1,2,3,\ldots\}. \nonumber\] It is an infinite set. The set on the right consists of only three elements:
- the set \(\{\ldots,-3,-2,-1\}\), which is the set of negative integers,
- the integer 0, and
- the set \(\{1,2,3,\ldots\}\), which is the set of positive integers.
Hence, they are not equal. Notice that \[\mathbb{Z} \neq \big\{\{\ldots,-3,-2,-1\}, \{0\}, \{1,2,3,\ldots\}\big\} \nonumber\] either, because the set on the right is a set of three sets, while the set on the left is a set of integers. One has three elements; the other has infinitely many elements.
To reduce confusion, instead of saying a set of sets, we could say a collection of sets or a family of sets. For example, \[\big\{\{1,3,5,\ldots,\}, \{2,4,6,\ldots\,\}\big\} \nonumber\] is a family of two sets, one of which is the set of positive odd integers; the other is the set of positive even integers.
Definition
A set is said to be finite if it has a finite number of elements. The number of elements in a finite set \(A\) is called its cardinality, and is denoted by \(|A|\). Hence, \(|A|\) is always nonnegative. If \(A\) is an infinite set, some authors would write \(|A|=\infty\).
Example \(\PageIndex{11}\label{eg:setintro-11}\)
While it is trivial that \(|\{1,4,7,8\}| = 4\), and \(|\{0,1\}| = 2\), it may not be obvious that \[\big|\big\{0,\{1\}\big\}\big| = 2, \nonumber\] and \[\big|\big\{\{\ldots,-3,-2,-1\},0,\{1,2,3,\ldots\,\}\big\}| = 3. \nonumber\] What matters is the number of entries in a set, which can be compared to how many items you can find when you open a box. Here is another example: \[|\{x\in\mathbb{R} \mid x^2=9\}| = 2 \nonumber\] because the equation \(x^2=9\) has two real solutions. What is \(|\{x\in\mathbb{N} \mid x^2=9\}|\)?
hands-on exercise \(\PageIndex{11}\label{he:setintro-11}\)
Determine these cardinalities:
- \(|\{x\in\mathbb{Z} \mid x^2-7x-6=0\}|\)
- \(|\{x\in\mathbb{R} \mid x^2-x-12<0\}|\)
- \(|\{x\in\mathbb{Z} \mid \mbox{ x is prime and x is even}\}|\)
Recall that your answers should be nonnegative.
hands-on exercise \(\PageIndex{12}\label{he:setintro-12}\)
Explain why it is incorrect to say \(|\emptyset|=\emptyset\). In fact, it is nonsense to say \(|\emptyset|=\emptyset\). Explain. What should be the value of \(|\emptyset|\)?
We close this section with an important remark about sets. It follows from the definition of equality of sets that we do not count repeated elements as separate elements. For example, suppose a small student club has three officers:
| chair: | Mary, |
| vice chair: | John, |
| secretary: | John; |
and let \(A\) represent the set of its officers, and \(B\) the set of positions in its executive board, then \(|A|=2\) and \(|B|=3\), because \[A = \{ \mbox{Mary}, \mbox{John} \}, \nonumber\] and \[B = \{ \mbox{chair}, \mbox{vice chair}, \mbox{secretary}\}. \nonumber\]
Example \(\PageIndex{12}\label{eg:setintro-12}\)
Find the errors in the following statement: \[|\{-2,2\}| = \{\,|-2|,|2|\} = \{2\} = 2, \nonumber\] and correct them.
- Solution
-
This statement contains several errors. The first mistake is assuming that we can distribute the “absolute value” symbols \(|\quad|\) over the contents of a set: \[|\{-2,2\}| \neq \{\,|-2|,|2|\}. \nonumber\] After all, the two vertical bars do not mean absolute value in this case. Instead, it means the cardinality of the set \(\{-2,2\}\). Hence, \(|\{-2,2\}|=2\).
The second equality \(\{\,|-2|,|2|\} = \{2\}\) is correct. After taking absolute values, both entries become 2. However, we do not write \(\{|-2|,|2|\} = \{2,2\}\), because a set should not contain repetition. Therefore, it is correct to say \(\{\,|-2|,|2|\} = \{2\}\).
The last equality \(\{2\}=2\) is wrong. We cannot compare a set to a number. Imagine the set \(\{2\}\) as a box containing only one object, and that object is the number 2. In contrast, 2 on the right-hand side is left in the open air without any containment. It is clear that \(\{2\} \neq 2\).
The entire statement contains multiple mistakes; some of them are syntactical errors while some are conceptual. Nevertheless, we do have \(|\{-2,2\}|=2\). Although the final answer is correct, the argument used to obtain it is not.
In some situations, we do want to count repeated elements as separate elements, as in \(S=\{1,2,2,2,3,3,4,4\}\). We call such a collection a multiset instead of an ordinary set. In this case, \(|S|=8\).
Summary and Review
- A set is a collection of objects (without repetitions).
- To describe a set, either list all its elements explicitly, or use a descriptive method.
- Intervals are sets of real numbers.
- The elements in a set can be any type of object, including sets.
- We can even have a set containing dissimilar elements. In particular, we can mix elements and sets inside a set.
- If a set \(A\) is finite, its cardinality \(|A|\) is the number of elements it contains. Consequently, \(|A|\) is always nonnegative.
Exercises 4.1
Exercise \(\PageIndex{1}\label{ex:setintro-01}\)
Write each of these sets by listing its elements explicitly (that is, using the roster method).
- \(\{n\in\mathbb{Z} \mid -6<n<4\}\)
- \(\{n\in\mathbb{N} \mid -6<n<4\}\)
- \(\{x\in\mathbb{Q} \mid x^3-x^2-6x=0\}\)
- \(\{x\in\mathbb{Q} \mid x^4-11x^2+18=0\}\).
Exercise \(\PageIndex{2}\label{ex:setintro-02}\)
Use the roster method to describe these sets:
- \(\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 }\}\)
- \(\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 or a multiple of 5 }\}\)
- \(\{x\in\mathbb{Z} \mid \mbox{ |x|<20 and x is a multiple of 3 and a multiple of 5}\}\)
- \(\{x\in\mathbb{N} \mid \mbox{ x<20 and x is a multiple of 3 but not a multiple of 5}\}\)
Exercise \(\PageIndex{3}\label{ex:setintro-03}\)
Write each of the following sets in the form \(\{n\in\mathbb{Z} \mid p(n)\}\) with a logical statement \(p(n)\) describing the property of \(n\).
- \(\{\ldots,-3,-2,-1\}\)
- \(\{\ldots,-27,-8,-1,0,1,8,27,\ldots\}\)
- \(\{0,1,4,9,16,\ldots\}\)
- \(\{\ldots,-15,-10,-5,0,5,10,15,\ldots\}\)
- \(\{0,4,8,12,\ldots\}\)
- \(\{\ldots,-14,-8,-2,4,10,16,\ldots\}\)
Exercise \(\PageIndex{4}\label{ex:setintro-04}\)
Repeat the previous problem, but write the sets in the form \(\{ f(n) \mid n\in S\}\), where \(f(n)\) is a formula that describes the pattern of the elements, and \(S\) is an appropriate set of numbers.
Exercise \(\PageIndex{5}\label{ex:setintro-05}\)
Whenever possible, express the sets in Problem 3 in the form \(S^+\), \(S^-\), \(bS\), or \(a+bS\) for some appropriate set \(S\).
Exercise \(\PageIndex{6}\label{ex:setintro-06}\)
Determine whether the following sets are empty, finite sets, or infinite sets:
- \(\{2n+1 \mid n\in\mathbb{N}\}\)
- \(\{x\in\mathbb{R} \mid x^2<0\}\)
- \(\{x\in\mathbb{Q} \mid x\geq0 \mbox{ and } x\leq0\}\)
- \(\{x\in\mathbb{N} \mid x<0 \mbox{ or } x>0\}\)
Exercise \(\PageIndex{7}\label{ex:setintro-07}\)
Write each of these sets in the interval notation.
- \(\{x\in\mathbb{R} \mid -4<x<7\}\)
- \(\{x\in\mathbb{R} \mid -4<x\leq7\}\)
- \(\{x\in\mathbb{R}^+\mid -4<x\leq7\}\)
- \(\{x\in\mathbb{R} \mid -4<x\}\)
- \(\{x\in\mathbb{R} \mid x\leq6\}\)
- \(\{x\in\mathbb{R}^-\mid 0\leq x\leq6\}\)
Exercise \(\PageIndex{8}\label{ex:setintro-08}\)
Is \([-\infty,\infty]\) a legitimate or correct notation? Explain.
Exercise \(\PageIndex{9}\label{ex:setintro-09}\)
Evaluate the following expressions.
- \(|\{x\in\mathbb{Z} \mid -4<x<7\}|\)
- \(|\{x\in\mathbb{Z} \mid -4<x\leq7\}|\)
- \(|\{x\in\mathbb{N} \mid -4<x\leq7\}|\)
- \(|\{x\in\mathbb{R} \mid x^4-2x^3-35x^2=0\}|\)
- \(|\{-3,-2,2,3\}|\)
- \(|\{x\in\mathbb{Q} \mid x^2=3\}|\)
Exercise \(\PageIndex{10}\label{ex:setintro-10}\)
Determine which of the following statements are true, and which are false.
- \(a\in\{a\}\)
- \(\{3,5\}=\{5,3\}\)
- \(\emptyset\in\emptyset\)
- \(\emptyset=\{\emptyset\}\)
- \(\{\;\}=\emptyset\)
- \(\emptyset\in\{\emptyset\}\)
Exercise \(\PageIndex{11}\label{ex:setintro-11}\)
Determine which of the following statements are true, and which are false.
- \(2\in(2,7)\)
- \(\sqrt{2}\in(1,3)\)
- \(\big(\sqrt{5}\,\big)^2\in\mathbb{Q}\)
- \(-5\in\mathbb{N}\)
Exercise \(\PageIndex{12}\label{ex:setintro-12}\)
Give examples of sets \(A\), \(B\) and \(C\) such that:
- \(A\in B\) and \(B\in C\), and \(A \notin C\)
- \(A\in B\) and \(B\in C\), and \(A\in C\)
Exercise \(\PageIndex{13}\label{ex:setintro-13}\)
Determine whether the following statements are correct or incorrect syntactically. For those that are syntactically correct, determine their truth values; for those that are syntactically incorrect, suggest ways to fix them.
- \((3,7\,]=3<x\leq7\).
- \(\{x\in\mathbb{R}\mid x^2<0\} \equiv \emptyset\).
Exercise \(\PageIndex{14}\label{ex:setintro-14}\)
Determine whether the following statements are correct or incorrect syntactically. For those that are syntactically correct, determine their truth values; for those that are syntactically incorrect, suggest ways to fix them.
- \(\frac{7}{4}\in[2,\sqrt{7})\).
- There does not exist \(x\) such that \(x\in\mathbb{R}^+\) and \(\mathbb{R}^-\).
- If \((0,\infty)\), then \(x\) is positive.


