6.3: One-to-One Functions
- Page ID
- 8416
We distinguish two special families of functions: the one-to-one functions and the onto functions. We shall discuss one-to-one functions in this section, and onto functions in the next.
Definition: Injection
A function \({f}:{A}\to{B}\) is said to be one-to-one if
\[x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2) \nonumber\]
for all elements \(x_1,x_2\in A\). A one-to-one function is also called an injection, and we call a function injective if it is one-to-one. A function that is not one-to-one is referred to as many-to-one.
Any well-defined function is either one-to-one or many-to-one. A function cannot be one-to-many because no element can have multiple images. The difference between one-to-one and many-to-one functions is whether there exist distinct elements that share the same image. There are no repeated images in a one-to-one function.
Example \(\PageIndex{1}\label{eg:oneonefcn-01}\)
The identity function on any nonempty set \(A\) \[{i_A}:{A}\to{A}, \qquad i_A(x)=x, \nonumber\] maps any element back to itself. It is clear that all identity functions are one-to-one.
Example \(\PageIndex{2}\label{eg:oneonefcn-02}\)
The function \( h : {A}\to{A}\) defined by \(h(x)=c\) for some fixed element \(c\in A\), is an example of a constant function. It is a function with only one image. This is the exact opposite of an identity function. It is clearly not one-to-one unless \(|A|=1\).
For domains with a small number of elements, one can use inspection on the images to determine if the function is one-to-one. This becomes impossible if the domain contains a larger number of elements.
In practice, it is easier to use the contrapositive of the definition to test whether a function is one-to-one:
\[f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \nonumber\]
Example \(\PageIndex{3}\label{eg:oneonefcn-03}\)
Is the function \( f : {\mathbb{R}}\to{\mathbb{R}}\) defined by \(f(x)=3x+2\) one-to-one?
- Solution
-
Assume \(f(x_1)=f(x_2)\), which means \[3x_1+2 = 3x_2+2. \nonumber\] Thus \(3x_1=3x_2\), which implies that \(x_1=x_2\). Therefore \(f\) is one-to-one.
exercise \(\PageIndex{1}\label{he:oneonefcn-01}\)
Determine whether the function \( g : {\mathbb{R}}\to{\mathbb{R}}\) defined by \(g(x)=5-7x\) is one-to-one.
exercise \(\PageIndex{2}\label{he:oneonefcn-02}\)
Determine whether the function \( h : {[2,\infty)}\to{\mathbb{R}}\) defined by \(h(x)=\sqrt{x-2}\) is one-to-one.
Interestingly, sometimes we can use calculus to determine if a real function is one-to-one. A real function \(f\) is increasing if \[x_1 < x_2 \Rightarrow f(x_1) < f(x_2), \nonumber\] and decreasing if \[x_1 < x_2 \Rightarrow f(x_1) > f(x_2). \nonumber\] Obviously, both increasing and decreasing functions are one-to-one. From calculus, we know that
- A function is increasing over an open interval \((a,b)\) if \(f'(x)>0\) for all \(x\in(a,b)\).
- A function is decreasing over an open interval \((a,b)\) if \(f'(x)<0\) for all \(x\in(a,b)\).
Therefore, if the derivative of a function is always positive, or always negative, then the function must be one-to-one.
Example \(\PageIndex{4}\label{eg:oneonefcn-04}\)
The function \(p : {\mathbb{R}}\to{\mathbb{R}}\) defined by \[p(x) = 2x^3-5 \nonumber\] is one-to-one, because \(p'(x)=6x^2>0\) for any \(x\in\mathbb{R}^*\). Likewise, the function \(q:{\big(-\frac{\pi}{2},\frac{\pi}{2}\big)}\to{\mathbb{R}}\) defined by \[q(x) = \tan x \nonumber\] is also one-to-one, because \(q'(x) = \sec^2x > 0\) for any \(x\in \big(-\frac{\pi}{2},\frac{\pi}{2}\big)\).
exercise \(\PageIndex{3}\label{he:oneonefcn-03}\)
Use both methods to show that the function \(k:{(0,\infty)}\to{\mathbb{R}}\) defined by \(k(x) = \ln x\) is one-to-one.
Example \(\PageIndex{5}\label{eg:oneonefcn-05}\)
The function \( h : {\mathbb{R}}\to{\mathbb{R}}\) given by \(h(x)=x^2\) is not one-to-one because some of its images are identical. For example, \(h(3) = h(-3) =9\). It is a many-to-one function. Likewise, the absolute value function \(|x|\) is not one-to-one.
The functions \(p:{[\,0,\infty)}\to{\mathbb{R}}\) defined by \(p(x)=x^2\) and \(q:{[\,0,\infty)}\to{\mathbb{R}}\) defined by \(q(x)=|x|\) are one-to-one. Whether a function is one-to-one depends not only on its formula, but also on its domain. Consequently, sometimes we may be able to convert a many-to-one function into a one-to-one function by modifying its domain.
Example \(\PageIndex{6}\label{eg:onetoone}\)
Construct a one-to-one function from \([\,1,3\,]\) to \([\,2,5\,]\).
- Solution
-
There are many possible solutions. In any event, start with a graph. We can use a straight line graph. The domain \([\,1,3\,]\) lies on the \(x\)-axis, and the codomain \([\,2,5\,]\) lies on the \(y\)-axis. Hence the graph should cover the boxed region in Figure \(\PageIndex{1}\).
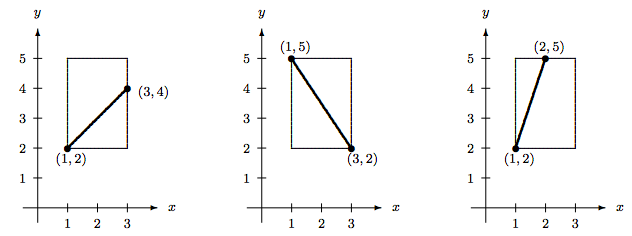
Figure \(\PageIndex{1}\): Three candidates for one-to-one functions from [1,3] to [2,5]. All three graphs do not produce duplicate images. We need to cover all \(x\)-values from 1 to 3 in order for the function to be well-defined. This leaves only the first two graphs as legitimate examples.
To determine the formula for \(f\), we need to derive the equation of the line. Take the first graph as our choice. The line joins the point \((1,2)\) to the point \((3,4)\). Thus, its equation is \[\frac{y-2}{x-1} = \frac{4-2}{3-1} = 1. \nonumber\] The last step is to write the answer in the form of \(f(x)=\ldots\,\). We have to express \(y\) in terms of \(x\). We find \(y = x+1\). Hence, \[ f : {[\,1,3\,]}\to{[\,2,5\,]}, \qquad f(x) = x+1 \nonumber\] is an example of a one-to-one function.
exercise \(\PageIndex{4}\label{he:oneonefcn-04}\)
Construct a one-to-one function from \([\,1,3\,]\) to \([\,2,5\,]\) based on the second graph in Example 6.3.6.
exercise \(\PageIndex{5}\label{he:oneonefcn-05}\)
Construct a one-to-one function from \([\,3,8\,]\) to \([\,2,5\,]\).
example \(\PageIndex{7}\label{eg:gmod43}\)
Determine whether the function \( g : {\mathbb{Z}_{43}}\to{\mathbb{Z}_{43}}\) defined by \[g(x) \equiv 11x-5 \pmod{43} \nonumber\] is one-to-one.
- Solution
-
Assume \(g(x_1)=g(x_2)\). This means \[11x_1 - 5 \equiv 11x_2 - 5 \pmod{43}, \nonumber\] which implies \[11x_1 \equiv 11x_2 \pmod{43}. \nonumber\] Notice that \(4\cdot11=44\equiv1\) (mod 43), hence \(11^{-1}\equiv4\) (mod 43). Multiplying 4 to both sides of the last congruence yields \[44 x_1 \equiv 44 x_2 \pmod{43}, \nonumber\] which is equivalent to, since \(44\equiv1\) (mod 43), \[x_1 \equiv x_2 \pmod{43}. \nonumber\] Therefore, \(x_1=x_2\) in \(\mathbb{Z}_{43}\). This proves that \(g\) is one-to-one.
exercise \(\PageIndex{6}\label{he:oneonefcn-06}\)
Is the function \( h : {\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}\) defined by \[h(x) \equiv 4x-11 \pmod{15} \nonumber\] a one-to-one function?
exercise \(\PageIndex{7}\label{he:oneonefcn-07}\)
Show that the function \(k:{\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}\) defined by \[k(x) \equiv 5x-11 \pmod{15} \nonumber\] is not one-to-one by finding \(x_1\neq x_2\) such that \(k(x_1)=k(x_2)\).
Example \(\PageIndex{8}\label{eg:oneonefcn-08}\)
In the last exercise, we should not rely on the non-existence of \(5^{-1}\) in \(\mathbb{Z}_{15}\) to prove that \(k\) is not one-to-one. One must consider the interaction between the domain, the codomain, and the definition of the function. For example, despite the fact that \(5^{-1}\) does not exist in \(\mathbb{Z}_{15}\), the function \(p :{\mathbb{Z}_3}\to{\mathbb{Z}_{15}}\) defined by \[p(x) \equiv 5x-11 \pmod{15} \nonumber\] is one-to-one, because \(p(0)=4\), \(p(1)=9\), and \(p(2)=14\) are distinct images.
The last example illustrates the trickiness in a function with different moduli in its domain and codomain. Use caution when you deal with such functions! Sometimes, infinite sets also pose a challenge. Because there is an infinite supply of elements, we may obtain results that appear to be impossible for finite sets.
Example \(\PageIndex{9}\label{eg:oneonefcn-09}\)
The function \( f : {\mathbb{Z}}\to{\mathbb{Z}}\) defined by \[f(n) = \cases{ \frac{n}{2} & if $n$ is even \cr \frac{n+1}{2} & if $n$ is odd \cr} \nonumber\] is not one-to-one, because, for example, \(f(0)=f(-1)=0\). The function \( g : {\mathbb{Z}}\to{\mathbb{Z}}\) defined by \[g(n) = 2n \nonumber\] is one-to-one, because if \(g(n_1)=g(n_2)\), then \(2n_1=2n_2\) implies that \(n_1=n_2\).
exercise \(\PageIndex{8}\label{he:oneonefcn-08}\)
Show that the function \( h : {\mathbb{Z}}\to{\mathbb{N}}\) defined by \[h(n) = \cases{ 2n+1 & if $n\geq0$, \cr -2n & if $n < 0$, \cr} \nonumber\] is one-to-one.
Example \(\PageIndex{10}\label{eg:oneonefcn-10}\)
Let \(A\) be the set of all married individuals from a monogamous community who are neither divorced nor widowed. Then the function \(s:{A}\to{A}\) defined by \[s(x) = \mbox{ spouse of } x \nonumber\] is one-to-one. The reason is, it is impossible to have \(x_1\neq x_2\) and yet \(s(x_1)=s(x_2)\).
Summary and Review
- A function \(f\) is said to be one-to-one if \(f(x_1) = f(x_2) \Rightarrow x_1=x_2\).
- No two images of a one-to-one function are the same.
- To show that a function \(f\) is not one-to-one, all we need is to find two different \(x\)-values that produce the same image; that is, find \(x_1\neq x_2\) such that \(f(x_1)=f(x_2)\).
Exercise \(\PageIndex{1}\label{ex:oneonefcn-01}\)
Which of the following functions are one-to-one? Explain.
- \( f : {\mathbb{R}}\to{\mathbb{R}}\), \(f(x)=x^3-2x^2+1\).
- \( g : {[\,2,\infty)}\to{\mathbb{R}}\), \(f(x)=x^3-2x^2+1\).
Exercise \(\PageIndex{2}\label{ex:oneonefcn-02}\)
Which of the following functions are one-to-one? Explain.
- \(p :{\mathbb{R}}\to{\mathbb{R}}\), \(h(x)=e^{1-2x}\).
- \( q :{\mathbb{R}}\to{\mathbb{R}}\), \(p(x)=|1-3x|\).
Exercise \(\PageIndex{3}\label{ex:oneonefcn-03}\)
Construct a one-to-one function \( f : {(1,3)}\to{(2,5)}\) so that \( f : {[\,1,3)}\to{[\,2,5)}\) is still one-to-one.
Exercise \(\PageIndex{4}\label{ex:oneonefcn-04}\)
Construct a one-to-one function \( g : {[\,2,5)}\to{(1,4\,]}\).
Exercise \(\PageIndex{5}\label{ex:oneonefcn-05}\)
Determine which of the following are one-to-one functions.
- \( f : {\mathbb{Z}}\to{\mathbb{Z}}\); \(f(n)=n^3+1\)
- \( g : {\mathbb{Q}}\to{\mathbb{Q}}\); \(g(x)=n^2\)
- \( h : {\mathbb{R}}\to{\mathbb{R}}\); \(h(x)=x^3-x\)
- \({k} : {\mathbb{R}}\to{\mathbb{R}}\); \(k(x)=5^x\)
Exercise \(\PageIndex{6}\label{ex:oneonefcn-06}\)
Determine which of the following are one-to-one functions.
- \(p :{\wp(\{1,2,3,\ldots,n\})}\to{\{0,1,2,\ldots,n\}}\); \(p(S)=|S|\)
- \( q :{\wp(\{1,2,3,\ldots,n\})}\to{\wp(\{1,2,3,\ldots,n\})}\); \(q(S)=\overline{S}\)
Exercise \(\PageIndex{7}\label{ex:oneonefcn-07}\)
Determine which of the following functions are one-to-one.
- \({f_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d\}}\); \(f_1(1)=b\), \(f_1(2)=c\), \(f_1(3)=a\), \(f_1(4)=a\), \(f_1(5)=c\)
- \({f_2}:{\{1,2,3,4\}}\to{\{a,b,c,d,e\}}\); \(f_2(1)=c\), \(f_2(2)=b\), \(f_2(3)=a\), \(f_2(4)=d\)
- \({f_3}:{\mathbb{Z}}\to{\mathbb{Z}}\); \(f_5(n)=-n\)
- \(f_4: \mathbb{Z} \rightarrow \mathbb{Z}\); \(f_4(n) = \cases{ 2n & if $n < 0$, \cr -3n & if $n\geq0$,\cr}\)
Exercise \(\PageIndex{8}\label{ex:oneonefcn-08}\)
Determine which of the following functions are one-to-one.
- \({g_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_1(1)=b\), \(g_1(2)=b\), \(g_1(3)=b\), \(g_1(4)=a\), \(g_1(5)=d\)
- \({g_2}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_2(1)=d\), \(g_2(2)=b\), \(g_2(3)=e\), \(g_2(4)=a\), \(g_2(5)=c\)
- \(g_3: \mathbb{N} \rightarrow \mathbb{N}\); \(g_3 (n) = \cases{ \frac{n+1}{2} & if $n$ is odd \cr \frac{n}{2} & if $n$ is even \cr}\)
- \(g_4: \mathbb{N} \rightarrow \mathbb{N}\); \(g_4 (n) = \cases{ n+1 & if $n$ is odd \cr n-1 & if $n$ is even \cr}\)
Exercise \(\PageIndex{9}\label{ex:oneonefcn-09}\)
List all the one-to-one functions from \(\{1,2\}\) to \(\{a,b,c,d\}\).
- Hint
-
List the images of each function.
Exercise \(\PageIndex{10}\label{ex:oneonefcn-10}\)
Is it possible to find a one-to-one function from \(\{1,2,3,4\}\) to \(\{1,2\}\)? Explain.
Exercise \(\PageIndex{11}\label{ex:oneonefcn-11}\)
Determine which of the following functions are one-to-one.
- \( f : {\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(h(n)\equiv 3n\) (mod 10).
- \( g : {\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(g(n)\equiv 5n\) (mod 10).
- \( h : {\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(h(n)\equiv 3n\) (mod 36).
Exercise \(\PageIndex{12}\label{ex:oneonefcn-12}\)
Determine which of the following functions are one-to-one.
- \(r:{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(r(n)\equiv 5n\) (mod 36).
- \(s:{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(s(n)\equiv n+5\) (mod 10).
- \(t:{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(t(n)\equiv 3n+5\) (mod 10).
Exercise \(\PageIndex{13}\label{ex:oneonefcn-13}\)
Determine which of the following functions are one-to-one.
- \(\alpha:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{ 7}}\); \(\alpha(n)\equiv 2n\) (mod 7).
- \(\beta :{\mathbb{Z}_{ 8}}\to{\mathbb{Z}_{12}}\); \(\beta (n)\equiv 3n\) (mod 12).
- \(\gamma:{\mathbb{Z}_{ 6}}\to{\mathbb{Z}_{12}}\); \(\gamma(n)\equiv 2n\) (mod 12).
- \(\delta:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{36}}\); \(\delta(n)\equiv 6n\) (mod 36).
Exercise \(\PageIndex{14}\label{ex:oneonefcn-14}\)
Give an example of a one-to-one function \(f\) from \(\mathbb{N}\) to \(\mathbb{N}\) that is not the identity function.


