6.7: Composite Functions
- Page ID
- 8562
Given functions \(f :{A}\to{B}\) and \(g :{B}\to{C}\), the composite function, \(g\circ f\), which is pronounced as “\(g\) circle \(f\)”, is defined as \[{g\circ f}:{A}\to{C}, \qquad (g\circ f)(x) = g(f(x)). \nonumber\] The image is obtained in two steps. First, \(f(x)\) is obtained. Next, it is passed to \(g\) to obtain the final result. It works like connecting two machines to form a bigger one, see Figure \(\PageIndex{1}\). We can also use an arrow diagram to provide another pictorial view, see Figure \(\PageIndex{2}\).
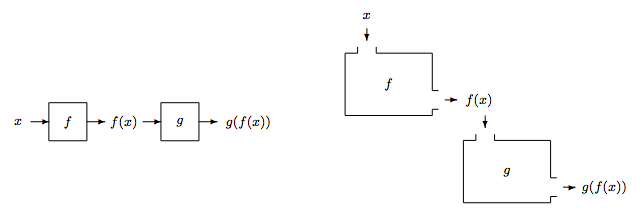
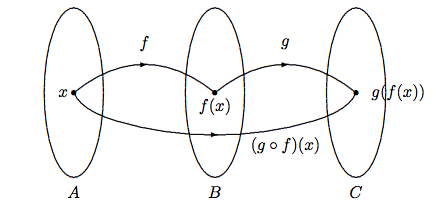
Numeric value of \((g\circ f)(x)\) can be computed in two steps. For example, to compute \((g\circ f)(5)\), we first compute the value of \(f(5)\), and then the value of \(g(f(5))\). To find the algebraic description of \((g\circ f)(x)\), we need to compute and simplify the formula for \(g(f(x))\). In this case, it is often easier to start from the “outside” function. More precisely, start with \(g\), and write the intermediate answer in terms of \(f(x)\), then substitute in the definition of \(f(x)\) and simplify the result.
Example \(\PageIndex{1}\label{eg:compfcn-01}\)
Assume \(f,g :{\mathbb{R}}\to{\mathbb{R}}\) are defined as \(f(x)=x^2\), and \(g(x)=3x+1\). We find
\[\displaylines{ (g\circ f)(x)=g(f(x))=3[f(x)]+1=3x^2+1, \cr (f\circ g)(x)=f(g(x))=[g(x)]^2=(3x+1)^2. \cr} \nonumber\]
Therefore,
\[g \circ f: \mathbb{R} \to \mathbb{R}, \qquad (g \circ f)(x)=3x^2+1 \nonumber\]
\[f \circ g: \mathbb{R} \to \mathbb{R}, \qquad (f \circ g)(x)=(3x+1)^2 \nonumber\]
We note that, in general, \(f\circ g \neq g\circ f\).
hands-on exercise \(\PageIndex{1}\label{he:compfcn-01}\)
If \(p,q:\mathbb{R} \to \mathbb{R}\) are defined as \(p(x)=2x+5\), and \(q(x)=x^2+1\), determine \(p\circ q\) and \(q\circ p\). Do not forget to describe the domain and the codomain.
hands-on exercise \(\PageIndex{2}\label{he:compfcn-02}\)
The functions \(f,g :\mathbb{Z}_{12} \to \mathbb{Z}_{12}\) are defined by
\[f(x) \equiv 7x+2 \pmod{12}, \qquad\mbox{and}\qquad g(x) \equiv 5x-3 \pmod{12}. \nonumber\]
Compute the composite function \(f\circ g\).
Example \(\PageIndex{2}\label{eg:compfcn-02}\)
Define \(f,g :{\mathbb{R}}\to{\mathbb{R}}\) as
\[f(x) = \cases{ 3x+1 & if $x < 0$, \cr 2x+5 & if $x\geq0$, \cr} \nonumber\]
and \(g(x)=5x-7\). Find \(g\circ f\).
- Answer
-
Since \(f\) is a piecewise-defined function, we expect the composite function \(g\circ f\) is also a piecewise-defined function. It is defined by \[(g\circ f)(x) = g(f(x)) = 5f(x)-7 = \cases{ 5(3x+1)-7 & if $x < 0$, \cr 5(2x+5)-7 & if $x\geq0$. \cr} \nonumber\]
After simplification, we find \(g \circ f: \mathbb{R} \to \mathbb{R}\), by: \[(g\circ f)(x) = \cases{ 15x-2 & if $x < 0$, \cr 10x+18 & if $x\geq0$. \cr} \nonumber\] In this example, it is rather obvious what the domain and codomain are. Nevertheless, it is always a good practice to include them when we describe a function.
hands-on exercise \(\PageIndex{3}\label{he:compfcn-03}\)
The functions \(f :{\mathbb{R}}\to{\mathbb{R}}\) and \(g :{\mathbb{R}}\to{\mathbb{R}}\) are defined by \[f(x) = 3x+2, \qquad\mbox{and}\qquad g(x) = \cases{ x^2 & if $x\leq5$, \cr 2x-1 & if $x > 5$. \cr} \nonumber\] Determine \(f\circ g\).
The next example further illustrates why it is often easier to start with the outside function \(g\) in the derivation of the formula for \(g(f(x))\).
Example \(\PageIndex{3}\label{eg:compfcn-03}\)
The function \(p :{[1,5]}\to{\mathbb{R}}\) is defined by
\[p(x) = \cases{ 2x+3 & if $1\leq x< 3$, \cr 5x-2 & if $3\leq x\leq 5$; \cr} \nonumber\]
and the function \(q :{\mathbb{R}}\to{\mathbb{R}}\) by
\[q(x) = \cases{ 4x & if $x < 7$, \cr 3x & if $x\geq7$. \cr} \nonumber\]
Describe the function \(q\circ p\).
- Answer
-
Since \[(q\circ p)(x) = q(p(x)) = \cases{ 4p(x) & if $p(x)<7$, \cr 3p(x) & if $p(x)\geq7$, \cr} \nonumber\] we have to find out when will \(p(x)<7\), and when will \(p(x)\geq7\), because these conditions determine what we need to do next to continue the computation. Since \(p(x)\) is computed in two different ways, we have to analyze two cases.
Case 1: \(1\leq x<3\). In this case, \(p(x)\) is defined as \(2x+3\). This is an increasing function, hence, \[p(x)\geq p(1) = 2\cdot1+3 = 5, \qquad\mbox{and}\qquad p(x) < p(3) = 2\cdot3+3 = 9. \nonumber\] For some \(x\)s in this range, we have \(p(x)<7\), but for other \(x\)-values, we have \(p(x)\geq7\). We need to know the cut-off point. This happens when \(p(x)=2x+3=7\), that is, when \(x=2\). This leads to two subcases.
- Case 1a: When \(1\leq x<2\), we have \(p(x)=2x+3 <7\). Thus, \[q(p(x)) = 4p(x) = 4(2x+3) = 8x+12. \nonumber\]
- Case 1b: When \(2\leq x<3\), we have \(p(x)=2x+3\geq7\). Thus, \[q(p(x)) = 3p(x) = 3(2x+3) = 6x+9. \nonumber\]
Case 2: \(3\leq x\leq 5\). In this case, \(p(x)\) is computed as \(5x-2\). This is an increasing function, hence \(p(x) \geq p(3) = 5\cdot3-2=13\). Since \(p(x)\) is always greater than 7, we find \[q(p(x)) = 3p(x) = 3(5x-2) = 15x-6. \nonumber\]
Combining these cases, we determine that the composite function \({q\circ p\,}{[1,5]}\to{\mathbb{R}}\) is defined by \[(q\circ p)(x) = \cases{ 8x+12 & if $1\leq x<2$, \cr 6x+9 & if $2\leq x<3$, \cr 15x-6 & if $3\leq x\leq5$. \cr} \nonumber\] Study this example again to make sure that you understand it thoroughly.
hands-on exercise \(\PageIndex{4}\label{he:compfcn-04}\)
The functions \(f,g :{\mathbb{Z}}\to{\mathbb{Z}}\) are defined by \[f(n) = \cases{ n+1 & if $n$ is even \cr n-1 & if $n$ is odd \cr} \qquad g(n) = \cases{ n+3 & if $n$ is even \cr n-7 & if $n$ is odd \cr} \nonumber\] Determine \(f\circ g\).
Strictly speaking, \(g\circ f\) is well-defined if the codomain of \(f\) equals to the domain of \(g\). It is clear that \(g\circ f\) is still well-defined if \(\mathrm{ im }{f}\) is a subset of the domain of \(g\). Hence, if \[f :{A}{B}, \quad g :{C}{D}, \nonumber\] then \(g\circ f\) is well-defined if \(B\subseteq C\), or more generally, \(\mathrm{ im }{f}\subseteq C\).
Example \(\PageIndex{4}\label{eg:compfcn-04}\)
Let \(\mathbb{R}^*\) denote the set of nonzero real numbers. Suppose
\[f : \mathbb{R}^* \to \mathbb{R}, \qquad f(x)=\frac{1}{x} \nonumber\]
\[g : \mathbb{R} \to (0, \infty), \qquad g(x)=3x^2+11. \nonumber\]
Determine \(f\circ g\) and \(g\circ f\). Be sure to specify their domains and codomains.
- Answer
-
To compute \(f\circ g\), we start with \(g\), whose domain is \(\mathbb{R}\). Hence, \(\mathbb{R}\) is the domain of \(f\circ g\). The result from \(g\) is a number in \((0,\infty)\). The interval \((0,\infty)\) contains positive numbers only, so it is a subset of \(\mathbb{R}^*\). Therefore, we can continue our computation with \(f\), and the final result is a number in \(\mathbb{R}\). Hence, the codomain of \(f\circ g\) is \(\mathbb{R}\). The image is computed according to \(f(g(x)) = 1/g(x) = 1/(3x^2+11)\). We are now ready to present our answer:
\(f \circ g: \mathbb{R} \to \mathbb{R},\) by:
\[(f \circ g)(x) = \frac{1}{3x^2+11}. \nonumber\]
In a similar manner, the composite function \(g\circ f :{\mathbb{R}^*} {(0,\infty)}\) is defined as \[(g\circ f)(x) = \frac{3}{x^2}+11. \nonumber\] Be sure you understand how we determine the domain and codomain of \(g\circ f\).
hands-on exercise \(\PageIndex{5}\label{he:compfcn-05}\)
Let \(\mathbb{Z}\) denote the set of integers. Determine \(h\circ g\), where \[\begin{array}{cc} g: \mathbb{Z} \to \mathbb{R}, & g(x) = \sqrt{|x|}, \\ h: \mathbb{R} \to \mathbb{R}, & h(x) = (x-5)^2 \end{array} \nonumber\] Is \(g\circ h\) well-defined? Explain!
As usual, take extra caution with modular arithmetic.
Example \(\PageIndex{5}\label{eg:compfcn-05}\)
Define \(f :{\mathbb{Z}_{15}}\to{\mathbb{Z}_{23}}\) and \(g :{\mathbb{Z}_{23}}\to{\mathbb{Z}_{32}}\) according to
\[\begin{aligned} f(x) &\equiv& 3x+5 \pmod{23}, \\ g(x) &\equiv& 2x+1 \pmod{32}. \end{aligned} \nonumber\]
We may expect \(g\circ f :{\mathbb{Z}_{15}}\to{\mathbb{Z}_{23}}\) to be defined as
\[(g\circ f)(x) \equiv 2(3x+5)+1 \equiv 6x+11) \pmod{32}. \nonumber\]
In particular, \((g\circ f)(8) \equiv 59 \equiv 27\) (mod 32).
If we perform the computation one step at a time, we find \(f(8)\equiv 29\equiv6\) (mod 23), from which we obtain \[(g\circ f)(8) = g(f(8)) = g(6) \equiv 13 \pmod{32}. \nonumber\] which is not what we have just found. Can you explain why?
- Answer
-
The source of the problem is the different moduli used in \(f\) and \(g\). The composite function should be defined as \[(g\circ f)(x) \equiv 2r+1 \pmod{32}, \qquad\mbox{where } r \equiv 3x+5 \pmod{23}. \nonumber\] In a way, this definition forces us to carry out the computation in two steps. Consequently, we will obtain the correct answer \((g\circ f)(8)=13\).
There is a close connection between a bijection and its inverse function, from the perspective of composition.
Theorem \(\PageIndex{1}\label{thm:compfcn-inv}\)
For a bijective function \(f :{A}\to{B}\),
\[f^{-1}\circ f=i_A, \qquad\mbox{and}\qquad f\circ f^{-1}=i_B, \nonumber\]
where \(i_A\) and \(i_B\) denote the identity function on \(A\) and \(B\), respectively.
- Proof
-
To prove that \(f^{-1}\circ f = i_A\), we need to show that \((f^{-1}\circ f)(a)=a\) for all \(a\in A\). Assume \(f(a)=b\). Then, because \(f^{-1}\) is the inverse function of \(f\), we know that \(f^{-1}(b)=a\). Therefore,
\[(f^{-1}\circ f)(a) = f^{-1}(f(a)) = f^{-1}(b) = a, \nonumber\]
which is what we want to show. The proof of \(f\circ f^{-1} = i_B\) procceds in the exact same manner, and is omitted here.
Example \(\PageIndex{6}\label{eg:compfcn-06}\)
Show that the functions \(f,g :{\mathbb{R}}\to{\mathbb{R}}\) defined by \(f(x)=2x+1\) and \(g(x)=\frac{1}{2}(x-1)\) are inverse functions of each other.
- Answer
-
The problem does not ask you to find the inverse function of \(f\) or the inverse function of \(g\). Instead, the answers are given to you already. You job is to verify that the answers are indeed correct, that the functions are inverse functions of each other.
Form the two composite functions \(f\circ g\) and \(g\circ f\), and check whether they both equal to the identity function:
\[\displaylines{ \textstyle (f\circ g)(x) = f(g(x)) = 2 g(x)+1 = 2\left[\frac{1}{2}(x-1)\right]+1 = x, \cr \textstyle (g\circ f)(x) = g(f(x)) = \frac{1}{2} \big[f(x)-1\big] = \frac{1}{2} \left[(2x+1)-1\right] = x. \cr} \nonumber\]
We conclude that \(f\) and \(g\) are inverse functions of each other.
hands-on exercise \(\PageIndex{6}\label{he:compfcn-06}\)
Verify that \(f :{\mathbb{R}}\to{\mathbb{R}^+}\) defined by \(f(x)=e^x\), and \(g :{\mathbb{R}^+}\to{\mathbb{R}}\) defined by \(g(x)=\ln x\), are inverse functions of each other.
Theorem \(\PageIndex{2}\label{thm:compfcn-02}\)
Suppose \(f :{A}\to{B}\) and \(g :{B}\to{C}\). Let \(i_A\) and \(i_B\) denote the identity function on \(A\) and \(B\), respectively. We have the following results.
- \(f\circ i_A=f\) and \(i_B\circ f=f\).
- If both \(f\) and \(g\) are one-to-one, then \(g\circ f\) is also one-to-one.
- If both \(f\) and \(g\) are onto, then \(g\circ f\) is also onto.
- If both \(f\) and \(g\) are bijective, then \(g\circ f\) is also bijective. In fact, \((g\circ f)^{-1}= f^{-1}\circ g^{-1}\).
- Proof of (a)
-
To show that \(f\circ i_A=f\), we need to show that \((f\circ i_A)(a)= f(a)\) for all \(a\in A\). This follows from direct computation: \[(f\circ i_A)(a) = f(i_A(a)) = f(a). \nonumber\] The proofs of \(i_B\circ f=f\) and (b)–(d) are left as exercises.
Example \(\PageIndex{7}\label{eg:compfcn-07}\)
The converses of (b) and (c) in Theorem 6.7.2 are false, as demonstrated in the functions
\[\begin{array}{cc} g: \mathbb{Z} \to \mathbb{Z}, & f(x)=2x, \\ h: \mathbb{Z} \to \mathbb{Z}, & g(x)= \lfloor x/2 \rfloor \end{array} \nonumber\]
Here, \(g\circ f=i_{\mathbb{Z}}\), so \(g\circ f\) is one-to-one, and it is obvious that \(f\) is also one-to-one, but \(g\) is not one-to-one. It is easy to see that both \(g\) and \(g\circ f\) are onto, but \(f\) is not.
Summary and Review
- The composition of two functions \(f :{A}\to{B}\) and \(g :{B}\to{C}\) is the function \(g\circ f :{A}\to{C}\) defined by \((g\circ f)(x)=g(f(x))\).
- If \(f :{A}\to{B}\) is bijective, then \(f^{-1}\circ f=i_A\) and \(f\circ f^{-1}=i_B\).
- To check whether \(f :{A}\to{B}\) and \(g :{B}\to{A}\) are inverse of each other, we need to show that
- \((g\circ f)(x)=g(f(x))=x\) for all \(x\in A\), and
- \((f\circ g)(y)=f(g(y))=y\) for all \(y\in B\).
exercise \(\PageIndex{1}\label{ex:compfcn-01}\)
The functions \(g,f:{\mathbb{R}}\to{\mathbb{R}}\) are defined by \(f(x)=5x-1\) and \(g(x)=3x^2+4\). Determine \(f\circ g\) and \(g\circ f\).
exercise \(\PageIndex{2}\label{ex:compfcn-02}\)
The function \(h :{(0,\infty)}\to{(0,\infty)}\) is defined by \(h(x)=x+\frac{1}{x}\). Determine \(h\circ h\). Simplify your answer as much as possible.
exercise \(\PageIndex{3}\label{ex:compfcn-03}\)
The functions \(g,f :{\mathbb{R}}\to{\mathbb{R}}\) are defined by \(f(x)=1-3x\) and \(g(x)=x^2+1\). Evaluate \(f(g(f(0)))\).
exercise \(\PageIndex{4}\label{ex:compfcn-04}\)
The functions \(p :{(2,8]}\to{\mathbb{R}}\) and \(q :{\mathbb{R}}\to{\mathbb{R}}\) are defined by \[\begin{array}{rcl} p(x) &=& \cases{ 3x-1 & if $2<x\leq 4$, \cr 17-2x & if $4<x\leq 8$, \cr} \\ q(x) &=& \cases{ 4x-1 & if $x < 3$, \cr 3x+1 & if $x\geq3$. \cr} \end{array} \nonumber\] Evaluate \(q\circ p\).
exercise \(\PageIndex{5}\label{ex:compfcn-05}\)
Describe \(g\circ f\).
- \(f :{\mathbb{Z}}\to{\mathbb{N}}\), \(f(n)=n^2+1\); \(g :{\mathbb{N}}\to{\mathbb{Q}}\), \(g(n)=\frac{1}{n}\).
- \(f :{\mathbb{R}}\to{(0,1)}\), \(f(x)=1/(x^2+1)\); \(g :{(0,1)}\to{(0,1)}\), \(g(x)=1-x\).
- \(f :{\mathbb{Q}-\{2\}}\to{\mathbb{Q}^*}\), \(f(x)=1/(x-2)\); \(g :{\mathbb{Q}^*}\to{\mathbb{Q}^*}\), \(g(x)=1/x\).
- \(f :{\mathbb{R}}\to{[\,1,\infty)}\),\(f(x)=x^2+1\); \(g :{[\,1,\infty)}\to {[\,0,\infty)}\) \(g(x)=\sqrt{x-1}\).
- \(f :{\mathbb{Q}-\{10/3\}}\to{\mathbb{Q}-\{3\}}\),\(f(x)=3x-7\); \(g :{\mathbb{Q}-\{3\}}\to{\mathbb{Q}-\{2\}}\), \(g(x)=2x/(x-3)\).
exercise \(\PageIndex{6}\label{ex:compfcn-06}\)
Describe \(g\circ f\).
- \(f :{\mathbb{Z}}\to{\mathbb{Z}_5}\), \(f(n)\equiv n\) (mod 5); \(g :{\mathbb{Z}_5}\to{\mathbb{Z}_5}\), \(g(n)\equiv n+1\) (mod 5).
- \(f :{\mathbb{Z}_8}\to{\mathbb{Z}_{12}}\), \(f(n)\equiv 3n\) (mod 12); \(g :\to{\mathbb{Z}_{12}}{\mathbb{Z}_6}\), \(g(n)\equiv 2n\) (mod 6).
exercise \(\PageIndex{7}\label{ex:compfcn-07}\)
Describe \(g\circ f\).
- \(f :{\{1,2,3,4,5\}}\to{\{1,2,3,4,5\}}\), \(f(1)=5\), \(f(2)=3\), \(f(3)=2\), \(f(4)=1\), \(f(5)=4\);
- \(g :{\{1,2,3,4,5\}}\to{\{1,2,3,4,5\}}\); \(g(1)=3\), \(g(2)=1\), \(g(3)=5\), \(g(4)=4\), \(g(5)=2\)
- \(f :{\{a,b,c,d,e\}}\to{\{1,2,3,4,5\}}\); \(f(a)=5\), \(f(b)=1\), \(f(c)=2\), \(f(d)=4\), \(f(e)=3\);
- \(g :{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g(1)=e\), \(g(2)=d\), \(g(3)=a\), \(g(4)=c\), \(g(5)=b\)
exercise \(\PageIndex{8}\label{ex:compfcn-08}\)
Verify that \(f,g:{\mathbb{R}}\to{\mathbb{R}}\) defined by \[f(x) = \cases{ 11-2x & if $x<4$ \cr 15-3x & if $x\geq4$ \cr} \qquad\mbox{and}\qquad g(x) = \cases{ \textstyle \frac{1}{3}(15-x) & if $x\leq3$ \cr \textstyle \frac{1}{2}(11-x) & if $x > 3$ \cr} \nonumber\] are inverse to each other.
exercise \(\PageIndex{9}\label{ex:compfcn-09}\)
The functions \(f,g :{\mathbb{Z}}\to{\mathbb{Z}}\) are defined by \[f(n) = \cases{ 2n-1 & if $n\geq0$ \cr 2n & if $n < 0$ \cr} \qquad\mbox{and}\qquad g(n) = \cases{ n+1 & if $n$ is even \cr 3n & if $n$ is odd \cr} \nonumber\] Determine \(g\circ f\).
exercise \(\PageIndex{10}\label{ex:compfcn-10}\)
Define the functions \(f\) and \(g\) on your maternal family tree (see Problem 6.7.8 in Exercises 1.2) according to \[\begin{array}{rcl} f(x) &=& \mbox{the mother of $x$}, \\ g(x) &=& \mbox{the eldest daughter of the mother of $x$}. \end{array} \nonumber\] Describe these functions.
- \(f\circ g\)
- \(g\circ f\)
- \(f\circ f\)
- \(g\circ g\)
exercise \(\PageIndex{11}\label{ex:compfcn-11}\)
Given the bijections \(f\) and \(g\), find \(f\circ g\), \((f\circ g)^{-1}\) and \(g^{-1}\circ f^{-1}\).
- \(f :{\mathbb{Z}}\to{\mathbb{Z}}\), \(f(n)=n+1\); \(g :{\mathbb{Z}}\to{\mathbb{Z}}\), \(g(n)=2-n\).
- \(f :{\mathbb{Q}}\to{\mathbb{Q}}\), \(f(x)=5x\); \(g :{\mathbb{Q}}\to{\mathbb{Q}}\), \(g(x)=\frac{x-2}{5}\).
- \(f :{\mathbb{Q}-\{2\}}\to{\mathbb{Q}-\{2\}}\), \(f(x)=3x-4\); \(g :{\mathbb{Q}-\{2\}}\to{\mathbb{Q}-\{2\}}\), \(g(x)=\frac{x}{x-2}\).
- \(f :{\mathbb{Z}_7}\to{\mathbb{Z}_7}\), \(f(n)\equiv 2n+5\) (mod 7); \(g :{\mathbb{Z}_7}\to{\mathbb{Z}_7}\), \(g(n)\equiv 3n-2\) (mod 7).
exercise \(\PageIndex{12}\label{ex:compfcn-12}\)
Give an example of sets \(A\), \(B\), and \(C\), and of functions \(f :{A}\to{B}\) and \(g :{B}\to{C}\), such that \(g\circ f\) and \(f\) are both one-to-one, but \(g\) is not one-to-one.
exercise \(\PageIndex{13}\label{ex:compfcn-13}\)
Prove part (b) of Theorem 6.7.2.
exercise \(\PageIndex{14}\label{ex:compfcn-14}\)
Prove part (c) of Theorem 6.7.2.
exercise \(\PageIndex{15}\label{ex:compfcn-15}\)
Prove part (d) of Theorem 6.7.2.
exercise \(\PageIndex{16}\label{ex:compfcn-16}\)
The incidence matrices for the functions \(f :{\{a,b,c,d,e\}} \to{\{x,y,z,w\}}\) and \(g :{\{x,y,z,w\}}\to{\{1,2,3,4,5,6\}}\) are \[\begin{array}{ccccc} & \begin{array}{cccc} x & y & z & w \end{array} & & & \begin{array}{cccccc} 1 & 2 & 3 & 4 & 5 & 6 \end{array} \\ \begin{array}{c} a \\ b \\ c \\ d \\ e \end{array} & \left( \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array} \right) & \text{ and } & \begin{array}{c} x \\ y \\ z \\ w \end{array} & \left( \begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{array} \right) \end{array} \nonumber\] respectively. Construct the incidence matrix for the composition \(g\circ f\).


