6.3: Pólya-Redfield Enumeration Theory
- Page ID
- 6122
George Pólya and Robert Redfield independently developed a theory of generating functions that describe the action of a group \(G\) on colorings of a set \(S\) by a set \(T\) when we know the action of \(G\) on \(S\). Pólya’s work on the subject is very accessible in its exposition, and so the subject has become popularly known as Pólya theory, though Pólya-Redfield theory would be a better name. In this section, we develop the elements of this theory.
The idea of coloring a set \(S\) has many applications. For example, the set \(S\) might be the positions in a hydrocarbon molecule which are occupied by hydrogen, and the group could be the group of spatial symmetries of the molecule (that is, the group of permutations of the atoms of the molecule that move the molecule around so that in its final position the molecule cannot be distinguished from the original molecule). The colors could then be radicals (including hydrogen itself) that we could substitute for each hydrogen position in the molecule. Then the number of orbits of colorings is the number of chemically different compounds we could create by using these substitutions.1
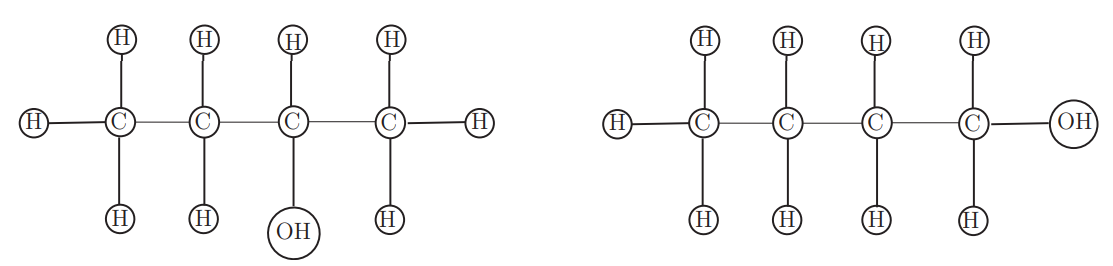
In Figure 6.3.1 we show two different ways to substitute the \(\text{OH}\) radical for a hydrogen atom in the chemical diagram we gave for butane in Chapter 2. We have colored one vertex of degree \(1\) with the radical \(\text{OH}\) and the rest with the atom \(\text{H}\). There are only two distinct ways to do this, as the \(\text{OH}\) must either connect to an “end” \(\text{C}\) or a “middle” \(\text{C}\). This shows that there are two different forms, called isomers of the compound shown. This compound is known as butyl alcohol.
So think intuitively about some “figure” that has places to be colored. (Think of the faces of a cube, the beads on a necklace, circles at the vertices of an \(n\)-gon, etc.) How can we picture the coloring? If we number the places to be colored, say \(1\) to \(n\), then we have a standard way to represent our coloring. For example, if our colors are blue, green and red, then \(BBGRRGBG\) describes a typical coloring of \(8\) such places. Unless the places are somehow “naturally” numbered, this idea of a coloring imposes structure that is not really there. Even if the structure is there, visualizing our colorings in this way doesn’t “pull together” any common features of different colorings; we are simply visualizing all possible colorings. We have a group (think of it as symmetries of the figure you are imagining) that acts on the places. That group then acts in a natural way on the colorings of the places and we are interested in orbits of the colorings. Thus we want a picture that pulls together the common features of the colorings in an orbit. One way to pull together similarities of colorings would be to let the letters we are using as pictures of colors commute as we did with our pictures in Chapter 4; then our picture \(BBGRRGBG\) becomes \(B^3G^3R^2\), so our picture now records simply how many times we use each color. Think about how we defined the action of a group on the colorings of a set on which the group acts. You will see that acting with a group element won’t change how many times each color is used; it simply moves colors to different places. Thus the picture we now have of a given coloring is an equally appropriate picture for each coloring in an orbit. One natural question for us to ask is “How many orbits have a given picture?”
Exercise \(310\)
Suppose we draw identical circles at the vertices of a regular hexagon. Suppose we color these circles with two colors, red and blue.
- In how many ways may we color the set \(\{1, 2, 3, 4, 5, 6\}\) using the colors red and blue?
- These colorings are partitioned into orbits by the action of the rotation group on the hexagon. Using our standard notation, write down all these orbits and observe how many orbits have each picture, assuming the picture of a coloring is the product of commuting variables representing the colors.
- Using the picture function of the previous part, write down the picture enumerator for the orbits of colorings of the vertices of a hexagon under the action of the rotation group.
In Problem 310c, we saw a picture enumerator for pictures of orbits of the action of a group on colorings. As above, we ask how many orbits of the colorings have any given picture. We can think of a multivariable generating function in which the letters we use to picture individual colors are the variables, and the coefficient of a picture is the number of orbits with that picture. Such a generating function provides an answer to our natural question, and so it is this sort of generating function we will seek. Since the CFB theorem was our primary tool for saying how many orbits we have, it makes sense to think about whether the CFB theorem has an analog in terms of pictures of orbits.
6.3.1: The Orbit-Fixed Point Theorem
\(\bullet\) Exercise \(311\)
Suppose now we have a group \(G\) acting on a set and we have a picture function on that set with the additional feature that for each orbit of the group, all its elements have the same picture. In this circumstance, we define the picture of an orbit or multiorbit to be the picture of any one of its members. The orbit enumerator \(\text{Orb}(G, S)\) is the sum of the pictures of the orbits. (Note that this is the same as the sum of the pictures of the multiorbits.) The fixed point enumerator \(\text{Fix}(G, S)\) is the sum of the pictures of each of the fixed points of each of the elements of \(G\). We are going to construct a generating function analog of the CFB theorem. The main idea of the proof of the CFB theorem was to try to compute in two different ways the number of elements (i.e. the sum of all the multiplicities of the elements) in the union of all the multiorbits of a group acting on a set. Suppose instead we try to compute the sum of all the pictures of all the elements in the union of the multiorbits of a group acting on a set. By thinking about how this sum relates to \(\text{Orb}(G, S)\) and \(\text{Fix}(G, S)\), find an analog of the CFB theorem that relates these two enumerators. State and prove this theorem.
We will call the theorem of Problem 311 the Orbit-Fixed Point Theorem. In order to apply the Orbit-Fixed Point Theorem, we need some basic facts about picture enumerators.
\(\bullet\) Exercise \(312\)
Suppose that \(P_1\) and \(P_2\) are picture functions on sets \(S_1\) and \(S_2\) in the sense of Section 4.1.2. Define \(P\) on \(S_1 \times S_2\) by \(P(x_1, x_2) = P_1(x_1)P_2(x_2)\). How are \(E_{P_1}\), \(E_{P_1}\), and \(E_P\) related? (You may have already done this problem in another context!)
\(\bullet\) Exercise 313
Suppose \(P_i\) is a picture function on a set \(S_i\) for \(i = 1, . . . , k\). We define the picture of a \(k\)-tuple \((x_1, x_2, . . . , x_k)\) to be the product of the pictures of its elements, i.e.
\(\hat{P}((x_1, x_2, . . . x_k)) = \prod_{i=1}^{k} P_i(x_i)\).
How does the picture enumerator \(E_{\hat{P}}\) of the set \(S_1 \times S_2 \times · · · \times S_k\) of all \(k\)-tuples with \(x_i ∈ S_i\) relate to the picture enumerators of the sets \(S_i\)? In the special case that \(S_i = S\) for all \(i\) and \(P_i = P\) for all \(i\), what is \(E_{\hat{P}} (S^k)\)?
\(\bullet\) Exercise \(314\)
Use the Orbit-Fixed Point Theorem to determine the Orbit Enumerator for the colorings, with two colors (red and blue), of six circles placed at the vertices of a hexagon which is free to move in the plane. Compare the coefficients of the resulting polynomial with the various orbits you found in Problem 310.
Exercise \(315\)
Find the generating function (in variables \(R\), \(B\)) for colorings of the faces of a cube with two colors (red and blue). What does the generating function tell you about the number of ways to color the cube (up to spatial movement) with various combinations of the two colors?
6.3.2: The Pólya-Redfield Theorem
Pólya’s (and Redfield’s) famed enumeration theorem deals with situations such as those in Problems 314 and 315 in which we want a generating function for the set of all colorings a set \(S\) using a set \(T\) of colors, where the picture of a coloring is the product of the multiset of colors it uses. We are again thinking of the colors as variables. The point of the next series of problems is to analyze the solutions to Problems 314 and 315 in order to see what Pólya and Redfield saw (though they didn’t see it in this notation or using this terminology).
\(\bullet\) Exercise \(316\)
In Problem 314 we have four kinds of group elements: the identity (which fixes every coloring), the rotations through \(60\) or \(300\) degrees, the rotations through \(120\) and \(240\) degrees, and the rotation through \(180\) degrees. The fixed point enumerator for the rotation group acting on the colorings of the hexagon is by definition the sum of the fixed point enumerators of colorings fixed by the identity, of colorings fixed by \(60\) or \(300\) degree rotations, of colorings fixed by \(120\) or \(240\) degree rotations, and of colorings fixed by the \(180\) degree rotation. To the extent that you haven’t already done it in an earlier problem, write down each of these enumerators (one for each kind of permutation) individually and factor each one (over the integers) as completely as you can.
\(\bullet\) Exercise \(317\)
In Problem 315 we have five different kinds of group elements. For each kind of element, to the extent that you haven’t already done it in an earlier problem, write down the fixed point enumerator for the elements of that kind. Factor the enumerators as completely as you can.
\(\bullet\) Exercise \(318\)
In Problem 316, each “kind” of group element has a “kind” of cycle structure. For example, a rotation through \(180\) degrees has three cycles of size two. What kind of cycle decomposition does a rotation through \(60\) or \(300\) degrees have? What kind of cycle decomposition does a rotation through \(120\) or \(240\) degrees have? Discuss the relationship between the cycle structures and the factored enumerators of fixed points of the permutations in Problem 316. Recall that we said that a group of permutations acts on a set \(S\) if, for each member \(σ\) of \(G\) there is a permutation \(\overline{σ}\) of \(S\) such that
\(\widehat{σ ◦ \varphi} = \hat{σ} ◦ \hat{\varphi}\)
for all members \(σ\) and \(\varphi\) of \(G\). Since \(σ\) is a permutation of \(S\), \(σ\) has a cycle decomposition as a permutation of \(S\) (as well as whatever its cycle decomposition is in the original permutation group \(G\)).
\(\bullet\) Exercise \(319\)
In Problem 317, each “kind” of group element has a “kind” of cycle decomposition in the action of the rotation group of the cube on the faces of the cube. For example, a rotation of the cube through \(180\) degrees around a vertical axis through the centers of the top and bottom faces has two cycles of size two and two cycles of size one.
To the extent that you haven’t already done it in an earlier problem, answer the following questions. How many such rotations does the group have? What are the other “kinds” of group elements, and what are their cycle structures? Discuss the relationship between the cycle decomposition and the factored enumerator in Problem 317.
\(\bullet\) Exercise \(320\)
The usual way of describing the Pólya-Redfield enumeration theorem involves the “cycle indicator” or “cycle index” of a group acting on a set. Suppose we have a group \(G\) acting on a finite set \(S\). Since each group element \(σ\) gives us a permutation \(\overline{σ}\) of \(S\), as such it has a decomposition into disjoint cycles as a permutation of \(S\). Suppose \(σ\) has \(c_1\) cycles of size \(1\), \(c_2\) cycles of size \(2, ..., c_n\) cycles of size \(n\). Then the cycle monomial of \(σ\) is
\(z(σ) = z_1^{c^1} z_2^{c^2} · · · z_n^{c^n}\).
The cycle indicator or cycle index of \(G\) acting on \(S\) is
\(Z(G, S) = \dfrac{1}{|G|} \sum_{σ:σ∈G} z(σ)\).
- What is the cycle index for the group \(D_6\) acting on the vertices of a hexagon?
- What is the cycle index for the group of rotations of the cube acting on the faces of the cube?
Exercise \(321\)
How can you compute the Orbit Enumerator of \(G\) acting on colorings of \(S\) by a finite set \(T\) of colors from the cycle index of \(G\) acting on \(S\)? (Use \(t\), thought of as a variable, as the picture of an element \(t\) of \(T\).) State and prove the relevant theorem! This is Pólya’s and Redfield’s famous enumeration theorem.
\(\rightarrow\) Exercise \(322\)
Suppose we make a necklace by stringing \(12\) pieces of brightly colored plastic tubing onto a string and fastening the ends of the string together. We have ample supplies of blue, green, red, and yellow tubing available. Give a generating function in which the coefficient of \(B^iG^jR^kY^h\) is the number of necklaces we can make with \(i\) blues, \(j\) greens, \(k\) reds, and \(h\) yellows. How many terms would this generating function have if you expanded it in terms of powers of \(B\), \(G\), \(R\), and \(Y\)? Does it make sense to do this expansion? How many of these necklaces have \(3\) blues, \(3\) greens, \(2\) reds, and \(4\) yellows?
Exercise \(323\)
What should we substitute for the variables representing colors in the orbit enumerator of \(G\) acting on the set of colorings of \(S\) by a set \(T\) of colors in order to compute the total number of orbits of \(G\) acting on the set of colorings? What should we substitute into the variables in the cycle index of a group \(G\) acting on a set \(S\) in order to compute the total number of orbits of \(G\) acting on the colorings of \(S\) by a set \(T\)? Find the number of ways to color the faces of a cube with four colors.
\(\rightarrow\) Exercise \(324\)
We have red, green, and blue sticks all of the same length, with a dozen sticks of each color. We are going to make the skeleton of a cube by taking eight identical lumps of modeling clay and pushing three sticks into each lump so that the lumps become the vertices of the cube. (Clearly, we won’t need all the sticks!) In how many different ways could we make our cube? How many cubes have four edges of each color? How many have two red, four green, and six blue edges?
\(\rightarrow\) Exercise \(325\)
How many cubes can we make in Problem 324 if the lumps of modeling clay can be any of four colors?
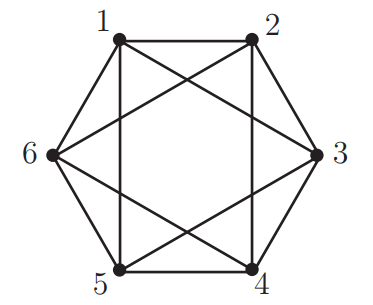
\(\rightarrow\) Exercise \(326\)
In Figure 6.3.2 we see a graph with six vertices. Suppose we have three different kinds of computers that can be placed at the six vertices of the graph to form a network. In how many different ways may the computers be placed? (Two graphs are not different if we can redraw one of the graphs so that it is identical to the other one.) This is equivalent to permuting the vertices in some way so that when we apply the permutation to the endpoints of the edges to get a new edge set, the new edge set is equal to the old one. Such a permutation is called an automorphism of the graph. Then two computer placements are the same if there is an automorphism of the graph that carries one to the other. (Hint).
\(\rightarrow\) Exercise \(327\)
Two simple graphs on the set \([n] = \{1, 2, . . . , n\}\) with edge sets \(E\) and \(E'\) (which we think of as sets of two-element sets for this problem) are said to be isomorphic if there is a permutation \(σ\) of \([n]\) which, in its action of two-element sets, carries \(E\) to \(E'\). We say two graphs are different if they are not isomorphic. Thus the number of different graphs is the number of orbits of the set of all sets of two-element subsets of \([n]\) under the action of the group \(S_n\). We can represent an edge set by its characteristic function (as in problem 33). That is, we define
\(χ_E(\{u, v\})=\left\{ \begin{array}{ll} 1 \text{ if } \{u, v\} ∈ E\\ 0 \text{ otherwise.} \end{array} \right. \)
Thus we can think of the set of graphs as a set of colorings with colors \(0\) and \(1\) of the set of all two-element subsets of \([n]\). The number of different graphs with vertex set \([n]\) is thus the number of orbits of this set of colorings under the action of the symmetric group \(S_n\) on the set of two-element subsets of \([n]\). Use this to find the number of different graphs on five vertices. (Hint).
Notes
1. There is a fascinating subtle issue of what makes two molecules different. For example, suppose we have a molecule in the form of a cube, with one atom at each vertex. If we interchange the top and bottom faces of the cube, each atom is still connected to exactly the same atoms as before. However, we cannot achieve this permutation of the vertices by a member of the rotation group of the cube. It could well be that the two versions of the molecule interact with other molecules in different ways, in which case we would consider them chemically different. On the other hand, if the two versions interact with other molecules in the same way, we would have no reason to consider them chemically different. This kind of symmetry is an example of what is called chirality in chemistry.


