5.3: Deletion-Contraction and the Chromatic Polynomial
- Page ID
- 6117
\(\rightarrow\) Exercise 243
In Chapter 2 we introduced the deletion-contraction recurrence for counting spanning trees of a graph. Figure out how the chromatic polynomial of a graph is related to those resulting from deletion of an edge \(e\) and from contraction of that same edge \(e\). Try to find a recurrence like the one for counting spanning trees that expresses the chromatic polynomial of a graph in terms of the chromatic polynomials of \(G − e\) and \(G/e\) for an arbitrary edge \(e\). Use this recurrence to give another proof that the number of ways to color a graph with \(x\) colors is a polynomial function of \(x\). (Hint).
Exercise 244
Use the deletion-contraction recurrence to reduce the computation of the chromatic polynomial of the graph in Figure 5.3.1 to computation of chromatic polynomials that you can easily compute. (You can simplify your computations by thinking about the effect on the chromatic polynomial of deleting an edge that is a loop, or deleting one of several edges between the same two vertices.)
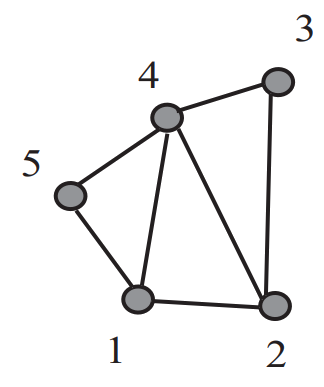
\(\rightarrow\) Exercise 245
- In how many ways may you properly color the vertices of a path on \(n\) vertices with \(x\) colors? Describe any dependence of the chromatic polynomial of a path on the number of vertices.
- (Not tremendously hard.) In how many ways may you properly color the vertices of a cycle on \(n\) vertices with \(x\) colors? Describe any dependence of the chromatic polynomial of a cycle on the number of vertices.
Exercise 246
In how many ways may you properly color the vertices of a tree on \(n\) vertices with \(x\) colors? (Hint).
\(\rightarrow\) Exercise 247
What do you observe about the signs of the coefficients of the chromatic polynomial of the graph in Figure 5.3.1? What about the signs of the coefficients of the chromatic polynomial of a path? Of a cycle? Of a tree? Make a conjecture about the signs of the coefficients of a chromatic polynomial and prove it.


