5.3: Hamilton Cycles and Paths
- Page ID
- 7168
Here is a problem similar to the Königsberg Bridges problem: suppose a number of cities are connected by a network of roads. Is it possible to visit all the cities exactly once, without traveling any road twice? We assume that these roads do not intersect except at the cities. Again there are two versions of this problem, depending on whether we want to end at the same city in which we started.
This problem can be represented by a graph: the vertices represent cities, the edges represent the roads. We want to know if this graph has a cycle, or path, that uses every vertex exactly once. (Recall that a cycle in a graph is a subgraph that is a cycle, and a path is a subgraph that is a path.) There is no benefit or drawback to loops and multiple edges in this context: loops can never be used in a Hamilton cycle or path (except in the trivial case of a graph with a single vertex), and at most one of the edges between two vertices can be used. So we assume for this discussion that all graphs are simple.
A cycle that uses every vertex in a graph exactly once is called a Hamilton cycle, and a path that uses every vertex in a graph exactly once is called a Hamilton path.
Unfortunately, this problem is much more difficult than the corresponding Euler circuit and walk problems; there is no good characterization of graphs with Hamilton paths and cycles. Note that if a graph has a Hamilton cycle then it also has a Hamilton path.
There are some useful conditions that imply the existence of a Hamilton cycle or path, which typically say in some form that there are many edges in the graph. An extreme example is the complete graph \(K_n\): it has as many edges as any simple graph on \(n\) vertices can have, and it has many Hamilton cycles. The problem for a characterization is that there are graphs with Hamilton cycles that do not have very many edges. The simplest is a cycle, \(C_n\): this has only \(n\) edges but has a Hamilton cycle. On the other hand, Figure \(\PageIndex{1}\) shows graphs with just a few more edges than the cycle on the same number of vertices, but without Hamilton cycles.

There are also graphs that seem to have many edges, yet have no Hamilton cycle, as indicated in Figure \(\PageIndex{2}\).
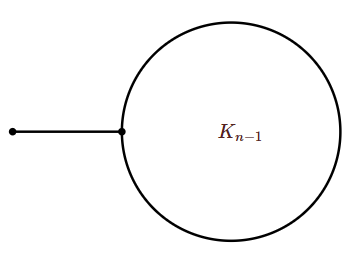
The key to a successful condition sufficient to guarantee the existence of a Hamilton cycle is to require many edges at lots of vertices.
If \(G\) is a simple graph on \(n\) vertices, \(n\ge3\), and \(\text{d}(v)+\text{d}(w)\ge n\) whenever \(v\) and \(w\) are not adjacent, then \(G\) has a Hamilton cycle.
- Proof
-
First we show that \(G\) is connected. If not, let \(v\) and \(w\) be vertices in two different connected components of \(G\), and suppose the components have \(n_1\) and \(n_2\) vertices. Then \(\text{d}(v)\le n_1-1\) and \(\text{d}(w)\le n_2-1\), so \(\text{d}(v)+\text{d}(w)\le n_1+n_2-2< n\). But since \(v\) and \(w\) are not adjacent, this is a contradiction.
Now consider a longest possible path in \(G\): \(v_1,v_2,\ldots,v_k\). Suppose, for a contradiction, that \(k< n\), so there is some vertex \(w\) adjacent to one of \(v_2,v_3,\ldots,v_{k-1}\), say to \(v_i\). If \(v_1\) is adjacent to \(v_k\), then \(w,v_i,v_{i+1},\ldots,v_k,v_1,v_2,\ldots v_{i-1}\) is a path of length \(k+1\), a contradiction. Hence, \(v_1\) is not adjacent to \(v_k\), and so \(\text{d}(v_1)+\text{d}(v_k)\ge n\). The neighbors of \(v_1\) are among \(\{v_2,v_3,\ldots,v_{k-1}\}\) as are the neighbors of \(v_k\). Consider the vertices \[W=\{v_{l+1}\mid v_{l} \hbox{ is a neighbor of \(v_k\)}\}.\nonumber\] Then \(|N(v_k)|=|W|\) and \(W\subseteq \{v_3,v_4,\ldots,v_k\}\) and \(N(v_1)\subseteq \{v_2,v_3,\ldots,v_{k-1}\}\), so \(W\cup N(v_1)\subseteq \{v_2,v_3,\ldots,v_{k}\}\), a set with \(k-1< n\) elements. Since \(|N(v_1)|+|W|=|N(v_1)|+|N(v_k)|\ge n\), \(N(v_1)\) and \(W\) must have a common element, \(v_j\); note that \(3\le j\le k-1\). Then this is a cycle of length \(k\): \[v_1,v_j,v_{j+1},\ldots,v_k,v_{j-1},v_{j-2},\ldots,v_1.\nonumber\] We can relabel the vertices for convenience: \[v_1=w_1,w_2,\ldots,w_k=v_2,w_1.\nonumber\] Now as before, \(w\) is adjacent to some \(w_l\), and \(w,w_l,w_{l+1},\ldots,w_k,w_1,w_2,\ldots w_{l-1}\) is a path of length \(k+1\), a contradiction. Thus, \(k=n\), and, renumbering the vertices for convenience, we have a Hamilton path \(v_1,v_2,\ldots,v_n\). If \(v_1\) is adjacent to \(v_n\), there is a Hamilton cycle, as desired.
If \(v_1\) is not adjacent to \(v_n\), the neighbors of \(v_1\) are among \(\{v_2,v_3,\ldots,v_{n-1}\}\) as are the neighbors of \(v_n\). Consider the vertices \[W=\{v_{l+1}\mid v_l \hbox{ is a neighbor of \(v_n\)}\}.\nonumber\] Then \(|N(v_n)|=|W|\) and \(W\subseteq \{v_3,v_4,\ldots,v_n\}\), and \(N(v_1)\subseteq \{v_2,v_3,\ldots,v_{n-1}\}\), so \(W\cup N(v_1)\subseteq \{v_2,v_3,\ldots,v_{n}\}\), a set with \(n-1< n\) elements. Since \(|N(v_1)|+|W|=|N(v_1)|+|N(v_k)|\ge n\), \(N(v_1)\) and \(W\) must have a common element, \(v_i\); note that \(3\le i\le n-1\). Then this is a cycle of length \(n\): \[v_1,v_i,v_{i+1},\ldots,v_k,v_{i-1},v_{i-2},\ldots,v_1,\nonumber\] and is a Hamilton cycle.
The property used in this theorem is called the Ore property; if a graph has the Ore property it also has a Hamilton path, but we can weaken the condition slightly if our goal is to show there is a Hamilton path. The proof of this theorem is nearly identical to the preceding proof.
If \(G\) is a simple graph on \(n\) vertices and \(\text{d}(v)+\text{d}(w)\ge n-1\) whenever \(v\) and \(w\) are not adjacent, then \(G\) has a Hamilton path.
Suppose \(G\) is not simple. The existence of multiple edges and loops can't help produce a Hamilton cycle when \(n\geq 3\): if we use a second edge between two vertices, or use a loop, we have repeated a vertex. To extend the Ore theorem to multigraphs, we consider the condensation of \(G\): When \(n≥3\), the condensation of \(G\) is simple, and has a Hamilton cycle if and only if \(G\) has a Hamilton cycle. So if the condensation of \(G\) satisfies the Ore property, then \(G\) has a Hamilton cycle.


