6.1: Prelude to Pólya–Redfield Counting
- Page ID
- 7173
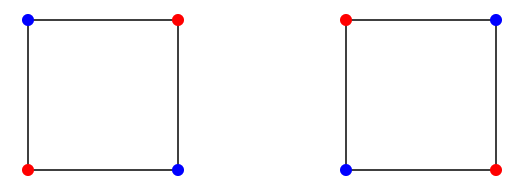
We have talked about the number of ways to properly color a graph with \(k\) colors, given by the chromatic polynomial. For example, the chromatic polynomial for the graph in Figure \(\PageIndex{1}\) is \(k^4 - 4k^3 + 6k^2 - 3k\), and \(f(2)=2\). The two colorings are shown in the figure, but in an obvious sense they are the same coloring, since one can be turned into the other by simply rotating the graph. We will consider a slightly different sort of coloring problem, in which we count the "truly different'' colorings of objects.
Many of the "objects'' we color will appear to be graphs, but we will usually be interested in them as geometric objects rather than graphs, and we will not require that adjacent vertices be different colors. This will simplify the problems; counting the number of different proper colorings of graphs can also be done, but it is more complicated.
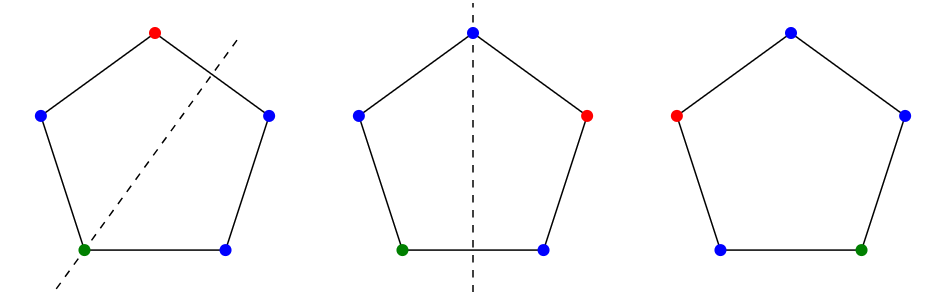
So consider this problem: How many different ways are there to color the vertices of a regular pentagon with \(k\) colors? The number of ways to color the vertices of a fixed pentagon is \(k^5\), but this includes many duplicates, that is, colorings that are really the same. But what do we mean by "the same'' in this case? We might mean that two colorings are the same if we can rotate one to get the other. But what about the colorings in Figure \(\PageIndex{2}\)? Are they the same? Neither can be rotated to produce the other, but either can be flipped or reflected through a vertical line to produce the other. In fact we are free to decide what "the same'' means, but we will need to make sure that our requirements are consistent.
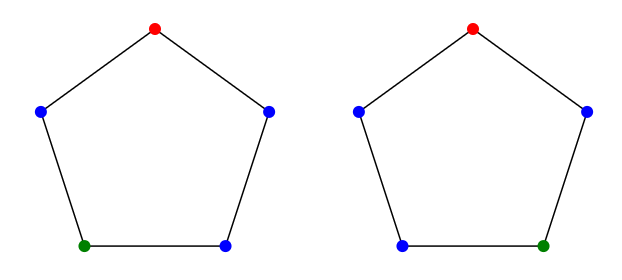
As an example of what can go wrong if we're not careful, note that there are five lines through which the pentagon can be reflected onto itself. Suppose we want to consider colorings to be "the same'' if one can be produced from the other by a reflection, but not if one can be obtained from the other by rotation. Surely if one coloring can be obtained by two reflections in a row from another, then these colorings should also be the same. But two reflections in a row equal a rotation, as shown in Figure \(\PageIndex{3}\). So whenever we have some motions that identify two colorings, we are required to include all combinations of the motions as well. In addition, any time we include a motion, we must include the "inverse'' motion. For example, if we say a rotation by \(54^\circ\) degrees produces a coloring that we consider to be the same, a rotation by \(-54^\circ\) must be included as well (we may think of this as a rotation by \(306^\circ\)). Finally, since any coloring is the same as itself, we must always include the "trivial'' motion, namely, doing nothing, or rotation by \(0^\circ\) if you prefer.