12.1: Directed Graphs

Last updated
Save as PDF

Page ID: 60133

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Some networks include connections that only allow travel in one direction (one-way roads; transmitters that are not receivers, etc.). These can be modeled using directed graphs.

Definition: Directed Graph

A directed graph, or digraph for short, consists of two sets:

$V$, whose elements are the vertices of the digraph; and

$A$, whose elements are ordered pairs from $V$, so

\[A ⊆ \{(v_1, v_2) | v_1, v_2 ∈ V \}.\]

The elements of $A$ are referred to as the arcs of the digraph.

When drawing a digraph, we draw an arrow on each arc so that it points from the first vertex of the ordered pair to the second vertex.

Like multigraphs, we will not study digraphs in this course, but you should be aware of the basic definition. Many of the results we will cover in this course, generalise to the context of digraphs.

Example $\PageIndex{1}$

A digraph.

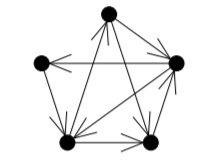
$clipboard_e6cb79bb5779a462e26e7c4aecb4ba311.png$

We will give one example of generalising a result on graphs, to the context of digraphs. In order to do so, we need a definition.

Definition: Word

The outvalency or outdegree of a vertex $v$ in a digraph is the number of arcs whose first entry is $v$, i.e.,

\[ |\{w ∈ V | (v, w) ∈ A\}|. \]

The invalency or indegree of a vertex $v$ in a digraph is the number of arcs whose second entry is $v$.

Notation

The outvalency of vertex $v$ is denoted by $d^+(v)$. The invalency of vertex $v$ is denoted by $d^−(v)$.

Lemma $\PageIndex{1}$: Euler's Handshaking Lemma For Digraphs

For any digraph,

\[\sum_{v∈V} d^+(v) = \sum_{v∈V} d^-(v) = |A|. \]

Proof: For the left-hand side of the equation, at every vertex we count the number of arcs that begin at that vertex. Since each of these arcs ends at some vertex, we get the same result in the middle part of the equation, where at every vertex we count the number of arcs that end at that vertex. In each case, we have counted every arc precisely once, so both of these values are equal to the right-hand side of the equation, the number of arcs in the digraph.

Exercise $\PageIndex{1}$

Use induction to prove Euler’s handshaking lemma for digraphs that have no loops (arcs of the form ($v$, $v$) or multiarcs (more than one arc from some vertex $u$ to some other vertex $v$).
A digraph isomorphism is a bijection on the vertices that preserves the arcs. Come up with a digraph invariant, and prove that it is an invariant.
List the indegree and outdegree of each vertex of the digraph from Example 12.1.1