18.3: Affine Planes

Last updated
Save as PDF

Page ID: 60169

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

You are probably familiar with at least some of Euclid’s axioms of geometry. The following are amongst Euclid’s axioms (we have not used the same terms Euclid used in his Elements, but commonly-used statements that are equivalent to Euclid’s):

Key Euclidian Axioms:

Any two points determine (and so lie together on) a unique line.
(Parallel postulate) For any line $L$, and any point p that does not lie on the line $L$, there is a unique line $L'$ through $p$ that is parallel to $L$; that is, $L$ and $L'$ have no points in common.

If you haven’t taken geometry classes in university, you may not know that we can apply these axioms to finite sets of points, and discover structures that we call finite Euclidean geometries, or more commonly, affine planes. To avoid some trivial situations, we also require that the structure has at least three points, and that not all of the points lie on a single line.

The following definition probably seems obvious.

Definition: Parallel

We say that two lines are parallel if no point lies on both lines.

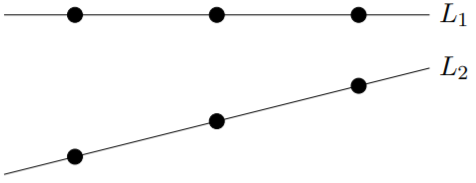
We’ve made special note of this definition because in the finite case, “parallel” lines might be drawn in such a way that they don’t look parallel according to our usual understanding of the term. Since each line has only a finite number of points on it, two lines $L_1$ and $L_2$ are parallel as long as none of the points on $L_1$ also lies on $L_2$, even if in a particular drawing in appears that these lines will meet if we extend them. In the figure below, lines $L_1$ and $L_2$ have three points each, and the lines are parallel.

$clipboard_e2e4b4e7281913f6bf985520797d99f13.png$

Definition: Affine Plane

A (finite) affine plane consists of a (finite) set of points, a (finite) set of lines, and an incidence relation between the points and the lines. The incidence relation must satisfy these Euclidean axioms:

Any two points lie together on a unique line.
For any line $L$, and any point $p$ that does not lie on the line $L$, there is a unique line $L'$ that passes through $p$ and is disjoint from $L$ (that is, it is parallel to $L$).
There are at least three points that are not all on the same line.

For the purposes of this book, we will only consider finite affine planes, so assume from now on that the set of points is finite. It is not very obvious, but the parallel postulate (together with the final axiom) ensure that it is not possible to have a line that doesn’t contain any points, so the set of lines will also be finite.

There is a very nice bijective argument that can be used to show that the number of points on any two lines is equal. Before presenting this, we show that there cannot be a line that contains only one point.

Proposition $\PageIndex{1}$

In a finite affine plane, no line contains only one point.

Proof

The following diagram may be a helpful visual aid as you read through the proof below.

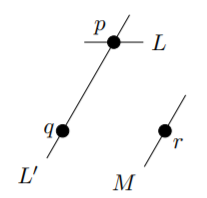
$clipboard_e47a527208048e8a2f82f7d9319acb2be.png$

Towards a contradiction, suppose that there were a line $L$ that contained only a single point, $p$. By the final axiom, there are at least two other points in the finite affine plane, $q$ and $r$, that do not both lie on a line with $p$. By the first axiom, there is a line $L'$ that contains both $p$ and $q$ (but by our choice of $q$ and $r$, $L,$ does not contain $r$). Now by the parallel postulate, there is a line $M$ through $r$ that is parallel to $L'$. Furthermore, there is a unique line through $p$ that is parallel to $M$. But we know that M is parallel to $L'$; in addition, $M$ does not contain $p$, so it is also parallel to $L$; this is a contradiction.

We can now show that every line contains the same number of points.

Proposition $\PageIndex{2}$

In a finite affine plane, if one line contains exactly $n$ points, then every line contains exactly $n$ points.

Proof

Again, we begin with a diagram that may be a helpful visual aid to understanding this proof.

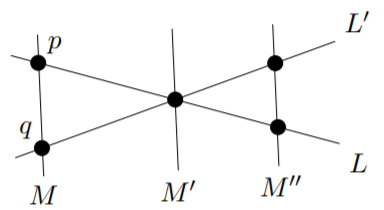
$clipboard_e32fdf0c5f53f7ec8d3c348276bd0c535.png$

Let $L$ be a line that contains exactly $n$ points, and let $L'$ be any other line of the finite affine plane. By Proposition 18.3.1, we know that $n > 1$, and that $L'$ also contains at least two points (we observed above that no line can be empty of points). Since any two points lie together on a unique line, if $L$ and $L'$ meet, they meet in a single point, so there is a point $p$ of $L$ that is not in $L'$, and a point $q$ of $L'$ that is not in $L$. By the first axiom, there is a line $M$ that contains the points $p$ and $q$.

We define a map $ψ$ from points of $L$ to points of $L'$ as follows. Let $ψ(p) = q$. For any other point $p'$ of $L$ (with $p' \neq p$), by the parallel postulate there is a unique line $M'$ through $p'$ that is parallel to $M$. Since $M$ passes through $q$ and is parallel to $M'$, it is the unique line with this property, so in particular, $L'$ cannot be parallel to $M'$. Therefore, $M'$ has a unique point of intersection, say $q'$, with $L'$. Define $ψ(p') = q'$. Since $M'$ and $q'$ were uniquely determined, the map $ψ$ is well-defined (that is, there is no ambiguity about which point of $L'$ is found to be $ψ(p')$).

We claim that $ψ$ is a bijection between the points of $L$ and the points of $L'$; proving this will complete the proof. We first show that $ψ$ is one-to-one. Suppose that $ψ(p_1) = q_1$, $ψ(p_2) = q_2$, and $q_1$ and $q_2$ are actually the same point of $L'$. Then by the definition of $ψ$, $q_1$ is on some line $M_1$ that is parallel to $M$, and contains $p_1$, while $q_2$ is on some line $M_2$ that is parallel to $M$, and contains $p_2$. Since $q_1 = q_2$, the parallel postulate tells us that we must have $M_1 = M_2$. This line can only meet $L$ in a single point, so we must have $p_1 = p_2$. Thus, $ψ$ is one-to-one.

To show that $ψ$ is onto, let $q''$ be any point of $L'$ with $q'' \neq q$ (we already know that $q$ has a pre-image, $p$). By the parallel postulate, there is a unique line $M''$ through $q''$ that is parallel to $M$. Since $M$ is the unique line through $p$ that is parallel to $M''$, we see that $L$ is not parallel to $M''$, so $L$ must meet $M''$ at some point that we will call $p''$. Now by the definition of $ψ$, we have $ψ(p'') = q''$. Thus, $q''$ has a pre-image, so $ψ$ is onto.

We refer to the number of points on each line of a finite affine plane as the order of the plane. We can now figure out how many points are in a finite affine plane of order $n$.

Proposition $\PageIndex{3}$

A finite affine plane of order $n$ has $n^2$ points.

Proof

Since the plane has at least three points, not all of which lie on the same line, it has at least two lines $L$ and $L'$ that intersect at a point q but are not equal. We know that each of these lines contains $n$ points. By the parallel postulate, for each of the $n − 1$ points on $L'$ that is not on $L$, there is a line through that point that is parallel to $L$. Now, $L$ and these $n−1$ lines that are parallel to $L$ each contain n points, and since they are all parallel (it is an exercise, see below, to prove that if $M$ is parallel to $L$ and $N$ is parallel to $L$, then $N$ is parallel to $M$), these points are all distinct. Therefore the plane has at least $n^2$ points.

Consider any point $p$ that is not on $L$. By the parallel postulate, there must be a line $P$ through $p$ that is parallel to $L$. Now, $L$ is the unique line through $q$ that is parallel to $P$, so in particular, $L'$ is not parallel to $P$. Therefore, $L'$ and $P$ have a point of intersection, which is one of the $n − 1$ points of $L'$ that is not on $L$. So $P$ was one of the $n − 1$ lines that we found in our first paragraph, meaning that $p$ is one of the $n^2$ points that we found there. Thus, the plane has exactly $n^2$ points.

You might be wondering by now why we are spending so much time looking at affine planes, when they are a geometric structure. Despite the fact that they come from geometry, finite affine planes can be thought of as a special kind of design.

Think of the points of a finite affine plane as points of a design, and the lines as blocks, with a point being in a block if it is incident with (on) the corresponding line. The first axiom for the incidence relation guarantees that every pair of points appear together in exactly one block, so our design has $λ = 1$. By Proposition 18.3.2, we see that an affine plane of order $n$ is uniform, with $k = n$. By Proposition 18.3.3, an affine plane of order $n$ has $v = n^2$. Although we have not included a proof of this, it can also be shown that this design is regular, so it is in fact a BIBD$(n^2 , n, 1)$.

Using

\[b \binom{k}{t} = λ \binom{v}{t} \]

from Theorem 18.2.1, we see that in a finite affine plane of order $n$ looked at as a design, we have $b \binom{n}{2} = \binom{n^2}{2} $, so $bn(n − 1) = n^2(n^2 − 1)$. Hence $b = n(n + 1)$. In other words, a finite affine plane of order $n$ has $n(n + 1)$ lines.

Example $\PageIndex{1}$

A finite affine plane of order $3$ has $3^2 = 9$ points. Each line has $3$ points, and there are $3(4) = 12$ lines. Since each line has three points, every line lies in a parallel class consisting of three mutually parallel lines, so there are four such parallel classes. We can choose two of the parallel classes of lines to be “horizontal” and “vertical” lines. The other two classes will be the two types of diagonal lines. We can’t draw all of these as straight lines, so we have drawn one parallel class of lines as sets of three points joined by dashes, and the other as sets of three points joined by dots.

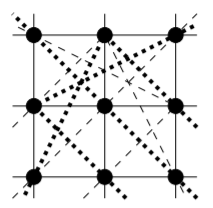
$clipboard_efee7bf8cdba384e9daf01aca685ba13b.png$

The dashes and dots that join sets of points that aren’t in a straight line may not provide a very clear image of what’s going on; it is probably clearer to think of the diagonal lines as “wrapping around” when they go off the bottom, top, or either side of the image, and reappearing on the opposite side.

There is a nice connection between affine planes and mutually orthogonal Latin squares.

Theorem $\PageIndex{1}$

There is an affine plane of order $n > 1$ if and only if there are $n−1$ mutually orthogonal Latin squares of order $n$.

Proof

$(⇒)$ An affine plane of order $n$ has $n+ 1$ classes of parallel lines (each class containing $n$ lines). Consider two of these sets as the horizontal lines and the vertical lines: $H_1, . . . , H_n$ and $V_1, . . . , V_n$. Label a point as $(i, j)$ if it lies at the intersection of $V_i$ and $H_j$. Since each of the $n^2$ points lies on a vertical line and on a horizontal line, and since every pair of points lie together on only one line, this is actually a bijection between $\{1, . . . , n\} \times \{1, . . . , n\}$ and the points of the affine plane; that is, this provides $n^2$ coordinates that uniquely determine the $n^2$ points of the plane.

Consider any one of the remaining parallel classes of $n$ lines, $L_1, . . . , L_n$. Observe that every point of the affine plane lies on precisely one of these lines. Create a Latin square from this parallel class by placing $k$ in position $(i, j)$ of the Latin square if and only if the point $(i, j)$ of the affine plane lies on line $L_k$. Since every line of $L_1, . . . , L_n$ meets every line of $H_1, . . . , H_n$ exactly once (by the axioms of an affine plane), each entry will appear exactly once in each row. Similarly, since every line of $L_1, . . . , L_n$ meets every line of $V_1, . . . , V_n$ exactly once (by the axioms of an affine plane), each entry will appear exactly once in each column. So we have indeed created a Latin square.

We will now show that the $n − 1$ Latin squares created by this method (using the $n − 1$ parallel classes of lines that remain after excluding the ones we have designated as horizontal and vertical lines) are mutually orthogonal. We’ll do this by considering two arbitrary Latin squares, $L$ (coming from the lines $L_1, . . . , L_n)$ and $M$ (coming from the lines $M_1, . . . , M_n)$. In position $(i, j)$, the entry of $L$ being $i'$ means that line $L_{i'}$ passes through the point $(i, j)$ (which is the intersection of lines $V_i$ and $H_j$). Similarly, this entry of $M$ being $j'$ means that line $M_{j'}$ passes through the point $(i, j)$ (which is the intersection of lines $V_i$ and $H_j$). Since the lines $L_{i'}$ and $M_{j'}$ have a unique point of intersection, there cannot be any other positions in which the entry of $L$ is $i'$ while the entry of $M$ is $j'$. Thus, each ordered pair $(i', j') ∈ \{1, . . . , n\} \times \{1, . . . , n\}$ must appear in exactly one position as the entries of $L$ and $M$ (in that order), and hence $L$ and $M$ are orthogonal. Since they were arbitrary, we have $n−1$ mutually orthogonal Latin squares.

$(⇐)$ The converse of this proof uses the same idea, in the opposite direction. Given $n − 1$ mutually orthogonal $n$ by $n$ Latin squares, take the $n^2$ coordinate positions to be the points of our affine plane. Define two parallel classes of lines (each containing $n$ lines) to be the points whose first coordinate is equal (so all of the points with first coordinate $1$ form one line, and all of the points with first coordinate $2$ form a second line, etc.), and the points whose second coordinate is equal. Each of the $n−1$ Latin squares determines an additional parallel class of $n$ lines: namely, each line consists of the points for which the entry of the Latin square has some fixed value. Since $n > 1$, there are clearly at least three points that are not all on the same line. We leave it as an exercise to prove that any two points lie together in a unique line and that the parallel postulate is satisfied.

Example $\PageIndex{2}$

Use the formula from the proof of Theorem 16.3.2 to construct $6$ MOLS of order $7$. Use the construction given in the proof of Theorem 18.3.1 to construct an affine plane of order $7$ from your squares.

Solution

The squares will be:

\[ 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\;\;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 0\;\;\;\;\;\;\;\;\;\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 0\; \; 1 \\ 2\; \; 3\; \; 4\; \; 5\; \; 6\;\;0\; \; 1 \;\;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6 \;\; 0\; \; 1\; \; 2\; \; 3 \\ 3\; \; 4\; \; 5\; \; 6\;\;0\; \; 1\;\;2 \;\;\;\;\;\;\;\;\;\;\; 6 \;\; 0\; \; 1\; \; 2\; \; 3\;\;4\; \; 5 \\ 4\; \; 5\; \; 6\;\;0\; \; 1\;\;2 \;\; 3 \;\;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\;\;4\; \; 5\;\;6 \;\; 0 \\ 5\; \; 6\;\;0\; \; 1\;\;2\;\;3\; \; 4 \;\;\;\;\;\;\;\;\;\;\; 3\;\;4\; \; 5\;\;6 \;\; 0\; \; 1\; \; 2 \\
6\;\;0\; \; 1\;\;2\;\;3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\;\; 5\;\; 6 \;\; 0\; \; 1\; \; 2\; \; 3\;\;4 \\[0.5in] 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\;\;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 3\; \; 4\; \; 5\; \; 6 \;\; 0\;\;1\; \; 2 \;\;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6 \;\; 0\; \; 1\; \; 2\; \; 3 \\ 6\;\;0\; \; 1\;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\;\;4\; \; 5\;\;6 \;\; 0 \\ 2\;\;3\; \; 4\; \; 5\; \; 6\;\;0\; \; 1 \;\;\;\;\;\;\;\;\;\;\; 5\;\; 6 \;\; 0\; \; 1\; \; 2\; \; 3\;\;4 \\ 5\; \; 6\;\;0\; \; 1\;\;2\;\;3\; \; 4 \;\;\;\;\;\;\;\;\;\;\; 2\; \; 3\;\;4\; \; 5\;\;6 \;\; 0\;\;1 \\ 1\;\;2\;\;3\; \; 4\;\;5\; \; 6\;\;0 \;\;\;\;\;\;\;\;\;\;\; 6 \;\; 0\; \; 1\; \; 2\;\;3\;\;4\; \; 5 \\ 4\; \; 5 \;\;6\;\;0\; \; 1\;\;2\;\;3\;\;\;\;\;\;\;\;\;\;\; 3\;\;4\; \; 5\;\;6 \;\; 0\; \; 1\; \; 2 \\[0.5in] 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\;\;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 5\; \; 6\;\;0\; \; 1\;\;2\;\;3\; \; 4\;\;\;\;\;\;\;\;\;\;\; 6 \;\; 0\; \; 1\; \; 2\;\;3\;\;4\; \; 5\\ 3\; \; 4\; \; 5\; \; 6 \;\; 0\;\;1\; \; 2 \;\;\;\;\;\;\;\;\;\;\; 5\;\; 6 \;\; 0\; \; 1\; \; 2\; \; 3\;\;4 \\ 1\;\;2\;\;3\; \; 4\;\;5\; \; 6\;\;0\;\;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6 \;\; 0\; \; 1\; \; 2\; \; 3\\ 6\;\;0\; \; 1\;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\;\; 3\;\;4\; \; 5\;\;6 \;\; 0\; \; 1\; \; 2 \\ 4\; \; 5 \;\;6\;\;0\; \; 1\;\;2\;\;3\;\;\;\;\;\;\;\;\;\;\; 2\; \; 3\;\;4\; \; 5\;\;6 \;\; 0\;\;1 \\ 2\;\;3\; \; 4\; \; 5\; \; 6\;\;0\; \; 1 \;\;\;\;\;\;\;\;\;\;\; 1\;\;2\;\;3\; \; 4\;\;5\; \; 6\;\;0 \]

The affine plane will have $7^2 = 49$ points, and we will denote these as ordered pairs $(a, b)$, where $a$, $b ∈ \{1, . . . , 7\}$and consider them to represent the $49$ positions in a $7$ by $7$ Latin square. There will be $7(8) = 56$ lines, in $8$ parallel classes of seven lines each. Although we could draw the affine plane, you’ve already seen from the affine plane of order $3$ that a black-and-white image all of which is pre-drawn can be more confusing than helpful, so instead we will list each of the $56$ lines as a set of $7$ points.

The first parallel class will represent the horizontal rows:

\[\begin{equation} \begin{split} &\{(1, 1),(2, 1),(3, 1),(4, 1),(5, 1),(6, 1),(7, 1)\}, \;\;\;\;&\{(1, 2),(2, 2),(3, 2),(4, 2),(5, 2),(6, 2),(7, 2)\}, \\ &\{(1, 3),(2, 3),(3, 3),(4, 3),(5, 3),(6, 3),(7, 3)\}, \;\;\;\;&\{(1, 4),(2, 4),(3, 4),(4, 4),(5, 4),(6, 4),(7, 4)\}, \\ &\{(1, 5),(2, 5),(3, 5),(4, 5),(5, 5),(6, 5),(7, 5)\}, \;\;\;\;&\{(1, 6),(2, 6),(3, 6),(4, 6),(5, 6),(6, 6),(7, 6)\}, \\ &\{(1, 7),(2, 7),(3, 7),(4, 7),(5, 7),(6, 7),(7, 7)\} \end{split} \end{equation}\]

and similarly the second parallel class will represent the vertical rows:

\[\begin{equation} \begin{split} &\{(1, 1),(1, 2),(1, 3),(1, 4),(1, 5),(1, 6),(1, 7)\},\;\;\;\; &\{(2, 1),(2, 2),(2, 3),(2, 4),(2, 5),(2, 6),(2, 7)\}, \\
&\{(3, 1),(3, 2),(3, 3),(3, 4),(3, 5),(3, 6),(3, 7)\},\;\;\;\; &\{(4, 1),(4, 2),(4, 3),(4, 4),(4, 5),(4, 6),(4, 7)\}, \\ &\{(5, 1),(5, 2),(5, 3),(5, 4),(5, 5),(5, 6),(5, 7)\}, \;\;\;\; &\{(6, 1),(6, 2),(6, 3),(6, 4),(6, 5),(6, 6),(6, 7)\}, \\ &\{(7, 1),(7, 2),(7, 3),(7, 4),(7, 5),(7, 6),(7, 7)\}. \end{split} \end{equation}\]

The remaining six parallel classes will each represent one of the Latin squares. In the next parallel class, the first line consists of all of the points where the entry of the first Latin square is 0; the second consists of all the points where the entry is 1, and so on.

\[\begin{equation} \begin{split} &\{(1, 1),(7, 2),(6, 3),(5, 4),(4, 5),(3, 6),(2, 7)\}, \;\;\;\;&\{(2, 1),(1, 2),(7, 3),(6, 4),(5, 5),(4, 6),(3, 7)\},\\ &\{(3, 1),(2, 2),(1, 3),(7, 4),(6, 5),(5, 6),(4, 7)\}, \;\;\;\;&\{(4, 1),(3, 2),(2, 3),(1, 4),(7, 5),(6, 6),(5, 7)\},\\ &\{(5, 1),(4, 2),(3, 3),(2, 4),(1, 5),(7, 6),(6, 7)\}, \;\;\;\;&\{(6, 1),(5, 2),(4, 3),(3, 4),(2, 5),(1, 6),(7, 7)\},\\ &\{(7, 1),(6, 2),(5, 3),(4, 4),(3, 5),(2, 6),(1, 7)\}. \end{split} \end{equation}\]

The next parallel class comes from the second Latin square (reading across, so the second square is the second one in the first line):

\[\begin{equation} \begin{split} &\{(1, 1),(6, 2),(4, 3),(2, 4),(7, 5),(5, 6),(3, 7)\},\;\;\;\; &\{(2, 1),(7, 2),(5, 3),(3, 4),(1, 5),(6, 6),(4, 7)\}, \\ &\{(3, 1),(1, 2),(6, 3),(4, 4),(2, 5),(7, 6),(5, 7)\},\;\;\;\; &\{(4, 1),(2, 2),(7, 3),(5, 4),(3, 5),(1, 6),(6, 7)\}, \\ &\{(5, 1),(3, 2),(1, 3),(6, 4),(4, 5),(2, 6),(7, 7)\},\;\;\;\; &\{(6, 1),(4, 2),(2, 3),(7, 4),(5, 5),(3, 6),(1, 7)\}, \\ &\{(7, 1),(5, 2),(3, 3),(1, 4),(6, 5),(4, 6),(2, 7)\}. \end{split} \end{equation}\]

From the third Latin square:

\[\begin{equation} \begin{split} &\{(1, 1),(5, 2),(2, 3),(6, 4),(3, 5),(7, 6),(4, 7)\},\;\;\;\; &\{(2, 1),(6, 2),(3, 3),(7, 4),(4, 5),(1, 6),(5, 7)\}, \\ &\{(3, 1),(7, 2),(4, 3),(1, 4),(5, 5),(2, 6),(6, 7)\},\;\;\;\; &\{(4, 1),(1, 2),(5, 3),(2, 4),(6, 5),(3, 6),(7, 7)\}, \\ &\{(5, 1),(2, 2),(6, 3),(3, 4),(7, 5),(4, 6),(1, 7)\},\;\;\;\; &\{(6, 1),(3, 2),(7, 3),(4, 4),(1, 5),(5, 6),(2, 7)\}, \\ &\{(7, 1),(4, 2),(1, 3),(5, 4),(2, 5),(6, 6),(3, 7)\}. \end{split} \end{equation}\]

From the fourth Latin square:

\[\begin{equation} \begin{split} &\{(1, 1),(4, 2),(7, 3),(3, 4),(6, 5),(2, 6),(5, 7)\},\;\;\;\; &\{(2, 1),(5, 2),(1, 3),(4, 4),(7, 5),(3, 6),(6, 7)\},\\
&\{(3, 1),(6, 2),(2, 3),(5, 4),(1, 5),(4, 6),(7, 7)\},\;\;\;\; &\{(4, 1),(7, 2),(3, 3),(6, 4),(2, 5),(5, 6),(1, 7)\},\\ &\{(5, 1),(1, 2),(4, 3),(7, 4),(3, 5),(6, 6),(2, 7)\},\;\;\;\; &\{(6, 1),(2, 2),(5, 3),(1, 4),(4, 5),(7, 6),(3, 7)\},\\ &\{(7, 1),(3, 2),(6, 3),(2, 4),(5, 5),(1, 6),(4, 7)\}. \end{split} \end{equation}\]

From the fifth Latin square:

\[\begin{equation} \begin{split} &\{(1, 1),(3, 2),(5, 3),(7, 4),(2, 5),(4, 6),(6, 7)\},\;\;\;\; &\{(2, 1),(4, 2),(6, 3),(1, 4),(3, 5),(5, 6),(7, 7)\},\\ &\{(3, 1),(5, 2),(7, 3),(2, 4),(4, 5),(6, 6),(1, 7)\},\;\;\;\; &\{(4, 1),(6, 2),(1, 3),(3, 4),(5, 5),(7, 6),(2, 7)\},\\ &\{(5, 1),(7, 2),(2, 3),(4, 4),(6, 5),(1, 6),(3, 7)\},\;\;\;\; &\{(6, 1),(1, 2),(3, 3),(5, 4),(7, 5),(2, 6),(4, 7)\},\\ &\{(7, 1),(2, 2),(4, 3),(6, 4),(1, 5),(3, 6),(5, 7)\}. \end{split} \end{equation}\]

And finally,

\[\begin{equation} \begin{split} &\{(1, 1),(2, 2),(3, 3),(4, 4),(5, 5),(6, 6),(7, 7)\}, \;\;\;\;&\{(2, 1),(3, 2),(4, 3),(5, 4),(6, 5),(7, 6),(1, 7)\},\\
&\{(3, 1),(4, 2),(5, 3),(6, 4),(7, 5),(1, 6),(2, 7)\}, \;\;\;\;&\{(4, 1),(5, 2),(6, 3),(7, 4),(1, 5),(2, 6),(3, 7)\},\\ &\{(5, 1),(6, 2),(7, 3),(1, 4),(2, 5),(3, 6),(4, 7)\}, \;\;\;\;&\{(6, 1),(7, 2),(1, 3),(2, 4),(3, 5),(4, 6),(5, 7)\},\\ &\{(7, 1),(1, 2),(2, 3),(3, 4),(4, 5),(5, 6),(6, 7)\}. \end{split} \end{equation}\]

comes from the sixth Latin square.

Every affine plane that we know of, has as its order some prime power. We have previously seen (through the connection to MOLS) that there are affine planes of every prime order. Many design theorists have tried to answer the question of whether or not the order of an affine plane must always be a prime power, but the answer is not yet known. In fact, it is not currently known whether or not there is an affine plane of order $12$.

Exercise $\PageIndex{1}$

1) Prove that if $L$, $M$, and $N$ are lines of an affine plane, and $L$ is parallel to both $M$ and $N$, then $M$ is parallel to $N$.

2) Draw a finite affine plane of order $5$. How many lines does it have?

3) How many points, and how many lines are in a finite affine plane of order $19$?

4) Prove the omitted details from the proof of Theorem 18.3.1: that is, that the given construction yields a structure that satisfies the axioms of an affine plane.

5) Draw an affine plane of order $5$. Use the construction given in the proof of Theorem 18.3.1 to produce $4$ mutually orthogonal Latin squares of order $5$ from your plane.