18.4: Projective Planes

Last updated
Save as PDF

Page ID: 60170

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A projective plane is another geometric structure (closely related to affine planes). In a finite projective plane, the set of points (and therefore the set of lines) must be finite. Like finite affine planes, finite projective planes can be thought of as a special kind of design.

Definition: Projective Plane

A projective plane consists of a set of points, a set of lines, and an incidence relation between the points and the lines. The incidence relation must satisfy the following conditions:

for any two points, there is a unique line that is incident with both of them;
for any two lines, there is a unique point that is incident with both of them;
there exist four points such that no three are incident with a single line.

As in the case of affine planes, the final axiom has been developed to avoid some trivial situations.

Think of the points of a finite projective plane as points of a design, and the lines as blocks, with a point being in a block if it is incident with the corresponding line. Then the first condition on the incidence relation for a projective plane guarantees that every pair of points appear together in exactly one block.

Example $\PageIndex{1}$

The Fano plane is the most well-known finite projective plane (and also the smallest). Here is a drawing of it. It has $7$ points and $7$ lines, one of which is the circle around the middle.

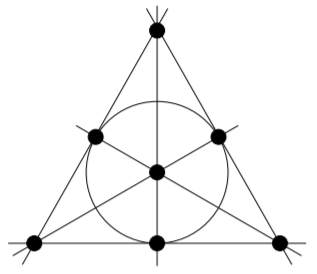
$clipboard_eab7775bce5df7934ded97b40f0d78f29.png$

You have seen this structure already in this course; it is the same as the BIBD$(7, 3, 1)$ that appeared in Example 17.1.1.

The following is a very interesting connection. We will not try to present the proof here, but it is a natural extension of the similar result that we proved for affine planes.

Theorem $\PageIndex{1}$

There is a finite projective plane with $n + 1$ points on each line, if and only if there is a complete set of $n − 1$ MOLS of order $n$.

Exercise $\PageIndex{1}$

1) Is every design with $λ = 1$ a projective plane? If not, what condition could fail?

2) Which (if any) of the designs we have seen in this course, are projective planes?

3) From our results on MOLS, for what values can you be sure that a projective plane exists?

4) From our results on MOLS, for what values can you be sure that a projective plane does not exist?

5) What can you determine about the parameters of a design that corresponds to a projective plane?