4.3: Frequency Analysis
- Page ID
- 28648
\(\newcommand{\RR}{\mathbb R}\)
\(\newcommand{\QQ}{\mathbb Q}\)
\(\newcommand{\ZZ}{\mathbb Z}\)
\(\newcommand{\Cc}{\mathcal C}\)
\(\newcommand{\Dd}{\mathcal D}\)
\(\newcommand{\Ee}{\mathcal E}\)
\(\newcommand{\Ff}{\mathcal F}\)
\(\newcommand{\Kk}{\mathcal K}\)
\(\newcommand{\Mm}{\mathcal M}\)
\(\newcommand{\Pp}{\mathcal P}\)
\(\newcommand{\ind}{\operatorname{ind}}\)
\(\newcommand{\ord}{\operatorname{ord}}\)
The Caesar cipher seems very weak. But looking at a ciphertext, such as
wrehruqrwwrehwkdwlvwkhtxhvwlrq
zkhwkhuwlvqreohulqwkhplqgwrvxiihu
wkhvolqjvdqgduurzvrirxwudjhrxviruwxqh
ruwrwdnhdupvdjdlqvwdvhdriwurxeohv
dqgebrssrvlqjhqgwkhp
it is hard to know where to start – this hardly seems to be English at all.
Perhaps we should start with the Caesar cipher itself, assuming (anachronistically) that Caesar was following Kerckhoff’s Principle, or that (more chronistically) spies had determined the cryptosystem but not the key.
One thing we notice right away is that what we do not know, that key, is such a small thing to be giving us such trouble. In fact, if we tried a random choice of key, nearly four times out of \(100\) (using the modern “Latin alphabet” of \(26\) letters – in Caesar’s time, the actual Latin alphabet had only \(23\), so even better!) would, purely by dumb luck, give us a correct decryption. Formally, we are talking about
Definition: Keyspace
The set of all valid keys for some cryptosystem is called its keyspace.
Example \(\PageIndex{1}\)
The keyspace of the Caesar cipher cryptosystem is the alphabet.
Example \(\PageIndex{2}\)
The keyspace of the Vigenère cipher cryptosystem with a key length of \(\ell\) is all sequences of \(\ell\) letters in the alphabet; therefore, it has \(N^\ell\) elements, if the alphabet is of size \(N\). If the precise key length is not known, but it is known to be less than or equal to some bound \(L\in\NN\), then there are \(\sum_{j=1}^L N^j\) possible keys.
Example \(\PageIndex{3}\)
Any sequence of letters of length \(M\) is a possible key (pad) for a one-time pad encryption of a message of length \(M\). Therefore there are \(N^M\) possible one-time pads for a message of length \(M\) over an alphabet of size \(N\).
We computed the sizes of these various keyspaces because one thing that seemed weak about the Caesar cipher was how small was its keyspace. In fact, a better strategy than simply guessing at random would be to try all possible keys – there are only \(26\) (or \(23\) in Julius’s time)! – and see which one gives the correct decryption. Such an approach is called a brute-force attack [or exhaustive search]. Even in Caesar’s time, the Caesar cipher keyspace is so small that Eve could check all possible keys and see which yielded the cleartext of a message from Alice to Bob.
Things are a little more difficult for the Vigenère cipher. For example, there are nearly \(12\) million keys to try if the key length is known to be five. Before the computer age, this would have been completely intractable. Even in the \(21^{\text{st}}\) century, where it would be nearly instantaneous to human eyes for a computer to generate all of those possible decryption, there is a problem: those human eyes would have to look over the \(12\) million possibilities and pick out which was the valid decryption.
Amazon’s Mechanical Turk (see https://www.mturk.com/mturk/welcome) might be able to marshal enough human eyes to solve a single brute force Vigenère decryption. But a better approach would be to write a computer program that can distinguish gibberish from a real message Alice might have sent to Bob – then, in a matter of moments, a brute force attack would succeed.
If we are to distinguish gibberish from a real message, we need to know what possible real messages are. This motivates the following
Definition: Message Space
The set of possible messages for an encrypted communication is called the message space.
Without some structure for the message space, cryptanalysis can become nearly impossible. For example, if Alice is e-mailing an encrypted version the combination of a safe to Bob, the message space is not too large but has no identifiable features: a brute force attack would have no way of telling which potential decryption was the actual combination.
But suppose we assume that the message space of Alice and Bob’s communication is a set of short (or long, which would be better) English texts. There is quite a bit of structure in English texts – we human speakers of English certainly recognize valid English. The question is whether we can automate the process of detection of valid English texts.
Looking back at the example Caesar encryption given at the beginning of this section, we noticed that it did not look like English – but in what way? One thing was, of course, that it does not have any English words in it. Someone who knows English knows most of the words of that language and can recognize that this text has none of them, except maybe “up” and “i” (several times).
This suggests an approach: take a list of all words in English, with all variant and derivative forms, add in some possible short random sequences that may have been included in otherwise standard English (where Alice was quoting some nonsense she’d heard, or was writing down a graffito she saw on the side of a subway car, etc.), and compare them to possible decryptions of the ciphertext. This scheme is not very practical. But if the message space were small enough, something like this would be reasonable.
Looking back at the message again, another thing that immediately strikes the eye of a reader of English is that it does not seem to have the right letters, or the right combinations of letters. For example, there do not seem to be enough vowels. Looking at how often letters occur in a text compared to what we expect is called frequency analysis. Its use in cryptanalysis was apparently first described by the Muslim philosopher and mathematician al-Kindi1 in his \(9^{\text{th}}\) century work Manuscript on Deciphering Cryptographic Messages.
Here is a table of the frequencies of the letters in a bit of standard English (some of the plays of Shakespeare):
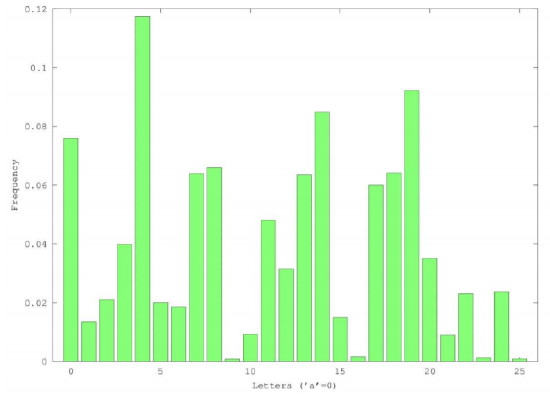
Notice that the letter ‘e’ is the most common, by a bit. So a first cryptanalytic approach using frequency analysis would simply be to use the Caesar decryption key which moved the most frequent letter in the ciphertext to be ‘e’. With the ciphertext at the beginning of this section, that would yield the decryption:
ezmpzcyzeezmpesletdespbfpdetzy
hspespcetdyzmwpctyespxtyoezdfqqpc
espdwtyrdlyolcczhdzqzfeclrpzfdqzcefyp
zcezelvplcxdlrltydeldplzqeczfmwpd
lyomjzaazdtyrpyoespx
Not so good. Apparently looking only at the most frequent letter is insufficient: the most frequent letter in the plaintext of this message was not ’e’.
Instead, let us look at the entire frequency table for this ciphertext.
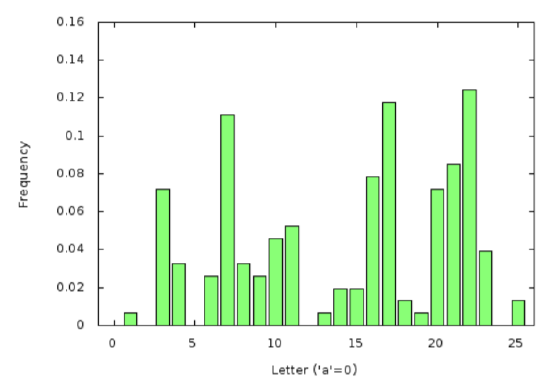
Unfortunately, this is not exactly the standard (Shakespearean) English frequency distribution, nor is it even a shifted (with wrapping past \(25\) back to \(0\)) version of Shakespeare’s distribution. But perhaps one of its shifts is fairly close to Shakespeare.
This suggest the following more refined cryptanalytic approach: try all possible decryptions (which is not so bad for the Caesar cipher, because of its small keyspace) and choose the one whose entire letter frequency table is closest to the standard English letter frequency table – so, not looking only at the most frequent letter, but looking at the whole frequency distribution; and not looking for exact match, but merely for the best approximate match.
Which brings up the question of what is the best way to measure the distance between two distributions. One commonly used approach is to measure the
Definition: Total Square Error
The total square error is a distance between two distributions \(f\) and \(g\) given by \[d(f,g)=\sum_{j=0}^{25} \left(f(j)-g(j)\right)^2\] where we are always working with our distributions defined on the letters in the form ‘\(a\)’\(=0\), ‘\(b\)’\(=1\), etc.).
Minimizing this distance is equivalent to least squares in statistics or linear algebra.
Following this strategy with the ciphertext from the beginning of this section, we get the following
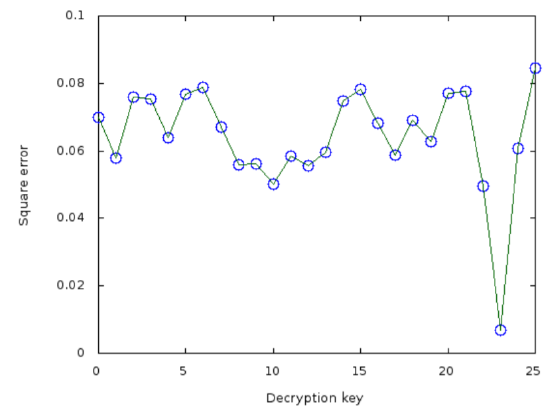
The minimal square error will then come from decryption key \(23\) (corresponding to an original encryption key of \(3\); this was done by Julius himself, anachronistically). The corresponding cleartext then would have been
tobeornottobethatisthequestion
whethertisnoblerinthemindtosuffer
theslingsandarrowsofoutrageousfortune
ortotakearmsagainstaseaoftroubles
andbyopposingendthem
which looks pretty good.
Interestingly, this approach to non-gibberish detection is fairly robust, even with quite short texts which might be expected to have frequency distributions rather far away from the English standard. For example, with ciphertext
rkkrtbrkeffespkyvtifjjifruj
we have
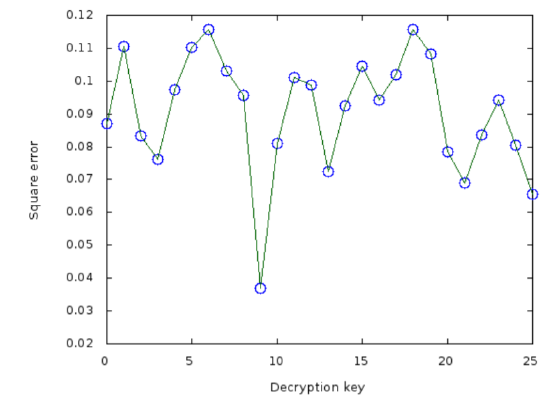
rkkrtbrkeffespkyvtifjjifruj (Copyright; author via source)from which we conclude that the decryption key is \(9\), corresponding to an encryption key of \(17\). Thus the cleartext must have been
attackatnoonbythecrossroads
which seems like the kind of thing Julius might have said.
So much for cryptanalysis of the Caesar cipher. Moving on to Vigenère, the first problem we face is finding out the key length. Because if we knew that key length \(\ell\), we would divide the ciphertext into \(\ell\) shorter texts consisting of every \(\ell^{\text{th}}\) character starting with the first, then with the second, etc., up to starting with the \(\ell^{th}\). Applying the automatic Caesar cracker described above, we would have the \(\ell\) digits of the key and thus the plaintext.
To make things easier, suppose we take all of Hamlet and encrypt it with Vigenère using the keyword hippopotomonstrosesquipedaliophobia, corresponding to numerical key \[\begin{aligned} k=(7,8,15,15,14,15,14,19,14,12,14,13,18,19,17,14,\\ 18,4,18,16,20,8,15,4,3,0,11,8,14,15,7,14,1,8,0)\end{aligned}\] For example, the part of the ciphertext corresponding to the quote used above in Caesar cracking would be
hdxajnioomjvdtfvstrqitmfozlxjj
kcmiosgpenjjbgxmcmtfzltmaudofpmwg
odsntxuuhwjywmrjpnieosoqlfbpjoqyyljia
cmbdaozawminabtdhrtyndlncugkflswh
vjrwgdwddoeicznymcyl
If Eve was hoping this was only Caesar-encrypted, so the Vigenère key length was \(ℓ = 1\), she would have the following letter frequencies:
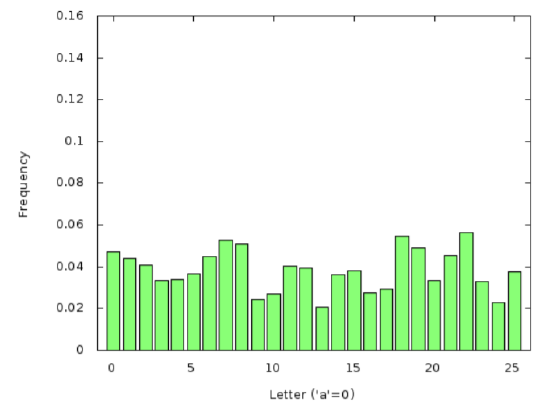
hippopotomonstrosesquipedaliophobia (Copyright; author via source)Notice that compared to Figure 4.3.2, the values show much less variation – in fact, there are no zero values and no values which are much larger than all others. The reason is that this distribution is the average of \(16\) different shifts, coming from the \(16\) different letters in the keywordhippopotomonstrosesquipedaliophobiaof the standard English distribution Figure 4.3.1. This averaging smooths out all of the characteristic shape of the distribution useful in identifying when its decrypting shift is correct.
Nevertheless, the Caesar cracker will give some key value for each one of the choices Eve makes for a possible value of \(\ell\) – there will always be a value of the shift for each letter which minimizes the square error. The minimum will not be very small, though, because the frequency distribution for the letters chosen as all locations in the ciphertext congruent to \(k\pmod{\ell}\) for any \(k\in\NN\) and \(k\le\ell\), where \(\ell\) is less than the true key size, will be quite flat and therefore far away (in the square error distance) from the distribution of standard English.
For example, with the encrypted Hamlet we have been examining, if Eve guesses that \(ℓ = 5\) and looks at every letter in a location congruent to \(1 (\text{mod } 5)\), the Caesar cracker will have the following graph of square error:
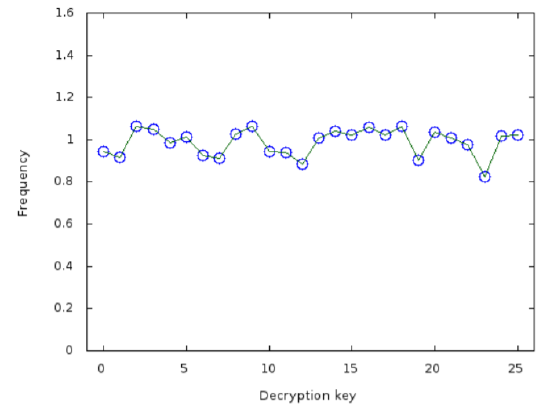
hippopotomonstrosesquipedaliophobia (Copyright; author via source)The minimum is clearly at a decryption key of \(23\), but it is not significantly less than other possibilities – and all the errors are around ten times higher than we saw in earlier such graphs such as Figure 4.3.3.
So here is the Vigenère cryptanalytic approach: Try all key lengths \(\ell\) up to some bound \(L\) (determined by how much computer time is available, and not so large that taking every \(\ell^{\text{th}}\) letter of the ciphertext results in too few letters to do reasonable frequency analysis). For each of the \(\ell\) substrings consisting of every \(\ell^{\text{th}}\) letter starting at locations \(1,\dots,\ell\), apply the Caesar cracker. This will result in an optimal Vigenère key \(\vec{k}_\ell=(k_{\ell,1},\dots,k_{\ell,\ell})\) of length \(\ell\). Then for each such \(\vec{k}_\ell\) in the range \(1,\dots,L\), compute the square error distance \(d_\ell\) between the ciphertext decrypted with \(\vec{k}_\ell\) and the standard English letter distribution. Report \(\ell\) and \(\vec{k}_\ell\) as the Vigenère keylength and key if \(d_\ell\) is the smallest square error computed.
Exercise \(\PageIndex{1}\)
- Can you think of any Caesar ciphertexts which would have two decryptions that would both seem like valid English during an brute-force attack? If so, give precise examples, with decryption keys.
- Would it be harder or easier to do the previous exercise (Exercise 4.3.1(1)) for the Vigenère cipher? Give reasoning and examples.
- It seems like more encryption would be better, in terms of designing a secure cryptosystem – so how about encrypting a cleartext using one cryptosystem, then re-encrypting the resulting ciphertext to make a super-ciphertext?
- We have two cryptosystems so far with short keys (we also have the one-time pad, but it is already perfectly secure and has big keys, those pads, so we will not consider it): Caesar and Vigenère. Suppose I make a new cryptosystem which does some combination of Caesar and Vigenère encryptions, one after the other, all with different keys. Will this result in a substantially more secure cryptosystem? Why or why not?


