5.1: Sturm-Liouville problems
- Page ID
- 329
Boundary Value Problems
In Chapter 4 we have encountered several different eigenvalue problems such as:
\[ X''(x)+ \lambda X(x)=0 \nonumber \]
with different boundary conditions
\[\begin{array}{rrl} X(0) = 0 & ~~X(L) = 0 & ~~\text{(Dirichlet), or} \\ X'(0) = 0 & ~~X'(L) = 0 & ~~\text{(Neumann), or} \\ X'(0) = 0 & ~~X(L) = 0 & ~~\text{(Mixed), or} \\ X(0) = 0 & ~~X'(L) = 0 & ~~\text{(Mixed)}, \ldots \end{array} \nonumber \]
For example for the insulated wire, Dirichlet conditions correspond to applying a zero temperature at the ends, Neumann means insulating the ends, etc…. Other types of endpoint conditions also arise naturally, such as the Robin boundary conditions
\[hX(0)-X'(0)=0\quad hX(L)+X'(L)=0, \nonumber \]
for some constant \(h\). These conditions come up when the ends are immersed in some medium.
Boundary problems came up in the study of the heat equation \(u_t=ku_{xx}\) when we were trying to solve the equation by the method of separation of variables in Section 4.6. In the computation we encountered a certain eigenvalue problem and found the eigenfunctions \(X_n(x)\). We then found the eigenfunction decomposition of the initial temperature \(f(x)=u(x,0)\) in terms of the eigenfunctions
\[f(x)= \sum_{n=1}^{\infty}c_nX_n(x). \nonumber \]
Once we had this decomposition and found suitable \(T_n(t)\) such that \(T_n(0)=1\) and \(T_n(t)X(x)\) were solutions, the solution to the original problem including the initial condition could be written as
\[u(x,t)= \sum_{n=1}^{\infty}c_nT_n(t)X_n(x). \nonumber \]
We will try to solve more general problems using this method. First, we will study second order linear equations of the form
\[\label{eq:6} \frac{d}{dx}\left( p(x)\frac{dy}{dx} \right)-q(x)y+\lambda r(x)y=0. \]
Essentially any second order linear equation of the form \(a(x)y''+b(x)y'+c(x)y+\lambda d(x)y=0\) can be written as \(\eqref{eq:6}\) after multiplying by a proper factor.
Put the following equation into the form \(\eqref{eq:6}\):
\[x^2y''+xy'+(\lambda x^2-n^2)y=0. \nonumber \]
Multiply both sides by \( \frac{1}{x}\) to obtain
\[\begin{align}\begin{aligned} \frac{1}{x}(x^2y''+xy'+(\lambda x^2-n^2)y) &=xy''+y'+ \left( \lambda x -\frac{n^2}{x}\right)y &= \frac{d}{dx}\left( x \frac{dy}{dx} \right)-\frac{n^2}{x}y+\lambda xy=0.\end{aligned}\end{align} \nonumber \]
The Bessel equation turns up for example in the solution of the two-dimensional wave equation. If you want to see how one solves the equation, you can look at subsection 7.3.3.
The so-called Sturm-Liouville problem\(^{1}\) is to seek nontrivial solutions to
\[\begin{align}\begin{aligned} \frac{d}{dx}\left( p(x)\frac{dy}{dx} \right)-q(x)y+\lambda r(x)y & =0,~~~~~a<x<b, \\ \alpha_1y(a)-\alpha_2y'(a) &=0, \\ \beta_1y(b)+\beta_2y'(b) &=0.\end{aligned}\end{align} \nonumber \]
In particular, we seek \(\lambda\)s that allow for nontrivial solutions. The \(\lambda\)s that admit nontrivial solutions are called the eigenvalues and the corresponding nontrivial solutions are called eigenfunctions. The constants \(\alpha_1\) and \(\alpha_2\) should not be both zero, same for \(\beta_1\) and \(\beta_2\).
Suppose \(p(x),\: p'(x),\: q(x)\) and \(r(x)\) are continuous on \([a,b]\) and suppose \(p(x)>0\) and \(r(x)>0\) for all \(x\) in \([a,b]\). Then the Sturm-Liouville problem (5.1.8) has an increasing sequence of eigenvalues
\[\lambda_1<\lambda_2<\lambda_3< \cdots \nonumber \]
such that
\[\lim_{n \rightarrow \infty} \lambda_n= +\infty \nonumber \]
and such that to each \(\lambda_n\) there is (up to a constant multiple) a single eigenfunction \(y_n(x)\).
Moreover, if \(q(x) \geq 0\) and \(\alpha_1, \alpha_2,\beta_1, \beta_2 \geq 0\), then \(\lambda_n \geq 0\) for all \(n\).
Problems satisfying the hypothesis of the theorem (including the "Moreover") are called regular Sturm-Liouville problems, and we will only consider such problems here. That is, a regular problem is one where \(p(x),\: p'(x),\: q(x)\) and \(r(x)\) are continuous, \(p(x)>0\), \(r(x)>0\), \(q(x) \geq 0\), and \(\alpha_1, \alpha_2,\beta_1, \beta_2 \geq 0\). Note: Be careful about the signs. Also be careful about the inequalities for \(r\) and \(p\), they must be strict for all \(x\) in the interval \([a,b]\), including the endpoints!
When zero is an eigenvalue, we usually start labeling the eigenvalues at \(0\) rather than at \(1\) for convenience. That is we label the eigenvalues \(\lambda_{0} <\lambda_{1} <\lambda_{2} <\cdots\).
The problem \(y''+ \lambda y,\: 0<x<L,\: y(0)=0\), and \(y(L)=0\) is a regular Sturm-Liouville problem: \(p(x)=1,\: q(x)=0,\: r(x)=1\), and we have \(p(x)1>0\) and \(r(x)1>0\). We also have \(a=0\), \(b=L\), \(\alpha_{1}=\beta_{1}=1\), \(\alpha_{2}=\beta_{2}=0\). The eigenvalues are \(\lambda_n=\frac{n^2 \pi^2}{L^2}\) and eigenfunctions are \(y_n(x)=\sin(\frac{n \pi}{L}x)\). All eigenvalues are nonnegative as predicted by the theorem.
Find eigenvalues and eigenfunctions for
\[y''+\lambda y=0,~~~~~y'(0)=0,~~~~~y'(1)=0. \nonumber \]
Identify the \(p,\: q,\: r,\: \alpha_j,\: \beta_j\). Can you use the theorem to make the search for eigenvalues easier? (Hint: Consider the condition \(-y'(0)=0\))
Find eigenvalues and eigenfunctions of the problem
\[\begin{align}\begin{aligned} y''+\lambda y &=0, & 0<x<1, \\ hy(0)-y'(0) & =0, & y'(1)=0, &\quad h>0.\end{aligned}\end{align} \nonumber \]
These equations give a regular Sturm-Liouville problem.
Identify \(p,\: q,\: r,\: \alpha_j,\: \beta_j\) in the example above.
First note that \(\lambda \geq 0\) by Theorem \(\PageIndex{1}\). Therefore, the general solution (without boundary conditions) is
\[\begin{align}\begin{aligned} & y(x) = A \cos ( \sqrt{\lambda}\, x) + B \sin ( \sqrt{\lambda}\, x) & & \qquad \text{if } \; \lambda > 0 , \\ & y(x) = A x + B & & \qquad \text{if } \; \lambda = 0 . \end{aligned}\end{align} \nonumber \]
Let us see if \(\lambda=0\) is an eigenvalue: We must satisfy \(0=hB-A\) and \(A=0\), hence \(B=0\) (as \(h>0\)), therefore, \(0\) is not an eigenvalue (no nonzero solution, so no eigenfunction).
Now let us try \(h>0\). We plug in the boundary conditions.
\[\begin{align}\begin{aligned} 0 &=hA- \sqrt{\lambda}B, \\ 0 &=-A\sqrt{\lambda}\sin(\sqrt{\lambda})+B\sqrt{\lambda}\cos(\sqrt{\lambda}).\end{aligned}\end{align} \nonumber \]
If \(A=0\), then \(B=0\) and vice-versa, hence both are nonzero. So \(B=\frac{hA}{\sqrt{\lambda}}\), and \(0=-A \sqrt{\lambda}\sin(\sqrt{\lambda})+\frac{hA}{\sqrt{\lambda}}\sqrt{\lambda}\cos(\sqrt{\lambda})\). As \(A \neq 0\) we get
\[0=- \sqrt{\lambda}\sin(\sqrt{\lambda})+h\cos(\sqrt{\lambda}), \nonumber \]
or
\[\frac{h}{\sqrt{\lambda}}= \tan \sqrt{\lambda}. \nonumber \]
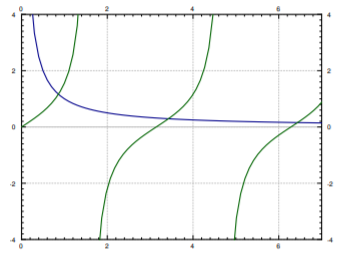
Now use a computer to find \(\lambda_n\). There are tables available, though using a computer or a graphing calculator is far more convenient nowadays. Easiest method is to plot the functions \(\frac{h}{x}\) and \(\tan(x)\) and see for which they intersect. There is an infinite number of intersections. Denote the first intersection by \(\sqrt{\lambda_1}\) the first intersection, by \(\sqrt{\lambda_2}\) the second intersection, etc…. For example, when \(h=1\), we get that \(\sqrt{\lambda_1}\approx 0.86,\: \sqrt{\lambda_2}\approx 3.43, ...\). That is \(\lambda_1 \approx 0.74,\: \lambda_2 \approx 11.73,... \), …. A plot for \(h=1\) is given in Figure \(\PageIndex{1}\). The appropriate eigenfunction (let \(A=1\) for convenience, then \(B= \frac{h}{\sqrt{\lambda}}\)) is
\[y_n(x)=\cos(\sqrt{\lambda_n}x)+\frac{h}{\sqrt{\lambda_n}}\sin(\sqrt{\lambda_n}x). \nonumber \]
When \(h=1\) we get (approximately)
\[y_1(x) \approx \cos(0.86x)+ \frac{1}{0.86} \sin(0.86x),\quad y_2(x) \approx \cos(3.43x)+ \frac{1}{3.43} \sin(3.43x),\quad .... \nonumber \]
Orthogonality
We have seen the notion of orthogonality before. For example, we have shown that \(\sin(nx)\) are orthogonal for distinct \(n\) on \([0, \pi]\). For general Sturm-Liouville problems we will need a more general setup. Let \(r(x)\) be a weight function (any function, though generally we will assume it is positive) on \([a, b]\). Two functions \(f(x)\), \(g(x)\) are said to be orthogonal with respect to the weight function \(r(x)\) when
\[\int_a^bf(x)g(x)r(x)dx=0. \nonumber \]
In this setting, we define the inner product as
\[ \langle f,g \rangle \overset{\rm{def}}= \int_a^bf(x)g(x)r(x)dx, \nonumber \]
and then say \(f\) and \(g\) are orthogonal whenever \(\langle f,g \rangle=0\). The results and concepts are again analogous to finite dimensional linear algebra.
The idea of the given inner product is that those \(x\) where \(r(x)\) is greater have more weight. Nontrivial (nonconstant) \(r(x)\) arise naturally, for example from a change of variables. Hence, you could think of a change of variables such that \(d \xi =r(x)dx\).
Eigenfunctions of a regular Sturm–Liouville problem satisfy an orthogonality property, just like the eigenfunctions in Section 4.1. Its proof is very similar to the analogous Theorem 4.1.1.
Suppose we have a regular Sturm-Liouville problem
\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=0, \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0.\end{aligned}\end{align} \nonumber \]
Let \(y_j\) and \(y_k\) be two distinct eigenfunctions for two distinct eigenvalues \(\lambda_j\) and \(\lambda_k\). Then
\[\int_a^by_j(x)y_k(x)r(x)dx=0, \nonumber \]
that is, \(y_j\) and \(y_k\) are orthogonal with respect to the weight function \(r\).
Fredholm Alternative
We also have the Fredholm alternative theorem we talked about before (Theorem 4.1.2) for all regular Sturm-Liouville problems. We state it here for completeness.
Fredholm Alternative
Suppose that we have a regular Sturm-Liouville problem. Then either
\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=0, \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0,\end{aligned}\end{align} \nonumber \]
has a nonzero solution, or
\[\begin{align}\begin{aligned} \frac{d}{dx} \left( p(x) \frac{dy}{dx} \right) -q(x)y+\lambda r(x)y &=f(x), \\ \alpha_1y(a)- \alpha_2y'(a) &=0, \\ \beta_1y(b)+ \beta_2y'(b) &=0,\end{aligned}\end{align} \nonumber \]
has a unique solution for any \(f(x)\) continuous on \([a,b]\).
This theorem is used in much the same way as we did before in Section 4.4. It is used when solving more general nonhomogeneous boundary value problems. The theorem does not help us solve the problem, but it tells us when a unique solution exists, so that we know when to spend time looking for it. To solve the problem we decompose \(f(x)\) and \(y(x)\) in terms of the eigenfunctions of the homogeneous problem, and then solve for the coefficients of the series for \(y(x)\).
Eigenfunction Series
What we want to do with the eigenfunctions once we have them is to compute the eigenfunction decomposition of an arbitrary function \(f(x)\). That is, we wish to write
\[\label{eq:26} f(x)= \sum_{n=1}^{\infty}c_ny_n(x), \]
where \(y_n(x)\) the eigenfunctions. We wish to find out if we can represent any function \(f(x)\) in this way, and if so, we wish to calculate (and of course we would want to know if the sum converges). OK, so imagine we could write \(f(x)\) as \(\eqref{eq:26}\). We will assume convergence and the ability to integrate the series term by term. Because of orthogonality we have
\[\begin{align}\begin{aligned} \langle f,y_m \rangle &= \int_a^bf(x)y_m(x)r(x)dx \\ &= \sum_{n=1}^{\infty}c_n \int_a^by_n(x)y_m(x)r(x)dx \\ &=c_m \int_a^by_m(x)y_m(x)r(x)dx= c_m \langle y_m,y_m \rangle .\end{aligned}\end{align} \nonumber \]
Hence,
\[\label{eq:28} c_m= \frac{\langle f,y_m \rangle}{\langle y_m,y_m \rangle}= \frac{\int_a^bf(x)y_m(x)r(x)dx}{\int_a^b(y_m(x))^2r(x)dx}. \]
Note that \(y_m\) are known up to a constant multiple, so we could have picked a scalar multiple of an eigenfunction such that \(\langle y_m,y_m \rangle=1\) (if we had an arbitrary eigenfunction \(\tilde{y}_m\), divide it by \(\sqrt{\langle \tilde{y}_m,\tilde{y}_m \rangle}\)). When \(\langle y_m,y_m \rangle=1\) we have the simpler form \(c_m=\langle f,y_m \rangle\) as we did for the Fourier series. The following theorem holds more generally, but the statement given is enough for our purposes.
Suppose \(f\) is a piecewise smooth continuous function on . If \(y_1,y_2, \ldots\) are the eigenfunctions of a regular Sturm-Liouville problem, then there exist real constants \(c_1,c_2, \ldots\) given by \(\eqref{eq:28}\) such that \(\eqref{eq:26}\) converges and holds for \(a<x<b\).
Take the simple Sturm-Liouville problem
\[\begin{align}\begin{aligned} & y'' + \lambda y = 0, \quad 0 < x < \frac{\pi}{2} , \\ & y(0) =0, \quad y'(\frac{\pi}{2}) = 0 .\end{aligned}\end{align} \nonumber \]
The above is a regular problem and furthermore we know by Theorem \(\PageIndex{1}\) that \(\lambda \geq 0\).
Suppose \(\lambda = 0\), then the general solution is \(y(x)Ax+B\), we plug in the initial conditions to get \(0=y(0)=B\), and \(0=y'(\pi/2)=A\), hence \(\lambda=0\) is not an eigenvalue. The general solution, therefore, is
\[y(x)=A\cos(\sqrt{\lambda}x)+B\sin(\sqrt{\lambda}x). \nonumber \]
Plugging in the boundary conditions we get \(0=y(0)=A\) and \(0=y'(\pi/2)=\sqrt{\lambda}B\cos(\sqrt{\lambda}\frac{\pi}{2})\). \(B\) cannot be zero and hence \(\cos(\sqrt{\lambda}\frac{\pi}{2}=0)\). This means that \(\sqrt{\lambda}\frac{\pi}{2}\) must be an odd integral multiple of \(\frac{\pi}{2}\), i.e. \((2n-1)\frac{\pi}{2}=\sqrt{\lambda_n}\frac{\pi}{2}\). Hence
\[\lambda_n=(2n-1)^2. \nonumber \]
We can take \(B=1\). Hence our eigenfunctions are
\[ y_n(x)= \sin((2n-1)x). \nonumber \]
Finally we compute
\[ \int_0^{\frac{\pi}{2}}(\sin((2n-1)x))^2dx=\frac{\pi}{4}. \nonumber \]
So any piecewise smooth function on \([0, \pi/2]\) can be written as
\[f(x)=\sum_{n=1}^{\infty}c_n\sin((2n-1)x), \nonumber \]
where
\[c_n= \frac{\langle f,y_n \rangle}{\langle y_n,y_n \rangle}= \frac{\int_0^{\frac{\pi}{2}}\sin((2n-1)x)dx}{\int_0^{\frac{\pi}{2}}(\sin((2n-1)x))^2dx}= \frac{4}{\pi} \int f(x)_{0}^{\frac{\pi}{2}}\sin((2n-1)x)dx. \nonumber \]
Note that the series converges to an odd \(2\pi\)-periodic (not \(\pi\)-periodic!) extension of \(f(x)\).
In the above example, the function is defined on \(0<x< \pi/2\), yet the series with respect to the eigenfunctions \(\sin ((2n-1)x)\) converges to an odd \(2\pi\)-periodic extension of \(f(x)\). Find out how is the extension defined for \(\pi/2 <x< \pi\).
Let us compute an example. Consider \(f(x) = x\) for \(0 < x < \frac{\pi}{2}\). Some calculus later we find \[c_n = \frac{4}{\pi} \int_0^{\frac{\pi}{2}} f(x) \,\sin \bigl( (2n-1)x \bigr) \, dx = \frac{4{(-1)}^{n+1}}{\pi {(2n-1)}^2} , \nonumber \] and so for \(x\) in \([0,\frac{\pi}{2}]\), \[f(x) = \sum_{n=1}^\infty \frac{4{(-1)}^{n+1}}{\pi {(2n-1)}^2} \sin \bigl( (2n-1)x \bigr) . \nonumber \]
This is different from the \(\pi\)-periodic regular sine series which can be computed to be
\[f(x)=\sum\limits_{n=1}^\infty \frac{(-1)^{n+1}}{n}\sin (2nx). \nonumber \]
Both sums converge are equal to \(f(x)\) for \(0 < x < \frac{\pi}{2}\), but the eigenfunctions involved come from different eigenvalue problems.
Footnotes
[1] Named after the French mathematicians Jacques Charles François Sturm (1803–1855) and Joseph Liouville (1809–1882).


