4.4: Autonomous Second Order Equations
- Page ID
- 9414
A second order differential equation that can be written as
\[\label{eq:4.4.1} y''=F(y,y')\]
where \(F\) is independent of \(t\), is said to be autonomous. An autonomous second order equation can be converted into a first order equation relating \(v=y'\) and \(y\). If we let \(v=y'\), Equation \ref{eq:4.4.1} becomes
\[\label{eq:4.4.2} v'=F(y,v).\]
Since
\[\label{eq:4.4.3} v'={dv\over dt}={dv\over dy}{dy\over dt}=v{dv\over dy},\]
Equation \ref{eq:4.4.2} can be rewritten as
\[\label{eq:4.4.4} v{dv\over dy}=F(y,v).\]
The integral curves of Equation \ref{eq:4.4.4} can be plotted in the \((y,v)\) plane, which is called the Poincaré phase plane of Equation \ref{eq:4.4.1}. If \(y\) is a solution of Equation \ref{eq:4.4.1} then \(y=y(t), v=y'(t)\) is a parametric equation for an integral curve of Equation \ref{eq:4.4.4}. we will call these integral curves trajectories of Equation \ref{eq:4.4.1}, and we will call Equation \ref{eq:4.4.4} the phase plane equivalent of Equation \ref{eq:4.4.1}.
In this section we will consider autonomous equations that can be written as
\[\label{eq:4.4.5} y''+q(y,y')y'+p(y)=0.\]
Equations of this form often arise in applications of Newton’s second law of motion. For example, suppose \(y\) is the displacement of a moving object with mass \(m\). It’s reasonable to think of two types of time-independent forces acting on the object. One type - such as gravity - depends only on position. We could write such a force as \(-mp(y)\). The second type - such as atmospheric resistance or friction - may depend on position and velocity. (Forces that depend on velocity are called damping forces.) We write this force as \(-mq(y,y')y'\), where \(q(y,y')\) is usually a positive function and we’ve put the factor \(y'\) outside to make it explicit that the force is in the direction opposing the motion. In this case Newton’s, second law of motion leads to Equation \ref{eq:4.4.5}.
The phase plane equivalent of Equation \ref{eq:4.4.5} is
\[\label{eq:4.4.6} v{dv\over dy}+q(y,v)v+p(y)=0.\]
Some statements that we will be making about the properties of Equation \ref{eq:4.4.5} and Equation \ref{eq:4.4.6} are intuitively reasonable, but difficult to prove. Therefore our presentation in this section will be informal: we will just say things without proof, all of which are true if we assume that \(p=p(y)\) is continuously differentiable for all \(y\) and \(q=q(y,v)\) is continuously differentiable for all \((y,v)\). We begin with the following statements:
- Statement 1: If \(y_0\) and \(v_0\) are arbitrary real numbers then Equation \(\ref{eq:4.4.5}\) has a unique solution on \((-\infty,\infty)\) such that \(y(0)=y_0\) and \(y'(0)=v_0\).
- Statement 2: If \(y=y(t)\) is a solution of Equation \(\ref{eq:4.4.5}\) and \(\tau\) is any constant then \(y_1=y(t-\tau)\) is also a solution of Equation \(\ref{eq:4.4.5}\), and \(y\) and \(y_1\) have the same trajectory.
- Statement 3: If two solutions \(y\) and \(y_1\) of Equation \(\ref{eq:4.4.5}\) have the same trajectory then \(y_1(t)=y(t-\tau)\) for some constant \(\tau\).
- Statement 4: Distinct trajectories of Equation \(\ref{eq:4.4.5}\) cannot intersect; that is, if two trajectories of Equation \(\ref{eq:4.4.5}\) intersect, they are identical.
- Statement 5: If the trajectory of a solution of Equation \ref{eq:4.4.5} is a closed curve then \((y(t),v(t))\) traverses the trajectory in a finite time \(T\), and the solution is periodic with period \(T\); that is, \(y(t+T)=y(t)\) for all \(t\) in \((-\infty,\infty)\).
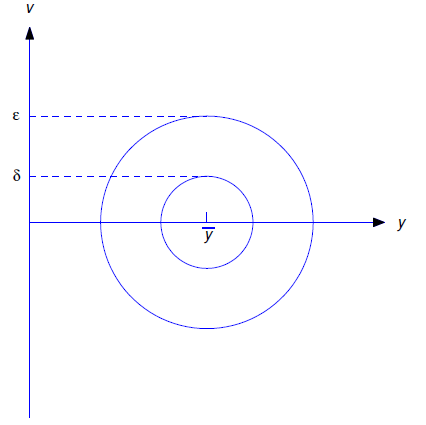
If \(\overline y\) is a constant such that \(p(\overline y)=0\) then \(y\equiv\overline y\) is a constant solution of Equation \ref{eq:4.4.5}. We say that \(\overline y\) is an equilibrium of Equation \ref{eq:4.4.5} and \((\overline y,0)\) is a critical point of the phase plane equivalent equation Equation \ref{eq:4.4.6}. We say that the equilibrium and the critical point are stable if, for any given \(\epsilon>0\) no matter how small, there’s a \(\delta>0\), sufficiently small, such that if
\[\sqrt{(y_0-\overline y)^2+v_0^2}<\delta \nonumber\]
then the solution of the initial value problem
\[y''+q(y,y')y'+p(y)=0,\quad y(0)=y_0,\quad y'(0)=v_0 \nonumber\]
satisfies the inequality
\[\sqrt{(y(t)-\overline y)^2+(v(t))^2}<\epsilon \nonumber\]
for all \(t>0\). Figure 4.4.1 illustrates the geometrical interpretation of this definition in the Poincaré phase plane: if \((y_0,v_0)\) is in the smaller shaded circle (with radius \(\delta\)), then \((y(t),v(t))\) must be in in the larger circle (with radius \(\epsilon\)) for all \(t>0\).
If an equilibrium and the associated critical point are not stable, we say they are unstable. To see if you really understand what stable means, try to give a direct definition of unstable (Exercise 4.4.22). we will illustrate both definitions in the following examples.
The Undamped Case
We will begin with the case where \(q\equiv0\), so Equation \ref{eq:4.4.5} reduces to
\[\label{eq:4.4.7} y''+p(y)=0.\]
We say that this equation - as well as any physical situation that it may model - is undamped. The phase plane equivalent of Equation \ref{eq:4.4.7} is the separable equation
\[v{dv\over dy}+p(y)=0. \nonumber \]
Integrating this yields
\[\label{eq:4.4.8} {v^2\over2}+P(y)=c,\]
where \(c\) is a constant of integration and \(\displaystyle P(y)=\int p(y)\,dy\) is an antiderivative of \(p\).
If Equation \ref{eq:4.4.7} is the equation of motion of an object of mass \(m\), then \(mv^2/2\) is the kinetic energy and \(mP(y)\) is the potential energy of the object; thus, Equation \ref{eq:4.4.8} says that the total energy of the object remains constant, or is conserved. In particular, if a trajectory passes through a given point \((y_0,v_0)\) then
\[c={v_0^2\over2}+P(y_0). \nonumber\]
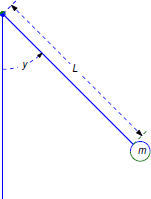
Consider an object with mass \(m\) suspended from a spring and moving vertically. Let \(y\) be the displacement of the object from the position it occupies when suspended at rest from the spring (Figure 4.4.2 ).

Assume that if the length of the spring is changed by an amount \(\Delta L\) (positive or negative), then the spring exerts an opposing force with magnitude \(k|\Delta L|\), where k is a positive constant. In Section 6.1, it will be shown that if the mass of the spring is negligible compared to \(m\) and no other forces act on the object then Newton’s second law of motion implies that
\[\label{eq:4.4.9} my''=-ky,\]
which can be written in the form Equation \ref{eq:4.4.7} with \(p(y)=ky/m\). This equation can be solved easily by a method that we will study in Section 5.2, but that method isn’t available here. Instead, we will consider the phase plane equivalent of Equation \ref{eq:4.4.9}.
From Equation \ref{eq:4.4.3}, we can rewrite Equation \ref{eq:4.4.9} as the separable equation
\[mv{dv\over dy}=-ky. \nonumber\]
Integrating this yields
\[{mv^2\over2}=-{ky^2\over2}+c, \nonumber\]
which implies that
\[\label{eq:4.4.10} mv^2+ky^2=\rho\]
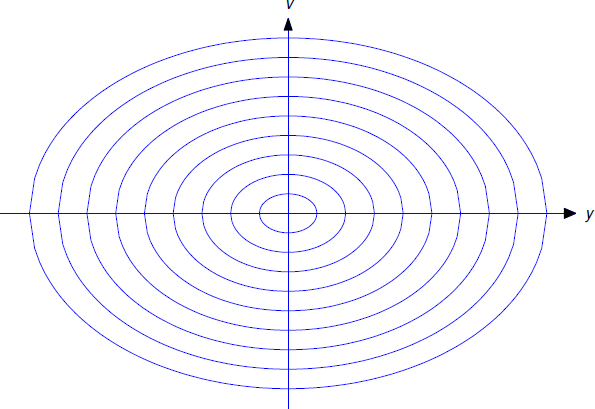
(\(\rho=2c\)). This defines an ellipse in the Poincaré phase plane (Figure 4.4.3 ).
We can identify \(\rho\) by setting \(t=0\) in Equation \ref{eq:4.4.10}; thus, \(\rho=mv_0^2+ky_0^2\), where \(y_0=y(0)\) and \(v_0=v(0)\). To determine the maximum and minimum values of \(y\) we set \(v=0\) in Equation \ref{eq:4.4.10}; thus,
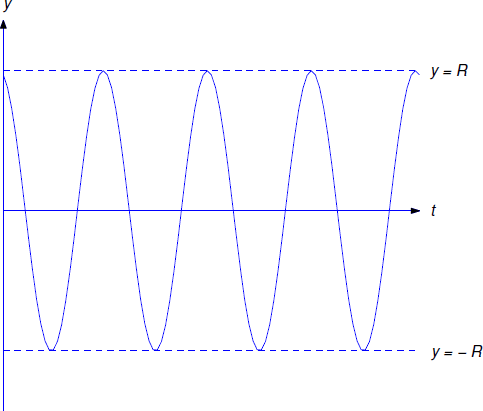
\[\label{eq:4.4.11} y_{\max}=R \quad \text{and} \quad y_{\min}=-R, \quad \text{with} R=\sqrt{\rho\over k}.\]
Equation \ref{eq:4.4.9} has exactly one equilibrium, \(\overline y=0\), and it is stable. You can see intuitively why this is so: if the object is displaced in either direction from equilibrium, the spring tries to bring it back.
In this case we can find \(y\) explicitly as a function of \(t\). (Don’t expect this to happen in more complicated problems!) If \(v>0\) on an interval \(I\), Equation \ref{eq:4.4.10} implies that
\[{dy\over dt}=v=\sqrt{\rho-ky^2\over m} \nonumber\]
on \(I\). This is equivalent to
\[\label{eq:4.4.12} {\sqrt k\over\sqrt{\rho-ky^2}}{dy\over dt}=\omega_0,\quad \text{where} \quad \omega_0=\sqrt{k\over m}.\]
Since
\[ \begin{align*} \int{\sqrt k\,dy\over\sqrt{\rho-ky^2}} &=\sin^{-1}\left(\sqrt{k\over\rho }y\right)+c \\[4pt] &=\sin^{-1}\left(y\over R\right)+c \end{align*}\]
(see Equation \ref{eq:4.4.11}), Equation \ref{eq:4.4.12} implies that that there’s a constant \(\phi\) such that
\[\sin^{-1}\left(y\over R\right)=\omega_0 t+\phi \nonumber\]
or
\[y=R\sin(\omega_0 t+\phi) \nonumber\]
for all \(t\) in \(I\). Although we obtained this function by assuming that \(v>0\), you can easily verify that \(y\) satisfies Equation \ref{eq:4.4.9} for all values of \(t\). Thus, the displacement varies periodically between \(-R\) and \(R\), with period \(T=2\pi/\omega_0\) (Figure 4.4.4 ). (If you’ve taken a course in elementary mechanics you may recognize this as simple harmonic motion.)
Now we consider the motion of a pendulum with mass \(m\), attached to the end of a weightless rod with length \(L\) that rotates on a frictionless axle (Figure 4.4.5 ). We assume that there’s no air resistance.
Let \(y\) be the angle measured from the rest position (vertically downward) of the pendulum, as shown in Figure 4.4.5 . Newton’s second law of motion says that the product of \(m\) and the tangential acceleration equals the tangential component of the gravitational force; therefore, from Figure 4.4.5 ,
\[mLy''=-mg\sin y, \nonumber\]
or
\[\label{eq:4.4.13} y''=-{g\over L} \sin y.\]
Since \(\sin n\pi=0\) if \(n\) is any integer, Equation \ref{eq:4.4.13} has infinitely many equilibria \(\overline y_n=n\pi\). If \(n\) is even, the mass is directly below the axle (Figure \(\PageIndex{6a}\)) and gravity opposes any deviation from the equilibrium.
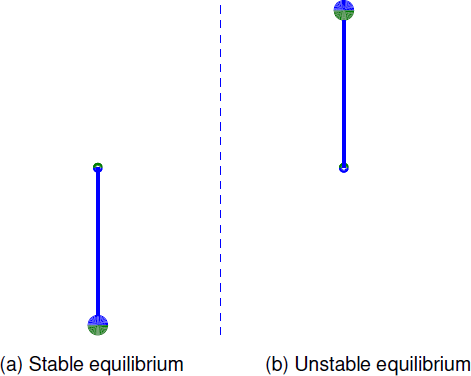
However, if \(n\) is odd, the mass is directly above the axle (Figure \(\PageIndex{6b}\)) and gravity increases any deviation from the equilibrium. Therefore we conclude on physical grounds that \(\overline y_{2m}=2m\pi\) is stable and \(\overline y_{2m+1}=(2m+1)\pi\) is unstable.
The phase plane equivalent of Equation \ref{eq:4.4.13} is
\[v{dv\over dy}=-{g\over L}\sin y, \nonumber\]
where \(v=y'\) is the angular velocity of the pendulum. Integrating this yields
\[\label{eq:4.4.14} {v^2\over2}={g\over L}\cos y+c.\]
If \(v=v_0\) when \(y=0\), then
\[c={v_0^2\over2}-{g\over L}, \nonumber\]
so Equation \ref{eq:4.4.14} becomes
\[ \begin{align*} {v^2\over2} &={v_0^2\over2}-{g\over L}(1-\cos y) \\[4pt] &={v_0^2\over2}-{2g\over L}\sin^2{y\over2}, \end{align*}\]
which is equivalent to
\[\label{eq:4.4.15} v^2=v_0^2-v_c^2\sin^2{y\over2},\]
where
\[v_c=2\sqrt{g\over L}. \nonumber\]
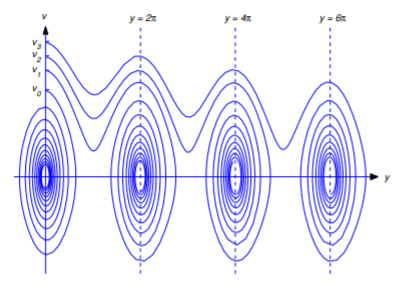
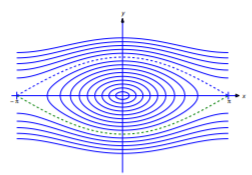
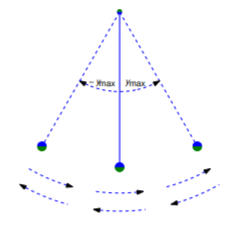
The curves defined by Equation \ref{eq:4.4.15} are the trajectories of Equation \ref{eq:4.4.13}. They are periodic with period \(2\pi\) in \(y\), which isn’t surprising, since if \(y=y(t)\) is a solution of Equation \ref{eq:4.4.13} then so is \(y_n=y(t)+2n\pi\) for any integer \(n\). Figure 4.4.7 shows trajectories over the interval \([-\pi,\pi]\). From Equation \ref{eq:4.4.15}, you can see that if \(|v_0|>v_c\) then \(v\) is nonzero for all \(t\), which means that the object whirls in the same direction forever, as in Figure 4.4.8 . The trajectories associated with this whirling motion are above the upper dashed curve and below the lower dashed curve in Figure 4.4.7 . You can also see from Equation \ref{eq:4.4.15} that if \(0<|v_{0}|<v_{c}\), then \(v=0\) when \(y=\pm y_{max}\), where
\[y_{\max}=2\sin^{-1}(|v_0|/v_c). \nonumber\]
In this case the pendulum oscillates periodically between \(-y_{\max}\) and \(y_{\max}\), as shown in Figure 4.4.9 . The trajectories associated with this kind of motion are the ovals between the dashed curves in Figure 4.4.7 . It can be shown (see Exercise 4.4.21 for a partial proof) that the period of the oscillation is
\[\label{eq:4.4.16} T=8\int_0^{\pi/2}{d\theta\over\sqrt{v_c^2-v_0^2\sin^2\theta}}.\]
Although this integral cannot be evaluated in terms of familiar elementary functions, you can see that it is finite if \(|v_0|<v_c\).>
The dashed curves in Figure 4.4.7 contain four trajectories. The critical points \((\pi,0)\) and \((-\pi,0)\) are the trajectories of the unstable equilibrium solutions \(\overline y=\pm\pi\). The upper dashed curve connecting (but not including) them is obtained from initial conditions of the form \(y(t_0)=0,\ v(t_0)=v_c\). If \(y\) is any solution with this trajectory then
\[\displaystyle \lim_{t\to\infty}y(t)=\pi \quad \text{and} \quad \displaystyle \lim_{t\to-\infty}y(t)=-\pi. \nonumber\]
The lower dashed curve connecting (but not including) them is obtained from initial conditions of the form \(y(t_0)=0,\ v(t_0)=-v_c\). If \(y\) is any solution with this trajectory then
\[\displaystyle \lim_{t\to\infty}y(t)=-\pi\quad \text{and} \quad \displaystyle \lim_{t\to-\infty}y(t)=\pi. \nonumber\]
Consistent with this, the integral Equation \ref{eq:4.4.16} diverges to \(\infty\) if \(v_0=\pm v_c\). (Exercise 4.4.21).
Since the dashed curves separate trajectories of whirling solutions from trajectories of oscillating solutions, each of these curves is called a separatrix.
In general, if Equation \ref{eq:4.4.7} has both stable and unstable equilibria then the separatrices are the curves given by Equation \ref{eq:4.4.8} that pass through unstable critical points. Thus, if \((\overline y,0)\) is an unstable critical point, then
\[\label{eq:4.4.17} {v^2\over 2}+P(y)=P(\overline y)\]
defines a separatrix passing through \((\overline y,0)\).
Stability and Instability Conditions for y'' + p(y) = 0
It can be shown (Exercise 4.4.23) that an equilibrium \(\overline y\) of an undamped equation
\[\label{eq:4.4.18} y''+p(y)=0\]
is stable if there’s an open interval \((a,b)\) containing \(\overline y\) such that
\[\label{eq:4.4.19} p(y)<0\text{ if }a<y<\overline{y}\text{ and } p(y)>0\text{ if }\overline{y}<y<b\]
If we regard \(p(y)\) as a force acting on a unit mass, Equation \ref{eq:4.4.19} means that the force resists all sufficiently small displacements from \(\overline y\).
We’ve already seen examples illustrating this principle. The equation Equation \ref{eq:4.4.9} for the undamped spring-mass system is of the form Equation \ref{eq:4.4.18} with \(p(y)=ky/m\), which has only the stable equilibrium \(\overline y=0\). In this case Equation \ref{eq:4.4.19} holds with \(a=-\infty\) and \(b=\infty\). The equation Equation \ref{eq:4.4.13} for the undamped pendulum is of the form Equation \ref{eq:4.4.18} with \(p(y)=(g/L)\sin y\). We’ve seen that \(\overline y=2m\pi\) is a stable equilibrium if \(m\) is an integer. In this case
\[p(y)=\sin y<0\text{ if } (2m-1)\pi <y<2m\pi \nonumber \]
and
\[p(y)>0\text{ if } 2m\pi <y<(2m+1)\pi \nonumber \]
It can also be shown (Exercise 4.4.24) that \(\overline y\) is unstable if there’s a \(b>\overline y\) such that
\[\label{eq:4.4.20} p(y)<0\text{ if } \overline{y}<y<b\]
or an \(a<\overline y\) such that
\[\label{eq:4.4.21} p(y)>0\text{ if } a<y<\overline{y}\]
If we regard \(p(y)\) as a force acting on a unit mass, Equation \ref{eq:4.4.20} means that the force tends to increase all sufficiently small positive displacements from \(\overline y\), while Equation \ref{eq:4.4.21} means that the force tends to increase the magnitude of all sufficiently small negative displacements from \(\overline y\).
The undamped pendulum also illustrates this principle. We’ve seen that \(\overline y=(2m+1)\pi\) is an unstable equilibrium if \(m\) is an integer. In this case
\[\sin y<0\text{ if }(2m+1)\pi <y<(2m+2)\pi \nonumber \]
so Equation \ref{eq:4.4.20} holds with \(b=(2m+2)\pi\), and
\[\sin y>0\text{ if }2m\pi <y<(2m+1)\pi \nonumber \]
so Equation \ref{eq:4.4.21} holds with \(a=2m\pi\).
The equation
\[\label{eq:4.4.22} y''+y(y-1)=0\]
is of the form Equation \ref{eq:4.4.18} with \(p(y)=y(y-1)\). Therefore \(\overline y=0\) and \(\overline y=1\) are the equilibria of Equation \ref{eq:4.4.22}. Since
\[\begin{aligned} y(y-1)&>0 &\text{if} &y<0 \text{ or }y>1 \\ &<0 &\text{if} &0<y<1 \end{aligned} \nonumber \]
\(\overline y=0\) is unstable and \(\overline y=1\) is stable.
The phase plane equivalent of Equation \ref{eq:4.4.22} is the separable equation
\[v{dv\over dy}+y(y-1)=0. \nonumber \]
Integrating yields
\[{v^2\over2}+{y^3\over3}-{y^2\over2}=C, \nonumber\]
which we rewrite as
\[\label{eq:4.4.23} v^2+{1\over3}y^2(2y-3)=c\]
after renaming the constant of integration. These are the trajectories of Equation \ref{eq:4.4.22}. If \(y\) is any solution of Equation \ref{eq:4.4.22}, the point \((y(t),v(t))\) moves along the trajectory of \(y\) in the direction of increasing \(y\) in the upper half plane (\(v=y'>0\)), or in the direction of decreasing \(y\) in the lower half plane (\(v=y'<0\)).
Figure 4.4.10 shows typical trajectories. The dashed curve through the critical point \((0,0)\), obtained by setting \(c=0\) in Equation \ref{eq:4.4.23}, separates the \(y\)-\(v\) plane into regions that contain different kinds of trajectories; again, we call this curve a separatrix. Trajectories in the region bounded by the closed loop (b) are closed curves, so solutions associated with them are periodic. Solutions associated with other trajectories are not periodic. If \(y\) is any such solution with trajectory not on the separatrix, then
\[\begin{array}{llrllr} \displaystyle \lim_{t\to\infty}y(t) &= -\infty, &\displaystyle \lim_{t\to-\infty}y(t) &= -\infty,\\ \displaystyle \lim_{t\to\infty}v(t) &= -\infty, &\displaystyle \lim_{t\to-\infty}v(t) &= \infty. \end{array} \nonumber \]
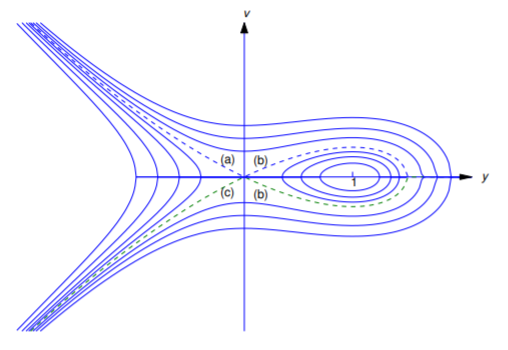
The separatrix contains four trajectories of Equation \ref{eq:4.4.22}. One is the point \((0,0)\), the trajectory of the equilibrium \(\overline y=0\). Since distinct trajectories cannot intersect, the segments of the separatrix marked (a), b, and (c)– which don’t include \((0,0)\) – are distinct trajectories, none of which can be traversed in finite time. Solutions with these trajectories have the following asymptotic behavior:
\[\begin{array}{llrllrl} \displaystyle \lim_{t\to\infty}y(t) &= 0, &\displaystyle \lim_{t\to-\infty}y(t) &= -\infty,\\ \displaystyle \lim_{t\to\infty}v(t) &= 0, &\displaystyle \lim_{t\to-\infty}v(t) &= \infty\phantom{,}& \text{(on (a))} \\ \displaystyle \lim_{t\to\infty}y(t) &= 0, &\displaystyle \lim_{t\to-\infty}y(t) &= 0,\\ \displaystyle \lim_{t\to\infty}v(t) &= 0, &\displaystyle \lim_{t\to-\infty}v(t) &= 0\phantom{,}& \text{(on (b))} \\ \displaystyle \lim_{t\to\infty}y(t) &= -\infty, &\displaystyle \lim_{t\to-\infty}y(t) &= 0,\\ \displaystyle \lim_{t\to\infty}v(t) &= -\infty, &\displaystyle \lim_{t\to-\infty}v(t) &= 0\phantom{,}& \text{(on (c))}. \end{array}. \nonumber \]
The Damped Case
The phase plane equivalent of the damped autonomous equation
\[\label{eq:4.4.24} y''+q(y,y')y'+p(y)=0\]
is
\[v{dv\over dy}+q(y,v)v+p(y)=0. \nonumber\]
This equation isn’t separable, so we cannot solve it for \(v\) in terms of \(y\), as we did in the undamped case, and conservation of energy doesn’t hold. (For example, energy expended in overcoming friction is lost.) However, we can study the qualitative behavior of its solutions by rewriting it as
\[\label{eq:4.4.25} {dv\over dy}=-q(y,v)-{p(y)\over v}\]
and considering the direction fields for this equation.
In the following examples we will also be showing computer generated trajectories of this equation, obtained by numerical methods. The exercises call for similar computations. The methods discussed in Chapter 3 are not suitable for this task, since \(p(y)/v\) in Equation \ref{eq:4.4.25} is undefined on the \(y\) axis of the Poincaré phase plane. Therefore we are forced to apply numerical methods briefly discussed in Section 10.1 to the system
\[\begin{aligned} y'&= v\\ v'&= -q(y,v)v-p(y),\end{aligned}\]
which is equivalent to Equation \ref{eq:4.4.24} in the sense defined in Section 10.1. Fortunately, most differential equation software packages enable you to do this painlessly.
In the text we will confine ourselves to the case where \(q\) is constant, so Equation \ref{eq:4.4.24} and Equation \ref{eq:4.4.25} reduce to
\[\label{eq:4.4.26} y''+cy'+p(y)=0\]
and
\[{dv\over dy}=-c-{p(y)\over v}. \nonumber\]
(we will consider more general equations in the exercises.) The constant \(c\) is called the damping constant. In situations where Equation \ref{eq:4.4.26} is the equation of motion of an object, \(c\) is positive; however, there are situations where \(c\) may be negative.
The Damped Spring-Mass System
Earlier we considered the spring - mass system under the assumption that the only forces acting on the object were gravity and the spring’s resistance to changes in its length. Now we will assume that some mechanism (for example, friction in the spring or atmospheric resistance) opposes the motion of the object with a force proportional to its velocity. In Section 6.1 it will be shown that in this case Newton’s second law of motion implies that
\[\label{eq:4.4.27} my''+cy'+ky=0,\]
where \(c>0\) is the damping constant. Again, this equation can be solved easily by a method that we will study in Section 5.2, but that method isn’t available here. Instead, we will consider its phase plane equivalent, which can be written in the form Equation \ref{eq:4.4.25} as
\[\label{eq:4.4.28} {dv\over dy}=-{c\over m}-{ky\over mv}.\]
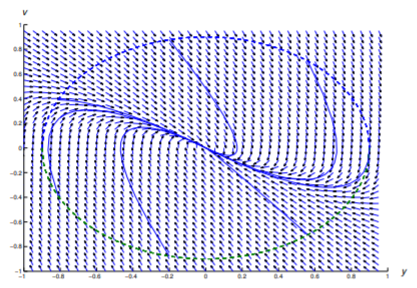
(A minor note: the \(c\) in Equation \ref{eq:4.4.26} actually corresponds to \(c/m\) in this equation.) Figure 4.4.11 shows a typical direction field for an equation of this form. Recalling that motion along a trajectory must be in the direction of increasing \(y\) in the upper half plane (\(v>0\)) and in the direction of decreasing \(y\) in the lower half plane (\(v<0\)), you can infer that all trajectories approach the origin in clockwise fashion. To confirm this, Figure 4.4.12 shows the same direction field with some trajectories filled in. All the trajectories shown there correspond to solutions of the initial value problem
\[my''+cy'+ky=0,\quad y(0)=y_0,\quad y'(0)=v_0, \nonumber\]
where
\[mv_0^2+ky_0^2=\rho\quad (\mbox{a positive constant}); \nonumber \]
thus, if there were no damping (\(c=0\)), all the solutions would have the same dashed elliptic trajectory, shown in Figure 4.4.14 .


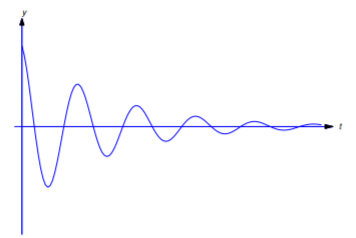
Solutions corresponding to the trajectories in Figure 4.4.12 cross the \(y\)-axis infinitely many times. The corresponding solutions are said to be oscillatory (Figure 4.4.13 ) It is shown in Section 6.2 that there’s a number \(c_1\) such that if \(0\leq c<c_{1}\) then all solutions of (4.4.27 ) are oscillatory, while if \(c\geq c_{1}\), no solutions of (4.4.27 ) have this property. (In fact, no solution not identically zero can have more than two zeros in this case.) Figure 4.4.14 shows a direction field and some integral curves for (4.4.28 ) in this case.
Now we return to the pendulum. If we assume that some mechanism (for example, friction in the axle or atmospheric resistance) opposes the motion of the pendulum with a force proportional to its angular velocity, Newton’s second law of motion implies that
\[\label{eq:4.4.29} mLy''=-cy'-mg\sin y,\]
where \(c>0\) is the damping constant. (Again, a minor note: the \(c\) in Equation \ref{eq:4.4.26} actually corresponds to \(c/mL\) in this equation.) To plot a direction field for Equation \ref{eq:4.4.29} we write its phase plane equivalent as
\[{dv\over dy}=-{c\over mL}-{g\over Lv}\sin y. \nonumber\]
Figure 4.4.15 shows trajectories of four solutions of Equation \ref{eq:4.4.29}, all satisfying \(y(0)=0\). For each \(m=0\), \(1\), \(2\), \(3\), imparting the initial velocity \(v(0)=v_m\) causes the pendulum to make \(m\) complete revolutions and then settle into decaying oscillation about the stable equilibrium \(\overline y=2m\pi\).