4.5: Applications to Curves
- Page ID
- 9415
We begin with two examples of families of curves generated by varying a parameter over a set of real numbers.
For each value of the parameter \(c\), the equation
\[\label{eq:4.5.1} y-cx^2=0\]
defines a curve in the \(xy\)-plane. If \(c \ne0\), the curve is a parabola through the origin, opening upward if \(c>0\) or downward if \(c<0\). If \(c=0\), the curve is the \(x\) axis (Figure 4.5.1 ).
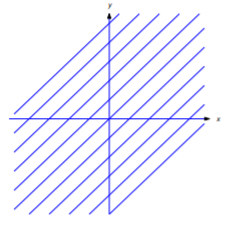
For each value of the parameter \(c\) the equation
\[\label{eq:4.5.2} y=x+c\]
defines a line with slope 1(Figure 4.5.2 ).
An equation that can be written in the form
\[\label{eq:4.5.3} H(x,y,c)=0\]
is said to define a one-parameter family of curves if\(,\) for each value of \(c\) in in some nonempty set of real numbers\(,\) the set of points \((x,y)\) that satisfy Equation \ref{eq:4.5.3} forms a curve in the \(xy\)-plane.
Equations Equation \ref{eq:4.5.1} and Equation \ref{eq:4.5.2} define one–parameter families of curves. (Although Equation \ref{eq:4.5.2} isn’t in the form Equation \ref{eq:4.5.3}, it can be written in this form as \(y-x-c=0\).)
If \(c>0\), the graph of the equation
\[\label{eq:4.5.4} x^2+y^2-c=0\]
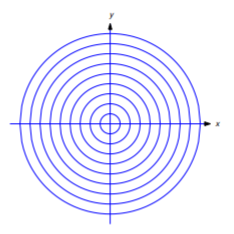
is a circle with center at \((0,0)\) and radius \(\sqrt{c}\). If \(c=0\), the graph is the single point \((0,0)\). (We don’t regard a single point as a curve.) If \(c<0\), the equation has no graph. Hence, Equation \ref{eq:4.5.4} defines a one–parameter family of curves for positive values of \(c\). This family consists of all circles centered at \((0,0)\) (Figure 4.5.3 ).
The equation
\[x^2+y^2+c^2=0 \nonumber\]
does not define a one-parameter family of curves, since no \((x,y)\) satisfies the equation if \(c\ne0\), and only the single point \((0,0)\) satisfies it if \(c=0\).
Recall from Section 1.2 that the graph of a solution of a differential equation is called an integral curve of the equation. Solving a first order differential equation usually produces a one–parameter family of integral curves of the equation. Here we are interested in the converse problem: given a one–parameter family of curves, is there a first order differential equation for which every member of the family is an integral curve. This suggests the next definition.
4.5.2 If every curve in a one-parameter family defined by the equation
\[\label{eq:4.5.5} H(x,y,c)=0\]
is an integral curve of the first order differential equation
\[\label{eq:4.5.6} F(x,y,y')=0,\]
then Equation \ref{eq:4.5.6} is said to be a differential equation for the family.
To find a differential equation for a one–parameter family we differentiate its defining equation Equation \ref{eq:4.5.5} implicitly with respect to \(x\), to obtain
\[\label{eq:4.5.7} H_x(x,y,c)+H_y(x,y,c)y'=0.\]
If this equation doesn’t, then it is a differential equation for the family. If it does contain \(c\), it may be possible to obtain a differential equation for the family by eliminating \(c\) between Equation \ref{eq:4.5.5} and Equation \ref{eq:4.5.7}.
Find a differential equation for the family of curves defined by
\[\label{eq:4.5.8} y=cx^2.\]
Solution
Differentiating Equation \ref{eq:4.5.8} with respect to \(x\) yields
\[y'=2cx. \nonumber\]
Therefore \(c=y'/2x\), and substituting this into Equation \ref{eq:4.5.8} yields
\[y={xy'\over2} \nonumber\]
as a differential equation for the family of curves defined by Equation \ref{eq:4.5.8}. The graph of any function of the form \(y=cx^2\) is an integral curve of this equation.
The next example shows that members of a given family of curves may be obtained by joining integral curves for more than one differential equation.
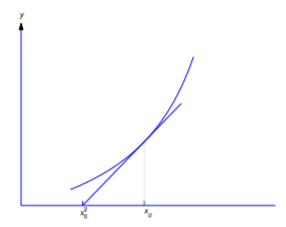
a. Try to find a differential equation for the family of lines tangent to the parabola \(y=x^2\).
b. Find two tangent lines to the parabola \(y=x^2\) that pass through \((2,3)\), and find the points of tangency.
Solution
a. The equation of the line through a given point \((x_0,y_0)\) with slope \(m\) is
\[\label{eq:4.5.9} y=y_0+m(x-x_0).\]
If \((x_0,y_0)\) is on the parabola, then \(y_0=x_0^2\) and the slope of the tangent line through (\(x_0,x_0^2)\) is \(m=2x_0\); hence, Equation \ref{eq:4.5.9} becomes
\[y=x_0^2+2x_0(x-x_0), \nonumber\]
or, equivalently,
\[\label{eq:4.5.10} y=-x_0^2+2x_0x.\]
Here \(x_0\) plays the role of the constant \(c\) in Definition 4.5.1 ; that is, varying \(x_0\) over \((-\infty,\infty)\) produces the family of tangent lines to the parabola \(y=x^2\).
Differentiating Equation \ref{eq:4.5.10} with respect to \(x\) yields \(y'=2x_0\).. We can express \(x_0\) in terms of \(x\) and \(y\) by rewriting Equation \ref{eq:4.5.10} as
\[x_0^2-2x_0x+y=0 \nonumber\]
and using the quadratic formula to obtain
\[\label{eq:4.5.11} x_0=x\pm\sqrt{x^2-y}.\]
We must choose the plus sign in Equation \ref{eq:4.5.11} if \(x<x_0\) and the minus sign if \(x>x_0\); thus,
\[x_0=\left(x+\sqrt{x^2-y}\right)\, \text{if} \, x<x_0. \nonumber\]
and
\[x_0=\left(x-\sqrt{x^2-y}\right)\, \text{if} \, x>x_0. \nonumber\]
Since \(y'=2x_0\), this implies that
\[\label{eq:4.5.12} y'=2\left(x+\sqrt{x^2-y}\right),\quad \text{if} \quad x<x_0\]
and
\[\label{eq:4.5.13} y'=2\left(x-\sqrt{x^2-y}\right),\quad \text{if} \quad x>x_0.\]
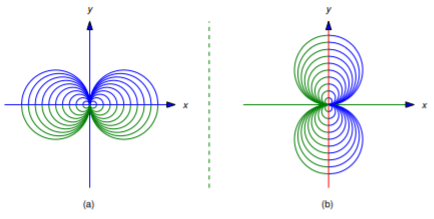
Neither Equation \ref{eq:4.5.12} nor Equation \ref{eq:4.5.13} is a differential equation for the family of tangent lines to the parabola \(y=x^2\). However, if each tangent line is regarded as consisting of two tangent half lines joined at the point of tangency, Equation \ref{eq:4.5.12} is a differential equation for the family of tangent half lines on which \(x\) is less than the abscissa of the point of tangency (Figure 4.5.4 a), while Equation \ref{eq:4.5.13} is a differential equation for the family of tangent half lines on which \(x\) is greater than this abscissa (Figure 4.5.4 (b)). The parabola \(y=x^2\) is also an integral curve of both Equation \ref{eq:4.5.12} and Equation \ref{eq:4.5.13}.
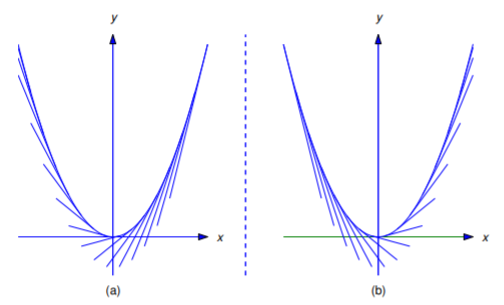
b. From Equation \ref{eq:4.5.10} the point \((x,y)=(2,3)\) is on the tangent line through \((x_0,x_0^2)\) if and only if
\[3=-x_0^2+4x_0, \nonumber\]
which is equivalent to
\[x_0^2-4x_0+3=(x_0-3)(x_0-1)=0. \nonumber\]
Letting \(x_0=3\) in Equation \ref{eq:4.5.10} shows that \((2,3)\) is on the line
\[y=-9+6x, \nonumber \]
which is tangent to the parabola at \((x_0,x_0^2)=(3,9)\), as shown in Figure 4.5.5
Letting \(x_0=1\) in Equation \ref{eq:4.5.10} shows that \((2,3)\) is on the line
\[y=-1+2x, \nonumber\]
which is tangent to the parabola at \((x_0,x_0^2)=(1,1)\), as shown in Figure 4.5.5 .
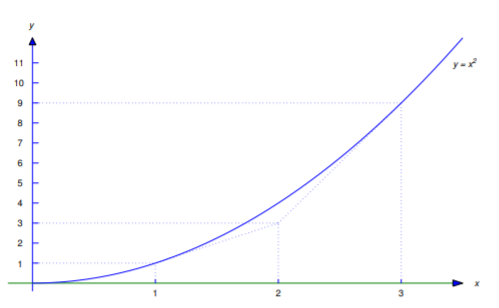
Geometric Problems
We now consider some geometric problems that can be solved by means of differential equations.
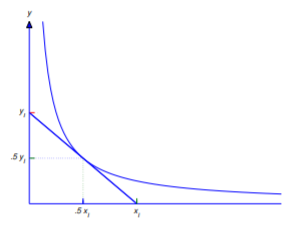
Find curves \(y=y(x)\) such that every point \((x_0,y(x_0))\) on the curve is the midpoint of the line segment with endpoints on the coordinate axes and tangent to the curve at \((x_0,y(x_0))\) (Figure 4.5.6 ).
Solution
The equation of the line tangent to the curve at \(P=(x_0,y(x_0)\) is
\[y=y(x_0)+y'(x_0)(x-x_0). \nonumber\]
If we denote the \(x\) and \(y\) intercepts of the tangent line by \(x_I\) and \(y_I\) (Figure 4.5.6 ), then
\[\label{eq:4.5.14} 0=y(x_0)+y'(x_0)(x_I-x_0)\]
and
\[\label{eq:4.5.15} y_I=y(x_0)-y'(x_0)x_0.\]
From Figure 4.5.6 , \(P\) is the midpoint of the line segment connecting \((x_I,0)\) and \((0,y_I)\) if and only if \(x_I=2x_0\) and \(y_I=2y(x_0)\). Substituting the first of these conditions into Equation \ref{eq:4.5.14} or the second into Equation \ref{eq:4.5.15} yields
\[y(x_0)+y'(x_0)x_0=0. \nonumber\]
Since \(x_0\) is arbitrary we drop the subscript and conclude that \(y=y(x)\) satisfies
\[y+xy'=0, \nonumber\]
which can be rewritten as
\[(xy)'=0. \nonumber\]
Integrating yields \(xy=c\), or
\[y={c\over x}. \nonumber\]
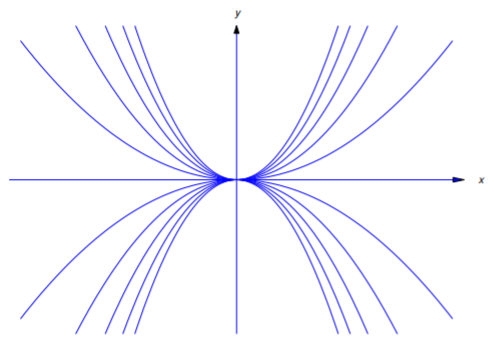
If \(c=0\) this curve is the line \(y=0\), which does not satisfy the geometric requirements imposed by the problem; thus, \(c\ne0\), and the solutions define a family of hyperbolas (Figure 4.5.7 ).
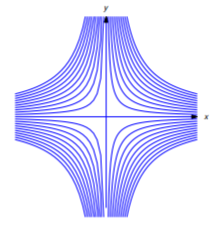
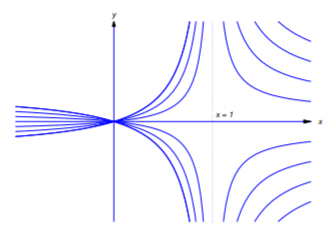
Find curves \(y=y(x)\) such that the tangent line to the curve at any point \((x_0,y(x_0))\) intersects the \(x\)-axis at \((x^2_0,0)\). Figure 4.5.8 illustrates the situation in the case where the curve is in the first quadrant and \(0<x<1\).
Solution
The equation of the line tangent to the curve at \((x_0,y(x_0))\) is
\[y=y(x_0)+y'(x_0)(x-x_0). \nonumber\]
Since \((x^2_0,0)\) is on the tangent line,
\[0=y(x_0)+y'(x_0)(x^2_0-x_0). \nonumber\]
Since \(x_0\) is arbitrary we drop the subscript and conclude that \(y=y(x)\) satisfies
\[y+y'(x^2-x)=0. \nonumber\]
Therefore
\[{y'\over y}=-{1\over x^2-x}=-{1\over x(x-1)}={1\over x}-{1\over x-1},\nonumber\]
so
\[\ln|y|=\ln|x|-\ln|x-1|+k= \ln\left|{x\over x-1}\right|+k,\nonumber\]
and
\[y={cx\over x-1}. \nonumber\]
If \(c=0\), the graph of this function is the \(x\)-axis. If \(c\ne0\), it is a hyperbola with vertical asymptote \(x=1\) and horizontal asymptote \(y=c\). Figure 4.5.9 shows the graphs for \(c\ne0\).
Orthogonal Trajectories
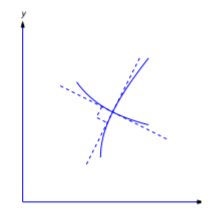
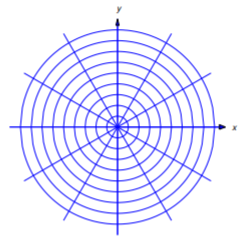
Two curves \(C_1\) and \(C_2\) are said to be orthogonal at a point of intersection \((x_0,y_0)\) if they have perpendicular tangents at \((x_0,y_0)\). (Figure 4.5.10 ). A curve is said to be an orthogonal trajectory of a given family of curves if it is orthogonal to every curve in the family. For example, every line through the origin is an orthogonal trajectory of the family of circles centered at the origin. Conversely, any such circle is an orthogonal trajectory of the family of lines through the origin (Figure 4.5.11 ).
Orthogonal trajectories occur in many physical applications. For example, if \(u=u(x,y)\) is the temperature at a point \((x,y)\), the curves defined by
\[\label{eq:4.5.16} u(x,y)=c\]
are called isothermal curves. The orthogonal trajectories of this family are called heat-flow lines, because at any given point the direction of maximum heat flow is perpendicular to the isothermal through the point. If \(u\) represents the potential energy of an object moving under a force that depends upon \((x,y)\), the curves Equation \ref{eq:4.5.16} are called equipotentials, and the orthogonal trajectories are called lines of force.
From analytic geometry we know that two nonvertical lines \(L_1\) and \(L_2\) with slopes \(m_1\) and \(m_2\), respectively, are perpendicular if and only if \(m_2=-1/m_1\); therefore, the integral curves of the differential equation
\[y'=-{1\over f(x,y)} \nonumber\]
are orthogonal trajectories of the integral curves of the differential equation
\[y'=f(x,y), \nonumber\]
because at any point \((x_0,y_0)\) where curves from the two families intersect the slopes of the respective tangent lines are
\[m_1=f(x_0,y_0)\quad\text{and} \quad m_2=-{1\over f(x_0,y_0)}. \nonumber\]
This suggests a method for finding orthogonal trajectories of a family of integral curves of a first order equation.
- Step 1. Find a differential equation \[y'=f(x,y) \nonumber \] for the given family.
- Step 2. Solve the differential equation \[y'=-{1\over f(x,y)} \nonumber \] to find the orthogonal trajectories.
Find the orthogonal trajectories of the family of circles
\[\label{eq:4.5.17} x^2+y^2=c^2 \quad (c>0).\]
Solution
To find a differential equation for the family of circles we differentiate Equation \ref{eq:4.5.17} implicitly with respect to \(x\) to obtain
\[2x+2yy'=0, \nonumber\]
or
\[y'=-{x\over y}. \nonumber\]
Therefore the integral curves of
\[y'={y\over x} \nonumber\]
are orthogonal trajectories of the given family. We leave it to you to verify that the general solution of this equation is
\[y=kx, \nonumber\]
where \(k\) is an arbitrary constant. This is the equation of a nonvertical line through \((0,0)\). The \(y\) axis is also an orthogonal trajectory of the given family. Therefore every line through the origin is an orthogonal trajectory of the given family Equation \ref{eq:4.5.17} (Figure 4.5.11 ). This is consistent with the theorem of plane geometry which states that a diameter of a circle and a tangent line to the circle at the end of the diameter are perpendicular.
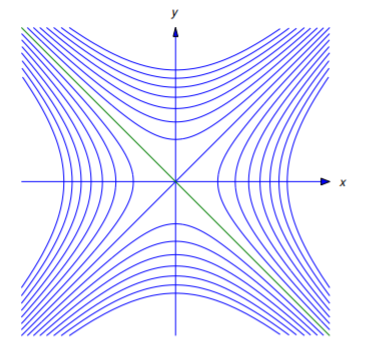
Find the orthogonal trajectories of the family of hyperbolas
\[\label{eq:4.5.18} xy=c \quad (c\ne0)\]
(Figure 4.5.7 ).
Solution
Differentiating Equation \ref{eq:4.5.18} implicitly with respect to \(x\) yields
\[y+xy'=0, \nonumber\]
or
\[y'=-{y\over x}; \nonumber\]
thus, the integral curves of
\[y'={x\over y} \nonumber\]
are orthogonal trajectories of the given family. Separating variables yields
\[y'y=x \nonumber\]
and integrating yields
\[y^2-x^2=k, \nonumber\]
which is the equation of a hyperbola if \(k \ne0\), or of the lines \(y=x\) and \(y=-x\) if \(k=0\) (Figure 4.5.12 ).
Find the orthogonal trajectories of the family of circles defined by
\[\label{eq:4.5.19} (x-c)^2+y^2=c^2 \quad (c\ne0).\]
These circles are centered on the \(x\)-axis and tangent to the \(y\)-axis (Figure 4.5.13 a).
Solution
Multiplying out the left side of Equation \ref{eq:4.5.19} yields
\[\label{eq:4.5.20} x^2-2cx+y^2=0,\]
and differentiating this implicitly with respect to \(x\) yields
\[\label{eq:4.5.21} 2(x-c)+2yy'=0.\]
From Equation \ref{eq:4.5.20},
\[c={x^2+y^2\over2x}, \nonumber \]
so
\[x-c=x-{x^2+y^2\over2x}={x^2-y^2\over2x}. \nonumber\]
Substituting this into Equation \ref{eq:4.5.21} and solving for \(y'\) yields
\[\label{eq:4.5.22} y'={y^2-x^2\over2xy}.\]
The curves defined by Equation \ref{eq:4.5.19} are integral curves of Equation \ref{eq:4.5.22}, and the integral curves of
\[y'={2xy\over x^2-y^2} \nonumber\]
are orthogonal trajectories of the family Equation \ref{eq:4.5.19}. This is a homogeneous nonlinear equation, which we studied in Section 2.4. Substituting \(y=ux\) yields
\[u'x+u={2x(ux)\over x^2-(ux)^2}={2u\over1-u^2}, \nonumber\]
so
\[u'x={2u\over1-u^2}-u={u(u^2+1)\over1-u^2}, \nonumber\]
Separating variables yields
\[{1-u^2\over u(u^2+1)}u'={1\over x}, \nonumber\]
or, equivalently,
\[\left[{1\over u}-{2u\over u^2+1}\right]u'={1\over x}. \nonumber\]
Therefore
\[\ln |u|-\ln (u^2+1)=\ln |x|+k. \nonumber\]
By substituting \(u=y/x\), we see that
\[\ln|y|-\ln|x|-\ln(x^2+y^2)+\ln(x^2)=\ln|x|+k, \nonumber\]
which, since \(\ln(x^2)=2\ln|x|\), is equivalent to
\[\ln|y|-\ln(x^2+y^2)=k, \nonumber\]
or
\[|y|=e^k(x^2+y^2). \nonumber\]
To see what these curves are we rewrite this equation as
\[x^2+|y|^2-e^{-k}|y|=0 \nonumber\]
and complete the square to obtain
\[x^2+(|y|-e^{-k}/2)^2=(e^{-k}/2)^2. \nonumber\]
This can be rewritten as
\[x^2+(y-h)^2=h^2, \nonumber\]
where
\[h=\left\{\begin{array}{rl} {e^{-k}\over2}&\text{ if } y\ge 0,\\[4pt]-{e^{-k}\over2}&\mbox{ if } y\le0. \end{array}\right. \nonumber\]
Thus, the orthogonal trajectories are circles centered on the \(y\) axis and tangent to the \(x\) axis (Figure 4.5.13 (b)). The circles for which \(h>0\) are above the \(x\)-axis, while those for which \(h<0\) are below.