11.2E: Fourier Series I (Exercises)
- Page ID
- 18285
Q11.2.1
1. Prove Theorem 11.1.5.
Q11.2.2
In Exercises 11.2.2-11.2.16 find the Fourier series of \(f\) on \([-L,L]\) and determine its sum for \(-L\leq x\leq L\). Graph \(f\) for Exercises 11.2.2, 11.2.6, 11.2.8, 11.2.15, and 11.2.16 and \[F_{m}(x)=a_{0}+\sum _{n=1}^{m}\left( a_{n}\cos\frac{n\pi x}{L}+b_{n}\sin\frac{n\pi x}{L} \right)\nonumber \] on the same axes for variable values of \(m\).
2. \(L=1\); \(f(x)=2-x\)
3. \(L=\pi\); \(f(x)=2x-3x^2\)
4. \(L=1\); \(f(x)=1-3x^2\)
5. \(L=\pi\); \(f(x)=|\sin x|\)
6. \(L=\pi\); \(f(x)=x\cos x\)
7. \(L=\pi\); \(f(x)=|x|\cos x\)
8. \(L=\pi\); \(f(x)=x\sin x\)
9. \(L=\pi\); \(f(x)=|x|\sin x\)
10. \(L=1\); \(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ \cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)
11. \(L=1\); \(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ x\cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)
12. \(L=1\); \(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ \sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)
13. \(L=1\); \(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ |\sin\pi x|,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)
14. \(L=1\); \(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ x\sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)
15. \(L=4\); \(f(x)= \left\{\begin{array}{cl} 0,&-4<x<0,\\x,&\phantom{-}0<x<4 \end{array}\right.\)
16. \(L=1\); \(f(x)= \left\{\begin{array}{cl} x^2,&-1< x<0, \\1-x^2,&\phantom{-}0<x<1 \end{array}\right.\)
Q11.2.3
17. Verify the Gibbs phenomenon for \(f(x)= \left\{\begin{array}{rl} 2,&-2< x< -1,\\1,&-1<x<1,\\-1,&\phantom{-}1< x<2. \end{array}\right.\)
18. Verify the Gibbs phenomenon for \(f(x)= \left\{\begin{array}{rl} 2,&-3< x< -2,\\3,&-2<x<2,\\1,&\phantom{-}2< x<3. \end{array}\right.\)
19. Deduce from Example 11.2.5 that
\[\sum_{n=0}^\infty{1\over(2n+1)^2}={\pi^2\over 8}.\nonumber \]
20.
- Find the Fourier series of \(f(x)=e^x\) on \([-\pi,\pi]\).
- Deduce from (a) that \[\sum_{n=0}^\infty{1\over n^2+1}={\pi\coth\pi-1\over2}.\nonumber \]
21. Find the Fourier series of \(f(x)=(x-\pi)\cos x\) on \([-\pi,\pi]\).
22. Find the Fourier series of \(f(x)=(x-\pi)\sin x\) on \([-\pi,\pi]\).
23. Find the Fourier series of \(f(x)=\sin kx\) (\(k\ne\) integer) on \([-\pi,\pi]\).
24. Find the Fourier series of \(f(x)=\cos kx\) (\(k\ne\) integer) on \([-\pi,\pi]\).
25.
- Suppose \(g'\) is continuous on \([a,b]\) and \(\omega\ne0\). Use integration by parts to show that there’s a constant \(M\) such that \[\left|\int_a^bg(x)\cos\omega x\,dx\right|\le{M\over\omega} \quad \text{and} \quad \left|\int_a^bg(x)\sin\omega x\,dx\right|\le{M\over\omega},\quad \omega>0.\nonumber\]
- Show that the conclusion of (a) also holds if \(g\) is piecewise smooth on \([a,b]\). (This is a special case of Riemann’s Lemma.
- We say that a sequence \(\{\alpha_n\}_{n=1}^\infty\) is of order \(n^{-k}\) and write \(\alpha_n=O(1/n^k)\) if there’s a constant \(M\) such that \[|\alpha_n|<{M\over n^k},\quad n=1,2,3,\dots.\nonumber \] Let \(\{a_n\}_{n=1}^\infty\) and \(\{b_n\}_{n=1}^\infty\) be the Fourier coefficients of a piecewise smooth function. Conclude from (b) that \(a_n=O(1/n)\) and \(b_n=O(1/n)\).
26.
- Suppose \(f(-L)=f(L)\), \(f'(-L)=f'(L)\), \(f'\) is continuous, and \(f''\) is piecewise continuous on \([-L,L]\). Use Theorem 11.2.4 and integration by parts to show that \[f(x)=a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right),\quad -L\le x\le L,\nonumber \] with \[a_0={1\over 2L}\int_{-L}^L f(x)\,dx,\nonumber \] \[a_n= -{L\over n^2\pi^2}\int_{-L}^L f''(x)\cos{n\pi x\over L}\,dx,\quad \text{and} \quad b_n=-{L\over n^2\pi^2}\int_{-L}^L f''(x)\sin{n\pi x\over L}\,dx,\,n\ge1.\nonumber \]
- Show that if, in addition to the assumptions in (a), \(f''\) is continuous and \(f'''\) is piecewise continuous on \([-L,L]\), then \[a_n={L^2\over n^3\pi^3}\int_{-L}^Lf'''(x)\sin{n\pi x\over L}\,dx.\nonumber \]
27. Show that if \(f\) is integrable on \([-L,L]\) and \[f(x+L)=f(x),\quad -L<x<0\nonumber \] (Figure 11.2.8), then the Fourier series of \(f\) on \([-L,L]\) has the form \[A_0+\sum_{n=1}^\infty\left(A_n\cos{2n\pi\over L}+B_n\sin{2n\pi\over L}\right)\nonumber \] where \[A_0={1\over L}\int_0^Lf(x)\,dx,\nonumber \] and \[A_n={2\over L}\int_0^Lf(x)\cos{2n\pi x\over L}\,dx, \quad B_n={2\over L}\int_0^Lf(x)\sin{2n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
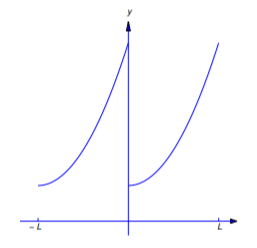
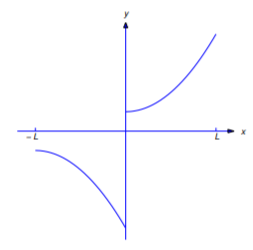
28. Show that if \(f\) is integrable on \([-L,L]\) and
\[f(x+L)=-f(x),\quad -L<x<0\nonumber \]
(Figure 11.2.9), then the Fourier series of \(f\) on \([-L,L]\) has the form
\[\sum_{n=1}^\infty\left(A_n\cos{(2n-1)\pi x\over L}+B_n\sin{(2n-1)\pi x\over L}\right),\nonumber \]
where
\[A_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over L}\,dx \quad \text{and} \quad B_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
29. Suppose \(\phi_1\), \(\phi_2\), …, \(\phi_m\) are orthogonal on \([a,b]\) and
\[\int_a^b\phi_n^2(x)\,dx\ne0,\quad n=1,2,\dots,m.\nonumber \]
If \(a_1\), \(a_2\), …, \(a_m\) are arbitrary real numbers, define
\[P_m=a_1\phi_1+a_2\phi_2+\cdots+a_m\phi_m.\nonumber \]
Let
\[F_m=c_1\phi_1+c_2\phi_2+\cdots+c_m\phi_m,\nonumber \]
where
\[c_n={\int_a^bf(x)\phi_n(x)\,dx\over\int_a^b\phi_n^2(x)\,dx};\nonumber \]
that is, \(c_1\), \(c_2\), …, \(c_m\) are Fourier coefficients of \(f\).
- Show that \[\int_a^b(f(x)-F_m(x))\phi_n(x)\,dx=0,\quad n=1,2,\dots,m.\nonumber \]
- Show that \[\int_a^b(f(x)-F_m(x))^2\,dx\le \int_a^b(f(x)-P_m(x))^2\,dx,\nonumber \] with equality if and only if \(a_n=c_n\), \(n=1,2,\dots, m\).
- Show that \[\int_a^b(f(x)-F_m(x))^2\,dx=\int_a^bf^2(x)\,dx-\sum_{n=1}^mc_n^2\int_a^b \phi_n^2\,dx.\nonumber \]
- Conclude from (c) that \[\sum_{n=1}^m c_n^2\int_a^b\phi_n^2(x)\,dx\le \int_a^bf^2(x)\,dx.\nonumber \]
30. If \(A_0\), \(A_1\), …, \(A_m\) and \(B_1\), \(B_2\), …, \(B_m\) are arbitrary constants we say that
\[P_m(x)=A_0+\sum_{n=1}^m\left(A_n\cos{n\pi x\over L}+B_n\sin{n\pi x\over L}\right)\nonumber \]
is a trigonometric polynomial of degree \(\le m\).
Now let
\[a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right)\nonumber \]
be the Fourier series of an integrable function \(f\) on \([-L,L]\), and let
\[F_m(x)= a_0+\sum_{n=1}^m\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right).\nonumber \]
- Conclude from Exercise 11.2.29b that \[\int_{-L}^L(f(x)-F_m(x))^2\,dx\le \int_{-L}^L(f(x)-P_m(x))^2\,dx,\nonumber \] with equality if and only if \(A_n=a_n\), \(n=0\), \(1\), …, \(m\), and \(B_n=b_n\), \(n=1\), \(2\), …, \(m\).
- Conclude from Exercise 11.2.29d that \[2a_0^2+\sum_{n=1}^m(a_n^2+b_n^2)\le{1\over L}\int_{-L}^Lf^2(x)\,dx\nonumber \] for every \(m\ge0\).
- Conclude from (b) that \(\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=0\).


