4.4: A Method of Riemann
- Page ID
- 2151
Riemann's method provides a formula for the solution of the following Cauchy initial value problem for a hyperbolic equation of second order in two variables. Let
$${\mathcal S}:\ \ x=x(t), y=y(t),\ \ t_1\le t \le t_2,\]
be a regular curve in \(\mathbb{R}^2\), that is, we assume \(x,\ y\in C^1[t_1,t_2]\) and \(x'^2+y'^2\not=0\). Set
$$Lu:=u_{xy}+a(x,y)u_x+b(x,y)u_y+c(x,y)u,\]
where \(a,\ b\in C^1\) and \(c,\ f\in C\) in a neighborhood of \({\mathcal S}\). Consider the initial value problem
\begin{eqnarray}
\label{riem1}
Lu&=&f(x,y)\\
\label{riem2}
u_0(t)&=&u(x(t),y(t))\\
\label{riem3}
p_0(t)&=&u_x(x(t),y(t))\\
\label{riem4}
q_0(t)&=&u_y(x(t),y(t)),
\end{eqnarray}
where \(f\in C\) in a neighbourhood of \({\mathcal S}\) and \(u_0,\ p_0,\ q_0\in C^1\) are given.
We assume:
- \(u_0'(t)=p_0(t)x'(t)+q_0(t)y'(t)\) (strip condition),
- \({\mathcal S}\) is not a characteristic curve. Moreover assume that the characteristic curves, which are lines here and are defined by \(x=const.\) and \(y=const.\), have at most one point of intersection with \({\mathcal S}\), and such a point is not a touching point, i. e., tangents of the characteristic and \({\mathcal S}\) are different at this point.
We recall that the characteristic equation to (\ref{riem1}) is \(\chi_x\chi_y=0\) which is satisfied if \(\chi_x(x,y)=0\) or \(\chi_y(x,y)=0\). One family of characteristics associated to these first partial differential of first order is defined by \(x'(t)=1,\ y'(t)=0\), see Chapter 2.
Assume \(u,\ v\in C^1\) and that \(u_{xy},\ v_{xy}\) exist and are continuous. Define the adjoint differential expression by
$$Mv=v_{xy}-(av)_x-(bv)_y+cv.\]
We have
\begin{equation}
\label{riem5}
2(vLu-uMv)=(u_xv-v_xu+2buv)_y+(u_yv-v_yu+2auv)_x.
\end{equation}
Set
\begin{eqnarray*}
P&=&-(u_xv-x_xu+2buv)\\
Q&=&u_yv-v_yu+2auv.
\end{eqnarray*}
From (\ref{riem5}) it follows for a domain \(\Omega\in\mathbb{R}^2\)
\begin{eqnarray}
2\int_\Omega\ (vLu-uMv)\ dxdy&=&\int_\Omega\ (-P_y+Q_x)\ dxdy\nonumber\\
\label{riem6}
&=&\oint\ Pdx+Qdy,
\end{eqnarray}
where integration in the line integral is anticlockwise. The previous equation follows from Gauss theorem or after integration by parts:
$$\int_\Omega\ (-P_y+Q_x)\ dxdy=\int_{\partial\Omega}\ (-Pn_2+Qn_1)\ ds,\]
where \(n=(dy/ds,-dx/ds)\), \(s\) arc length, \((x(s),y(s))\) represents \(\partial\Omega\).
Assume \(u\) is a solution of the initial value problem (\ref{riem1})-(\ref{riem4}) and suppose that \(v\) satisfies
$$Mv=0\ \ \mbox{in}\ \Omega.\]
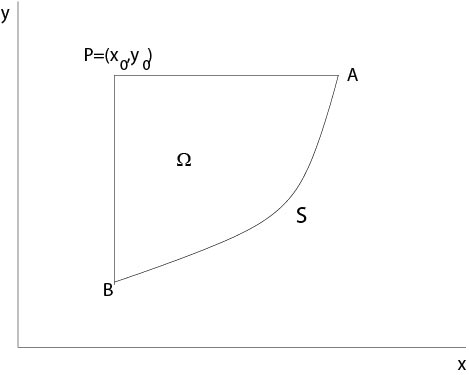
Figure 4.4.1: Riemann's method, domain of integration
Then, if we integrate over a domain \(\Omega\) as shown in Figure 4.4.1, it follows from (\ref{riem6}) that
\begin{equation}
\label{riem7}
2\int_\Omega\ vf\ dxdy=\int_{BA}\ Pdx+Qdy+\int_{AP}\ Pdx+Qdy+\int_{PB}\ Pdx+Qdy.
\end{equation}
The line integral from \(B\) to \(A\) is known from initial data, see the definition of \(P\) and \(Q\).
Since
$$u_xv-v_xu+2buv=(uv)_x+2u(bv-v_x),\]
it follows
\begin{eqnarray*}
\int_{AP} Pdx+Qdy&=&-\int_{AP} \left((uv)_x+2u(bv-v_x)\right)\ dx\\
&=&-(uv)(P)+(uv)(A)-\int_{AP}\ 2u(bv-v_x)\ dx.
\end{eqnarray*}
By the same reasoning we obtain for the third line integral
\begin{eqnarray*}
\int_{PB} Pdx+Qdy&=&\int_{PB} \left((uv)_y+2u(av-v_y)\right)\ dy\\
&=&(uv)(B)-(uv)(P)+\int_{PB} 2u(av-v_y)\ dy.
\end{eqnarray*}
Combining these equations with (\ref{riem6}), we get
\begin{eqnarray}
2v(P)u(P)&=&\int_{BA} (u_xv-v_x+2buv)\ dx-(u_yv-v_yu+2auv)\ dy\nonumber\\
&&+u(A)v(A)+u(B)v(B)+2\int_{AP}u(bv-v_x)\ dx\nonumber\\
\label{riemend}
&&+2\int_{PB}u(av-v_y)\ dy-2\int_\Omega fv\ dxdy.
\end{eqnarray}
Let \(v\) be a solution of the initial value problem, see Figure 4.2.2 for the definition of domain \(D(P)\),
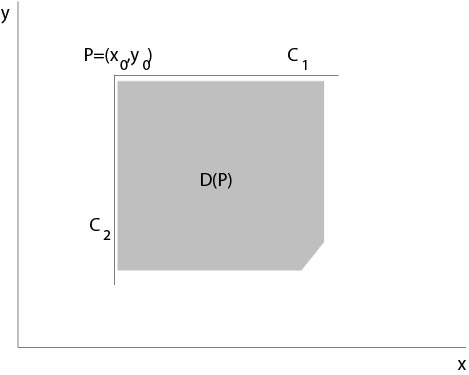
Figure 4.4.2: Definition of Riemann's function
\begin{eqnarray}
\label{riem9}
Mv&=&0\ \ \mbox{in}\ D(P)\\
\label{riem10}
bv-v_x&=&0\ \ \mbox{on}\ C_1\\
\label{riem11}
av-v_y&=&0\ \ \mbox{on}\ C_2\\
\label{riem12}
v(P)&=&1.
\end{eqnarray}
Assume \(v\) satisfies (\ref{riem9})-(\ref{riem12}), then
\begin{eqnarray*}
2u(P)&=&u(A)v(A)+u(B)v(B)-2\int_\Omega\ fv\ dxdy\\
&&=\int_{BA}(u_xv-v_x+2buv)\ dx-(u_yv-v_yu+2auv)\ dy,
\end{eqnarray*}
where the right hand side is known from given data.
A function \(v=v(x,y;x_0,y_0)\) satisfying (\ref{riem9})-(\ref{riem12}) is called Riemann's function.
Remark. Set \(w(x,y)=v(x,y;x_0,y_0)\) for fixed \(x_0,\ y_0\). Then (\ref{riem9})-(\ref{riem12}) imply
\begin{eqnarray*}
w(x,y_0)&=&\exp\left(\int_{x_0}^x\ b(\tau,y_0)\ d\tau\right)\ \ \mbox{on}\ C_1,\\
w(x_0,y)&=&\exp\left(\int_{y_0}^y\ a(x_0,\tau)\ d\tau\right)\ \ \mbox{on}\ C_2.
\end{eqnarray*}
Example 4.4.1:
\(u_{xy}=f(x,y)\), then a Riemann function is \(v(x,y)\equiv 1\).
Example 4.4.2:
Consider the telegraph equation of Chapter 3
$$\varepsilon \mu u_{tt}=c^2\triangle_xu-\lambda\mu u_t,\]
where \(u\) stands for one coordinate of electric or magnetic field.
Introducing
$$u=w(x,t)e^{\kappa t},\]
where \(\kappa=-\lambda/(2\varepsilon)\), we arrive at
$$w_{tt}=\frac{c^2}{\varepsilon\mu}\triangle_xw-\frac{\lambda^2}{4\epsilon^2}.\]
Stretching the axis and transform the equation to the normal form we get finally the following equation, the new function is denoted by \(u\) and the new variables are denoted by \(x,y\) again,
$$u_{xy}+cu=0,\]
with a positive constant \(c\). We make the ansatz for a Riemann function
$$v(x,y;x_0,y_0)=w(s),\ \ s=(x-x_0)(y-y_0)\]
and obtain
$$sw''+w'+cw=0.\]
Substitution \(\sigma=\sqrt{4cs}\) leads to Bessel's differential equation
$$\sigma^2 z''(\sigma)+\sigma z'(\sigma)+\sigma^2 z(\sigma)=0,\]
where \(z(\sigma)=w(\sigma^2/(4c))\). A solution is
$$J_0(\sigma)=J_0\left(\sqrt{4c(x-x_0)(y-y_0)}\right)\]
which defines a Riemann function since \(J_0(0)=1\).
Remark. Bessel's differential equation is
$$x^2y''(x)+xy'(x)+(x^2-n^2)y(x)=0,\]
where \(n\in\mathbb{R}^1\). If \(n\in{\mathbb N}\cup\{0\}\), then solutions are given by Bessel functions. One of the two linearly independent solutions is bounded at 0. This bounded solution is the Bessel function \(J_n(x)\) of first kind and of order \(n\), see [1], for example.
Contributors and Attributions
Integrated by Justin Marshall.


