7.4: Green's Function for \(\Delta\)
- Page ID
- 2165
Theorem 7.1 says that each harmonic function satisfies
\begin{equation}
\label{green1}
u(x)=\int_{\partial\Omega}\left(\gamma (y,x)\frac{\partial u(y)}{\partial n_y}-u(y)\frac{\partial \gamma(y,x)}{\partial n_y}\right)\ dS_y,
\end{equation}
where \(\gamma(y,x)\) is a fundamental solution. In general, \(u\) does not satisfies the boundary condition in the above boundary value problems. Since \(\gamma=s+\phi\), see Section 7.2, where \(\phi\) is an arbitrary harmonic function for each fixed \(x\), we try to find a \(\phi\) such that \(u\) satisfies also the boundary condition.
Consider the Dirichlet problem, then we look for a \(\phi\) such that
\begin{equation}
\label{green2}
\gamma(y,x)=0,\ \ y\in\partial\Omega,\ x\in\Omega.
\end{equation}
Then
$$
u(x)=-\int_{\partial\Omega}\ \frac{\partial \gamma(y,x)}{\partial n_y}u(y)\ dS_y,\ \ x\in\Omega.
$$
Suppose that \(u\) achieves its boundary values \(\Phi\) of the Dirichlet problem, then
\begin{equation}
\label{green3}
u(x)=-\int_{\partial\Omega}\ \frac{\partial \gamma(y,x)}{\partial n_y}\Phi(y)\ dS_y,
\end{equation}
We claim that this function solves the Dirichlet problem (7.3.1.1), (7.3.1.2).
A function \(\gamma(y,x)\) which satisfies (\ref{green2}), and some additional assumptions, is called Green's function. More precisely, we define a Green function as follows.
Definition. A function \(G(y,x)\), \(y,\ x\in\overline{\Omega}\), \(x\not= y\), is called Green function associated to \(\Omega\) and to the Dirichlet problem (7.3.1.1), (7.3.1.2) if for fixed \(x\in\Omega\), that is we consider \(G(y,x)\) as a function of \(y\), the following properties hold:
(i) \(G(y,x)\in C^2(\Omega\setminus\{x\})\cap C(\overline{\Omega}\setminus\{x\})\), \(\triangle_yG(y,x)=0,\ \ x\not=y\).
(ii) \(G(y,x)-s(|x-y|)\in C^2(\Omega)\cap C(\overline{\Omega})\).
(iii) \(G(y,x)=0\) if \(y\in\partial\Omega\), \(x\not=y\).
Remark. We will see in the next section that a Green function exists at least for some domains of simple geometry. Concerning the existence of a Green function for more general domains see [13].
It is an interesting fact that we get from (i)-(iii) of the above definition two further important properties, provided \(\Omega\) is bounded, sufficiently regular and connected.
Proposition 7.7. A Green function has the following properties. In the case \(n=2\) we assume {\rm diam} \(\Omega<1\).
(A) \(G(x,y)=G(y,x)\)\ \ (symmetry).
(B) \(0<G(x,y)<s(|x-y|), \ \ x,\ y\in\Omega,\ x\not=y\).
Proof. (A) Let \(x^{(1)},\ x^{(2)}\in\Omega\). Set \(B_i=B_\rho(x^{(i)})\), \(i=1,\ 2\). We assume \(\overline{B_i}\subset\Omega\) and \(B_1\cap B_2=\emptyset\). Since \(G(y,x^{(1)})\) and \(G(y,x^{(2)})\) are harmonic in \(\Omega\setminus\left(\overline{B_1}\cup\overline{B_2}\right)\) we obtain from Green's identity, see Figure 7.4.1 for notations,
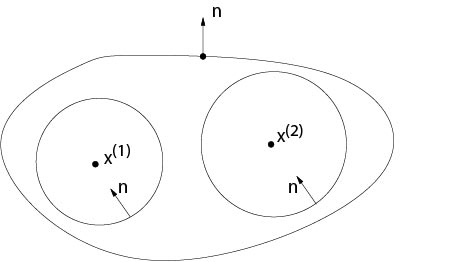
Figure 7.4.1: Proof of Proposition 7.7
\begin{eqnarray*}
0&=&\int_{\partial\left(\Omega\setminus(\overline{B_1}\cup\overline{B_2})\right)}
\bigg(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})\\
&& \qquad \qquad \qquad \qquad\qquad \qquad -G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\bigg) dS_y\\
&=&\int_{\partial\Omega}
\left(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})-G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\right) dS_y\\
&+&\int_{\partial B_1}
\left(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})-G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\right) dS_y\\
&+&\int_{\partial B_2}
\left(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})-G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\right) dS_y.
\end{eqnarray*}
The integral over \(\partial\Omega\) is zero because of property (iii) of a Green function, and
\begin{eqnarray*}
\int_{\partial B_1}\
\bigg(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})&-&G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\bigg) dS_y\\
&\to& G(x^{(1)},x^{(2)}),\\
\int_{\partial B_2}\
\bigg(G(y,x^{(1)})\frac{\partial}{\partial n_y}G(y,x^{(2)})&-&G(y,x^{(2)})\frac{\partial}{\partial n_y}G(y,x^{(1)})\bigg)\ dS_y\\
&\to&
-G(x^{(2)},x^{(1)})
\end{eqnarray*}
as \(\rho\to 0\).
This follows by considerations as in the proof of Theorem 7.1.
(B) Since
$$
G(y,x)=s(|x-y|)+\phi(y,x)
$$
and \(G(y,x)=0\) if \(y\in\partial\Omega\) and \(x\in\Omega\) we have for \(y\in\partial\Omega\)
$$
\phi(y,x)=-s(|x-y|).
$$
From the definition of \(s(|x-y|)\) it follows that \(\phi(y,x)< 0\) if \(y\in\partial\Omega\). Thus, since \(\triangle_y\phi=0\) in \(\Omega\), the maximum-minimum principle implies that \(\phi(y,x)<0\)
for all \(y,~x\in\Omega\). Consequently
$$
G(y,x)<s(|x-y|),\ \ x,\ y\in\Omega,\ x\not=y.
$$
It remains to show that
$$
G(y,x)>0,\ \ x,\ y\in\Omega,\ x\not=y.
$$
Fix \(x\in\Omega\) and let \(B_\rho(x)\) be a ball such that \(B_\rho(x)\subset\Omega\) for all \(0<\rho<\rho_0\). There is a sufficiently small \(\rho_0>0\) such that for each \(\rho\), \(0<\rho<\rho_0\),
$$
G(y,x)>0\ \ \mbox{for all}\ y\in\overline{B_\rho(x)},\ x\not=y,
$$
see property (iii) of a Green function. Since
\begin{eqnarray*}
\triangle_y G(y,x)&=&0\ \ \mbox{in}\ \Omega\setminus\overline{B_\rho(x)}\\
G(y,x)&>&0\ \ \mbox{if}\ y\in\partial B_\rho(x)\\
G(y,x)&=&0\ \ \mbox{if}\ y\in\partial\Omega
\end{eqnarray*}
it follows from the maximum-minimum principle that
$$
G(y,x)>0\ \ \mbox{on}\ \Omega\setminus\overline{B_\rho(x)}.
\]
\(\Box\)


