4.7: Convergence of Fourier series
- Page ID
- 8351
The final subject we shall consider is the convergence of Fourier series. I shall show two examples, closely linked, but with radically different behaviour.
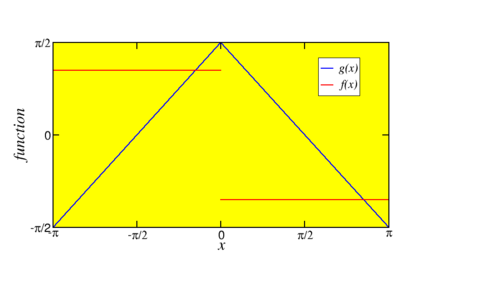
- A square wave,
\(f(x)= 1\) for \(-\pi < x < 0\); \(f(x)= -1\) for \(0 < x < \pi\). - a triangular wave,
\(g(x)= \pi/2+x\) for \(-\pi < x < 0\); \(g(x)= \pi/2-x\) for \(0 < x < \pi\).
Note that \(f\) is the derivative of \(g\).
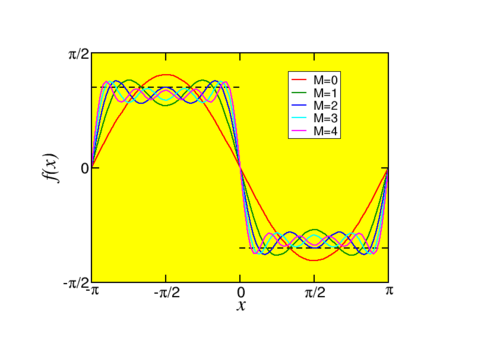
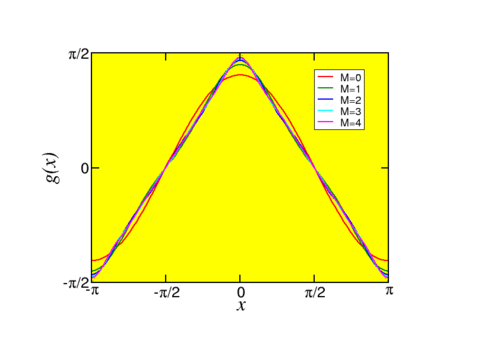
It is not very hard to find the relevant Fourier series, \[\begin{aligned} f(x) & = & -\frac{4}{\pi} \sum_{m=0}^\infty \frac{1}{2m+1} \sin (2m+1) x,\\ g(x) & = & \frac{4}{\pi} \sum_{m=0}^\infty \frac{1}{(2m+1)^2} \cos (2m+1) x.\end{aligned} \nonumber \] Let us compare the partial sums, where we let the sum in the Fourier series run from \(m=0\) to \(m=M\) instead of \(m=0\ldots\infty\). We note a marked difference between the two cases. The convergence of the Fourier series of \(g\) is uneventful, and after a few steps it is hard to see a difference between the partial sums, as well as between the partial sums and \(g\). For \(f\), the square wave, we see a surprising result: Even though the approximation gets better and better in the (flat) middle, there is a finite (and constant!) overshoot near the jump. The area of this overshoot becomes smaller and smaller as we increase \(M\). This is called the Gibbs phenomenon (after its discoverer). It can be shown that for any function with a discontinuity such an effect is present, and that the size of the overshoot only depends on the size of the discontinuity! A final, slightly more interesting version of this picture, is shown in Fig. \(\PageIndex{3}\).