8.3: Putting it all together
- Page ID
- 8338
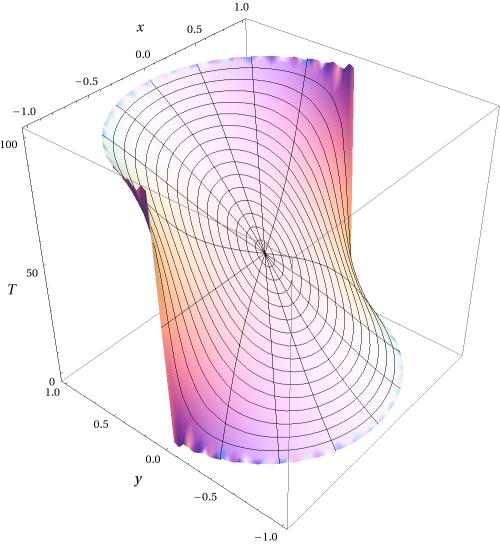
In summary, we have \[u(\rho,\phi) = \frac{A_0}{2} + \sum_{n=1}^\infty \rho^n \left(A_n\cos n\phi+B_n\sin n \phi \right). \nonumber \] The one remaining boundary condition can now be used to determine the coefficients \(A_n\) and \(B_n\), \[\begin{aligned} U(c,\phi) &= \frac{A_0}{2} + \sum_{n=1}^\infty c^n \left(A_n\cos n\phi+B_n\sin n \phi \right)\nonumber\\ &= \begin{cases} 100 & \text{if $0 < \phi < \pi$} \\ 0 & \text{if $\pi < \phi < 2\pi$} \end{cases}\quad.\end{aligned} \nonumber \] We find \[\begin{aligned} A_0 &= \frac{1}{\pi} \int_0^\pi 100\, d\phi = 100, \nonumber\\ c^n A_n &= \frac{1}{\pi}\int_0^\pi 100\cos n\phi\, d\phi = \frac{100}{n\pi} \sin(n\phi)|^\pi_0=0,\nonumber\\ c^n B_n &= \frac{1}{\pi}\int_0^\pi 100\sin n\phi\, d\phi = -\frac{100}{n\pi} \cos(n\phi)|^\pi_0 \nonumber\\&= \begin{cases} 200/(n\pi) & \text{if $n$ is odd}\\ 0 & \text{if $n$ is even} \end{cases}\quad.\end{aligned} \nonumber \] In summary \[u(\rho,\phi) = 50 + \frac{200}{\pi} \sum_{n~\rm odd} \left(\frac{\rho}{c}\right)^n \frac{\sin n \phi}{n}. \label{eq:T0-100} \] We clearly see the dependence of \(u\) on the pure number \(r/c\), rather than \(\rho\). A three dimensional plot of the temperature is given in Fig. \(\PageIndex{1}\).