10.8: Fourier-Bessel Series
- Page ID
- 8326
So how can we determine in general the coefficients in the Fourier-Bessel series
\[f(\rho) = \sum_{j=1}^\infty C_j J_\nu(\alpha_j \rho)? \nonumber \]
The corresponding self-adjoint version of Bessel’s equation is easily found to be (with \(R_j(\rho) = J_\nu(\alpha_j\rho)\))
\[(\rho R_j')' + (\alpha_j^2\rho - \frac{\nu^2}{\rho}) R_j = 0. \nonumber \]
Where we assume that \(f\) and \(R\) satisfy the boundary condition
\[\begin{aligned} b_1 f(c) + b_2 f'(c) &= 0 \nonumber\\ b_1 R_j(c) + b_2 R_j'(c) & = & 0 \end{aligned} \nonumber \]
From Sturm-Liouville theory we do know that \[\int_0^c \rho J_\nu(\alpha_i \rho) J_\nu(\alpha_j \rho) = 0 \;\;{\rm if\ }i \neq j, \nonumber \] but we shall also need the values when \(i=j\)!
Let us use the self-adjoint form of the equation, and multiply with \(2 \rho R'\), and integrate over \(\rho\) from \(0\) to \(c\),
\[\int_0^c \left[(\rho R_j')' + (\alpha_j^2\rho - \frac{\nu^2}{\rho}) R_j \right]2 \rho R_j' d\rho = 0. \nonumber \]
This can be brought to the form (integrate the first term by parts, bring the other two terms to the right-hand side)
\[\begin{aligned} \int_0^c \frac{d}{d\rho}\left(\rho R_j'\right)^2 d\rho &= 2 \nu^2 \int_0^c R_j R_j' d\rho -2\alpha_j^2 \int_0^c \rho^2 R_j R_j' d\rho\\ \left.\left(\rho R_j'\right)^2\right|^c_0 &= \left.\nu^2 R_j^2\right|^c_0 - 2\alpha_j^2 \int_0^c \rho^2 R_j R_j' d\rho.\end{aligned} \nonumber \]
The last integral can now be done by parts: \[\begin{aligned} 2 \int_0^c\rho^2 R_j R_j' d\rho &= -2 \int_0^c\rho R_j^2 d\rho +\left. \rho R_j^2 \right|^c_0.\end{aligned} \nonumber \]
So we finally conclude that
\[2 \alpha_j^2 \int_0^c\rho R_j^2 d\rho = \left[\left(\alpha_j^2\rho^2 - \nu^2 \right) R_j^2+\left(\rho R_j'\right)^2 \right|^c_0. \nonumber \]
In order to make life not too complicated we shall only look at boundary conditions where \(f(c)=R(c)=0\). The other cases (mixed or purely \(f'(c)=0\)) go very similar! Using the fact that \(R_j(r) = J_\nu(\alpha_j \rho)\), we find \[R'_j=\alpha_j J'_\nu(\alpha_j \rho). \nonumber \] We conclude that
\[\begin{aligned} 2 \alpha_j^2 \int_0^c\rho^2 R_j^2 d\rho &= \left[ \left(\rho \alpha_j J'_\nu(\alpha_j\rho)\right)^2 \right|^c_0 \nonumber\\ &= {c^2}\alpha_j^2 \left(J'_\nu(\alpha_j c)\right)^2 \nonumber\\ &= {c^2}\alpha_j^2 \left(\frac{\nu}{\alpha_j c} J_\nu(\alpha_j c) -J_{\nu+1}(\alpha_j c)\right)^2 \nonumber\\ &= {c^2}\alpha_j^2 \left( J_{\nu+1}(\alpha_j c)\right)^2 ,\end{aligned} \nonumber \]
We thus finally have the result \[\int_0^c\rho^2 R_j^2 d\rho=\frac{c^2}{2} J^2_{\nu+1}(\alpha_j c). \nonumber \]
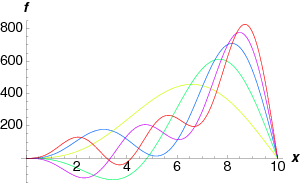
Consider the function
\[f(x) = \left\{\begin{array}{ll} x^3 &\;\;0<x<10\\ 0&\;\;x>10 \end{array}\right. \nonumber \]
Expand this function in a Fourier-Bessel series using \(J_3\).
Solution
From our definitions we find that
\[f(x) = \sum_{j=1}^\infty A_j J_3(\alpha_j x), \nonumber \]
with
\[\begin{aligned} A_j &= \frac{2}{100 J_4(10\alpha_j)^2} \int_0^{10} x^3 J_3(\alpha_j x) dx\nonumber\\ &=\frac{2}{100 J_4(10\alpha_j)^2} \frac{1}{\alpha^5_j} \int_0^{10\alpha_j} s^4 J_3(s) ds\nonumber\\ &=\frac{2}{100 J_4(10\alpha_j)^2} \frac{1}{\alpha^5_j} (10 \alpha_j)^4 J_4(10\alpha_j ) ds\nonumber\\ &= \frac{200}{\alpha_j J_4(10 \alpha_j)}.\end{aligned} \nonumber \]
Using \(\alpha_j=\ldots\), we find that the first five values of \(A_j\) are \(1050.95,-821.503,703.991,-627.577,572.301\). The first five partial sums are plotted in Fig. \(\PageIndex{1}\).