10.2: Bessel’s Equation
- Page ID
- 8332
Bessel’s equation of order \(\nu\) is given by \[x^2 y'' + x y' + (x^2-\nu^2) y = 0. \nonumber \] Clearly \(x=0\) is a regular singular point, so we can solve by Frobenius’ method. The indicial equation is obtained from the lowest power after the substitution \(y=x^\gamma\), and is
\[\gamma^2-\nu^2=0 \nonumber \]
So a generalized series solution gives two independent solutions if \(\nu \neq \frac{1}{2} n\). Now let us solve the problem and explicitly substitute the power series,
\[y = x^\nu \sum_n a_n x^n. \nonumber \]
From Bessel’s equation we find
\[\sum_n(n+\nu)(n+\nu-1) a_\nu x^{m+\nu} +\sum_n(n+\nu)a_\nu x^{m+\nu} +\sum_n(x^2-\nu^2)a_\nu = 0 \nonumber \]
which leads to
\[[(m+\nu)^2-\nu^2] a_m= -a_{m-2} \nonumber \] or \[a_m= -\frac{1}{m(m+2\nu)}a_{m-2}. \nonumber \]
If we take \(\nu=n>0\), we have
\[a_m= -\frac{1}{m(m+2n)}a_{m-2}. \nonumber \]
This can be solved by iteration,
\[\begin{aligned} a_{2k} &= -\frac{1}{4}\frac{1}{k(k+n)}a_{2(k-1)}\nonumber\\ &= \left(\frac{1}{4}\right)^2\frac{1}{k(k-1)(k+n)(k+n-1)}a_{2(k-2)} \nonumber\\ &= \left(-\frac{1}{4}\right)^k\frac{n!}{k!(k+n)!}a_{0}.\end{aligned} \nonumber \]
If we choose1 \(a_0 = \frac{1}{n!2^n}\) we find the Bessel function of order \(n\)
\[J_n(x) = \sum_{k=0}^\infty \frac{(-1)^k}{k!(k+n)!} \left(\frac{x}{2}\right)^{2k+n}. \nonumber \]
There is another second independent solution (which should have a logarithm in it) with goes to infinity at \(x=0\).
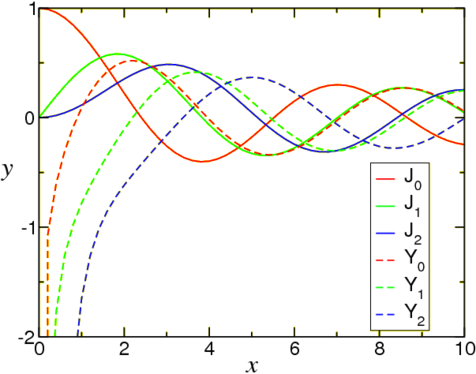
Figure \(\PageIndex{1}\): A plot of the first three Bessel functions \(J_n\) and \(Y_n\).
The general solution of Bessel’s equation of order \(n\) is a linear combination of \(J\) and \(Y\), \[y(x) = A J_n(x)+B Y_n(x). \nonumber \]
- This can be done since Bessel’s equation is linear, i.e., if \(g(x)\) is a solution \(C g(x)\) is also a solution.↩


