3.4: More Realistic Examples of Boundary and Initial Conditions
- Page ID
- 8358
A String with Fixed Endpoints
Consider a string fixed at \(x=0\) and \(x=a\), as in Figure \(\PageIndex{1}\)
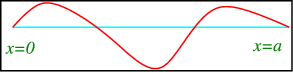
It satisfies the wave equation
\[\frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2},\space \space\space\qquad 0<x<a, \nonumber \]
with boundary conditions \[u(0,t) = u(a,t) = 0, \qquad t>0, \nonumber \]
and initial conditions,
\[u(x,0) = f(x), \frac{\partial u}{\partial x}(x,0) = g(x). \nonumber \]
A String with Freely Floating Endpoints
Consider a string with ends fastened to air bearings that are fixed to a rod orthogonal to the \(x\)-axis. Since the bearings float freely there should be no force along the rods, which means that the string is horizontal at the bearings (Figure \(\PageIndex{2}\)).
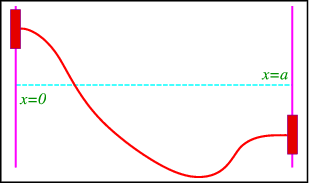
It satisfies the wave equation with the same initial conditions as above, but the boundary conditions now are \[\frac{\partial u}{\partial x} (0,t) = \frac{\partial u}{\partial x} (a,t) = 0, \space\space \qquad t>0. \nonumber \] These are clearly of von Neumann type.
A String with Endpoints Fixed to Strings
To illustrate mixed boundary conditions we make an even more complicated contraption where we fix the endpoints of the string to springs, with equilibrium at \(y=0\), see Figure \(\PageIndex{3}\) for a sketch.
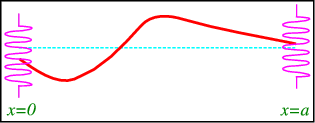
Hook’s law states that the force exerted by the spring (along the \(y\) axis) is \(F=-ku(0,t)\), where \(k\) is the spring constant. This must be balanced by the force the string on the spring, which is equal to the tension \(T\) in the string. The component parallel to the \(y\) axis is \(T\sin\alpha\), where \(\alpha\) is the angle with the horizontal, see Figure \(\PageIndex{4}\).
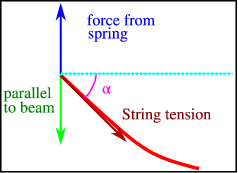
For small \(\alpha\) we have
\[\sin\alpha \approx \tan\alpha = \frac{\partial u}{\partial x}(0,t). \nonumber \]
Since both forces should cancel we find
\[ {u}(0,t) -\frac{T}{k} \frac{\partial u}{\partial x}(0,t) = 0, \qquad t>0, \nonumber \]
and
\[ u(a,t) -\frac{T}{k} \frac{\partial u}{\partial x}(a,t) = 0, \nonumber \]
These are mixed boundary conditions.


