5.6: Inhomogeneous Equations
- Page ID
- 8345
Consider a rod of length \(2\)m, laterally insulated (heat only flows inside the rod). Initially the temperature \(u\) is
\[\frac{1}{k}\sin\left( \frac{\pi x}{2} \right) + 500 \text{ K}. \nonumber \]
The left and right ends are both attached to a thermostat, and the temperature at the left side is fixed at a temperature of \(500\text{ K}\) and the right end at \(100\text{ K}\). There is also a heater attached to the rod that adds a constant heat of \(\sin\left( \frac{\pi x}{2}\right)\) to the rod. The differential equation describing this is inhomogeneous
\[\begin{aligned} \dfrac{\partial}{\partial t} u &= k \dfrac{\partial^2}{\partial x^2} u + \sin\left(\frac{\pi x}{2}\right),\nonumber\\[4pt] u(0,t) &= 500,\nonumber\\[4pt] u(2,t) &= 100,\nonumber\\[4pt] u(x,0) &= \frac{1}{k}\sin\left( \frac{\pi x}{2} \right) + 500.\end{aligned} \nonumber \]
ince the inhomogeneity is time-independent we write
\[u(x,t) = v(x,t) + h(x), \nonumber \]
where \(h\) will be determined so as to make \(v\) satisfy a homogeneous equation. Substituting this form, we find
\[\dfrac{\partial}{\partial t} v = k \dfrac{\partial^2}{\partial x^2} v + k h'' + \sin\left( \frac{\pi x}{2} \right). \nonumber \]
To make the equation for \(v\) homogeneous we require \[h''(x) = - \frac{1}{k}\sin\left( \frac{\pi x}{2} \right), \nonumber \]
which has the solution
\[h(x) = C_1 x + C_2 + \frac{4}{k\pi^2}\sin\left( \frac{\pi x}{2} \right). \nonumber \]
At the same time we let \(h\) carry the boundary conditions, \(h(0)=500\), \(h(2)=100\), and thus \[h(x) = -{200} x + 500 + \frac{4}{k\pi^2}\sin\left( \frac{\pi x}{2} \right). \nonumber \] The function \(v\) satisfies
\[\begin{aligned} \dfrac{\partial}{\partial t} v &= k \dfrac{\partial^2}{\partial x^2} v, \nonumber\\[4pt] v(0,t) & = v(\pi,t) = 0, \nonumber\\[4pt] v(x,0) & = u(x,0) - h(x) = {200} x.\end{aligned} \nonumber \]
This is a problem of a type that we have seen before. By separation of variables we find
\[v(x,t) = \sum_{n=1}^\infty b_n \exp (- \frac{n^2\pi^2}{4}kt) \sin \frac{n\pi}{2}x. \nonumber \]
The initial condition gives
\[\sum_{n=1}^\infty b_n \sin nx = {200} x. \nonumber \]
from which we find
\[b_n = (-1)^{n+1} \frac{800}{n\pi}. \nonumber \]
And thus
\[u(x,t) = -\frac{200} x + 500 + \frac{4}{\pi^2 k} \sin \left(\frac{\pi x}{2}\right) + \frac{800}{\pi} \sum_{n=1}^\infty \frac{(-1)^n}{n+1} \sin \left(\frac{\pi nx}{2}\right) e^{-k (n \pi/2)^2 t}. \label{eq.10} \]
Note: as \(t\rightarrow \infty\), \(u(x,t) \rightarrow -\frac{400}{\pi} x + 500 + \frac{\sin \frac{\pi}{2}x}{k}\). As can be seen in Fig. \(\PageIndex{1}\) this approach is quite rapid – we have chosen \(k=1/500\) in that figure, and summed over the first 60 solutions.
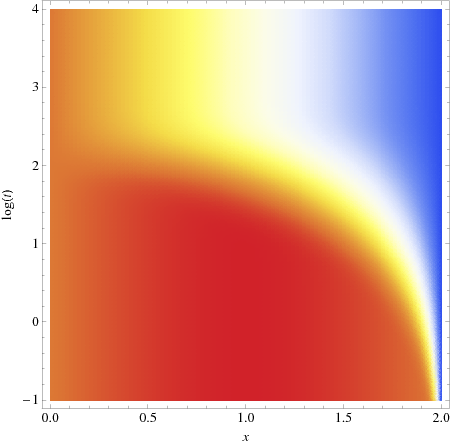
Figure \(\PageIndex{1}\): Time dependence of the solution to the inhomogeneous Equation \ref{eq.10}.


