7.5: Parallelograms

Last updated
Save as PDF

Page ID: 23623

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

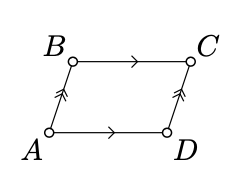
$截屏2021-02-11 上午10.56.21.png$

A quadrangle $ABCD$ in the Euclidean plane is called nondegenerate if no three points from $A, B, C, D$ lie on one line.

A nondegenerate quadrangle is called a parallelogram if its opposite sides are parallel.

Lemma $\PageIndex{1}$

Any parallelogram is centrally symmetric with respect to a midpoint of one of its diagolals.

In particular, if $\square ABCD$ is a parallelogram, then

(a) its diagonals $[AC]$ and $[BD]$ intersect each other at their midpoints;

(b) $\measuredangle ABC = \measuredangle CDA$;

Proof

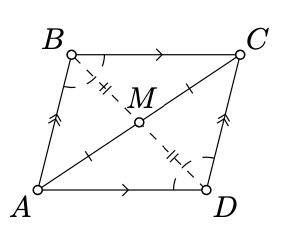
$截屏2021-02-11 上午10.59.25.png$

Let $\square ABCD$ be a parallelogram. Denote by $M$ the midpoint of $[AC]$.

Since $(AB)\parallel (CD)$, Theorem 7.2.1 implies that $(CD)$ is a reflection of $(AB)$ across $M$. The same way $(BC)$ is a reflection of $(DA)$ across $M$. Since $\square ABCD$ is nondegenerate, it follows that $D$ is a reflection of $B$ across $M$; in other words, $M$ is the midpoint of $[BD]$.

The remaining statements follow since reflection across $M$ is a direct motion of the plane (see Proposition 7.2.1).

Exercise $\PageIndex{1}$

Assume $ABCD$ is a quadrangle such that

$AB = CD = BC = DA.$

Such that $ABCD$ is a parallelogram.

Hint

Since $\triangle ABC$ is isosceles, $\measuredangle CAB = \measuredangle BCA$.

By SSS, $\triangle ABC \cong \triangle CDA$. Therefore, $\pm \measuredangle DCA = \measuredangle BCA = \measuredangle CAB$.

Since $D \ne C$, we get "-" in the last formula. Use the transversal property (Theorem 7.3.1) to show that $(AB) \parallel (CD)$. Repeat the argument to show that $(AD) \parallel (BC)$.

A quadrangle as in the exercise above is called a rhombus.

A quadrangle ABCD is called a rectangle if the angles ABC, BCD, CDA, and DAB are right. Note that according to the transversal property (Theorem 7.3.1), any rectangle is a parallelogram.

A rectangle with equal sides is called a square.

Exercise $\PageIndex{2}$

Show that the parallelogram $ABCD$ is a rectangle if and only if $AC = BD$.

Hint

By Lemma $\PageIndex{1}$ and SSS, $AC = BD$ if and only if $\angle ABC = \pm \measuredangle BCD$. By the transversal property (Theorem 7.3.1), $\measuredangle ABC + \measuredangle BCD \equiv \pi$.

Therefore, $AC = BD$ if and only if $\measuredangle ABC = \measuredangle BCD = \pm \dfrac{\pi}{2}$.

Exercise $\PageIndex{3}$

Show that the parallelogram $ABCD$ is a rhombus if and only if $(AC) \perp (BD)$.

Hint

Fix a parallelogram $ABCD$. By Lemma $\PageIndex{1}$, its diagonals $[AC]$ and $[BD]$ have a common midpoint; denote it by $M$.

Use SSS and Lemma $\PageIndex{1}$ to show that

$AB = CD \Leftrightarrow \triangle AMB \cong \triangle AMD \Leftrightarrow \measuredangle AMB = \pm \dfrac{\pi}{2}.$

Assume $\ell \parallel m$, and $X, Y \in m$. Let $X'$ and $Y'$ denote the foot points of $X$ and $Y$ on $\ell$. Note that $\square XYY'X'$ is a rectangle. By Lemma $\PageIndex{1}$, $XX' = YY'$. That is, any point on $m$ lies on the same distance from $\ell$. This distance is called the distance between $\ell$ and $m$.

Lemma \(\PageIndex{1}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)