1.5: Isometries, motions, and lines
- Page ID
- 23581
In this section, we define lines in a metric space. Once it is done the sentence “We can draw a unique line that passes thru two given points.” becomes rigorous; see (ii) in Section 1.1.
Recall that a map \(f: \mathcal{X} \to \mathcal{Y}\) is a bijection, if it gives an exact pairing of the elements of two sets. Equivalently, \(f: \mathcal{X} \to \mathcal{Y}\) is a bijection, if it has an inverse; that is, a map \(g: \mathcal{Y} \to \mathcal{X}\) such that \(g(f(A)) = A\) for any \(A \in \mathcal{X}\) and \(f(g(B)) = B\) for any \(B \in \mathcal{Y}\).
Let \(\mathcal{X}\) and \(\mathcal{Y}\) be two metric spaces and \(d_{\mathcal{X}}\), \(d_{\mathcal{Y}}\) be their metrics. A map
\[f: \mathcal{X} \to \mathcal{Y}\]
is called distance-preserving if
\[d_{\mathcal{Y}} (f(A), f(B)) = d_{\mathcal{X}} (A, B)\]
for any \(A, B \in \mathcal{X}\).
A bijective distance-preserving map is called an isometry.
Two metric spaces are called isometric if there exists an isometry from one to the other.
The isometry from a metric space to itself is also called a motion of the space.
Exercise \(\PageIndex{1}\)
Show that any distance-preserving map is injective; that is, if \(f: \mathcal{X} \to \mathcal{Y}\) is a distance-preserving map, then \(f(A) \ne f(B)\) for any pair of distinct points \(A, B \in \mathcal{X}\).
- Hint
-
If \(A \ne B\), then \(d_{\mathcal{X} (A, B) > 0\). Since \(f\) is distance-preserving,
\(d_{\mathcal{Y}} (f(A), f(B)) = d_{\mathcal{X}} (A, B)\).
Therefore, \(d_{\mathcal{Y}} (f(A), f(B)) > 0\); hence \(f(A) \ne f(B)\).
Exercise \(\PageIndex{2}\)
Show that if \(f: \mathbb{R} \to \mathbb{R}\) is a motion of the real line, then either
(a) \(f(x) = f(0) + x\) for any \(x \in \mathbb{R}\), or
(b) \(f(x) = f(0) - x\) for any \(x \in \mathbb{R}\).
- Hint
-
Set \(f(0) = a\) and \(f(1) = b\). Note that \(b = a + 1\) or \(a - 1\). Moreover, \(f(x) = a \pm x\) and at the same time, \(f(x) = b \pm (x - 1)\) for any \(x\).
If \(b = a + 1\), it follows that \(f(x) = a + x\) for any \(x\).
The same way, if \(b = a - 1\), it follows that \(f(x) = a - x\) for any \(x\).
Exercise \(\PageIndex{3}\)
Prove that \((\mathbb{R}^2, d_1)\) is isometric to \((\mathbb{R}^2, d_{\infty})\).
- Hint
-
Show that the map \((x, y) \mapsto (x + y, x - y)\) is an isometry \((\mathbb{R}^2, d_1) \to (\mathbb{R}^2, d_{\infty})\). That is, you need to check if this map is bijective and distance-preserving.
Advanced Exercise \(\PageIndex{4}\)
Describe all the motions of the Manhattan plane, defined in Section 1.4.
- Hint
-
First prove that two points \(A = (x_A, y_A)\) and \(B = (x_B, y_B)\) on the Manhattan plane have a unique midpoint if and only if \(x_A = x_B\) or \(y_A = y_B\); compare with the example in Congruent triangles.
Then use above statement to prove that any motion of the Manhattan plane can be written in one of the following two ways:
\((x, y) \mapsto (\pm x + a, \pm y + b)\) or \((x, y) \mapsto (\pm y + b, \pm x + a)\),
for some fixed real numbers \(a\) and \(b\). (In each case we have 4 choices of signs, so for a fixed pair \((a, b)\) we have 8 distinct motions.)
If \(\mathcal{X}\) is a metric space and \(\mathcal{Y}\) is a subset of \(\mathcal{X}\), then a metric on \(\mathcal{Y}\) can be obtained by restricting the metric from \(\mathcal{X}\). In other words, the distance between two points of \(\mathcal{Y}\) is defined to be the distance between these points in \(\mathcal{X}\). This way any subset of a metric space can be also considered as a metric space.
A subset \(l\) of metric space is called a line, if it is isometric to the real line.
A triple of points that lie on one line is called collinear. Note that if \(A\), \(B\), and \(C\) are collinear, \(AC \ge AB\) and \(AC \ge BC\), then \(AC = AB + BC\).
Some metric spaces have no lines, for example discrete metrics. The picture shows examples of lines on the Manhattan plane \((\mathbb{R}^2, d_1)\).
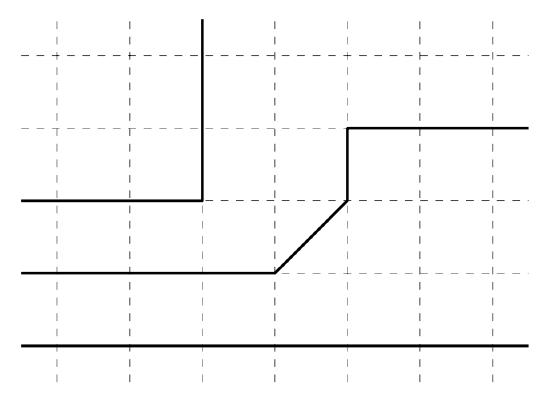
Exercise \(\PageIndex{5}\)
Consider the graph \(y = |x|\) in \(\mathbb{R}^2\). In which of the following spaces (a) \((\mathbb{R}^2, d_1)\), (b) \((\mathbb{R}^2, d_2)\), (c) \((\mathbb{R}^2, d_{\infty})\) does it form a line? Why?
- Hint
-
Assume three points \(A, B\), and \(C\) lie on one line, Note that in this case one of the triangle inequalities with the points \(A, B\), and \(C\) becomes an equality.
Set \(A = (-1, 1)\), \(B = (0, 0)\), and \(C = (1, 1)\). Show that for \(d_1\) and \(d_2\) all the triangle inequalities with the points \(A, B\), and \(C\) are strict. It follows that the graph is not a line.
For \(d_{\infty}\) show that \((x, |x|) \mapsto x\) gives the isometry of the graph to \(\mathbb{R}\). Conclude that the graph is a line in \((\mathbb{R}^2, d_{\infty})\).
Exercise \(\PageIndex{6}\)
Show that any motion maps a line to a line.
- Hint
-
Spell the definitions of line and motion.


