3.5: Triangle with the given sides
- Page ID
- 23595
Consider the triangle \(ABC\). Set
\(a = BC\), \(b = CA\), \(c = AB.\)
Without loss of generality, we may assume that
\(a \le b \le c.\)
Then all three triangle inequalities for \(\triangle ABC\) hold if and only if
\(c \le a + b\).
The following theorem states that this is the only restriction on \(a\), \(b\), and \(c\).
Assume that \(0 < a \le b \le c \le a + b\). Then there is a triangle with sides \(a, b\), and \(c\); that is, there is \(\triangle ABC\) such that \(a = BC\), \(b = CA\), and \(c = AB\).
- Proof
-
Fix the points \(A\) and \(B\) such that \(AB = c\). Given \(\beta \in [0, \pi]\), suppose that \(C_{\beta}\) denotes the point in the plane such that \(BC_{\beta} = a\) and \(\measuredangle ABC = \beta\).
According the Corollary \(\PageIndex{1}\), the map \(\beta \mapsto C_{\beta}\) is continuous. Therefore, the function \(b(\beta) = AC_{\beta}\)is continous (formally, it follows from Exercise 1.9.1 and Exercise 1.9.2).
Note that \(b(0) = c - a\) and \(b (\pi) = c + a\). Since \(c - a \le b \le c + a\), by the intermediate value theorem (Theorem 3.2.1) there is \(\beta_0 \in [0, \pi]\) such that \(b(\beta_0) = b\), hence the result.
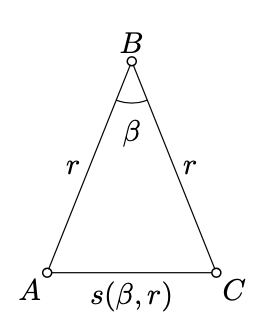
Assume \(r > 0\) and \(\pi > \beta > 0\). Consider the triangle \(ABC\) such that \(AB = BC = r\) and \(\measuredangle ABC = \beta\). The existence of such a triangle follows from Axiom IIIa and Proposition 2.2.2.
Note that according to Axiom IV, the values \(\beta\) and \(r\) define the triangle \(ABC\) up to the congruence. In particular, the distance \(AC\) depends only on \(\beta\) and \(r\).
\[s(\beta, r):= AC.\]
Given \(r > 0\) and \(\varepsilon > 0\), there is \(\delta > 0\) such that
\(0 < \beta < \delta \Rightarrow s(r, \beta) < \varepsilon.\)
- Proof
-
Fix two points \(A\) and \(B\) such that \(AB = r\).
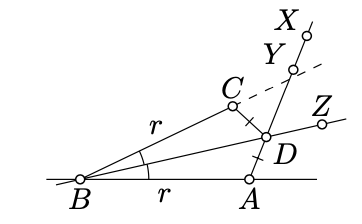
Choose a point \(X\) such that \(AY = \dfrac{\varepsilon}{2}\); it exists by Proposition 2.2.2.
Note that \(X\) and \(Y\) lie on the same side of \((AB)\); therefore, \(\angle ABY\) is positive. Set \(\delta = \measuredangle ABY\).
Suppose \(0 < \beta < \delta\); by Axiom IIIa, we can choose \(B\) so that \(\measuredangle ABC = \beta\) and \(BC = r\). Further we can choose a half-line \([BZ)\) such that \(\measuredangle ABZ = \dfrac{1}{2} \cdot \beta\).
Note that \(A\) and \(Y\) lie on opposite sides of \((BZ)\) and moreover \(\measuredangle ABZ \equiv - \measuredangle CBZ\). In particular, \((BZ)\) intersects \([AY]\); denote by \(D\) the point of intersection.
Since \(D\) lies between \(A\) and \(Y\), we have that \(AD < AY\).
Since \(D\) lies on \((BZ)\) we have that \(\measuredangle ABD \equiv \measuredangle CBD\). By Axiom IV, \(\triangle ABD \cong \triangle CBD\). It follows that
\[\begin{array} {rcl} {s(r, \beta)} & = & {AC \le} \\ {} & \le & {AD + DC =} \\ {} & = & {2 \cdot AD <} \\ {} & < & {2 \cdot AY =} \\ {} & = & {\varepsilon} \end{array}\]
Fix a real number \(r > 0\) and two distinct points \(A\) and \(B\). Then for any real number \(\beta \in [0, \pi]\), there is a unique point \(C_{\beta}\) such that \(BC_{\beta} = r\) and \(\measuredangle ABC_{\beta} = \beta\). Moreover, \(\beta \mapsto C_{\beta}\) is a continuous map from \([0, \pi]\) to the plane.
- Proof
-
The existence and uniqueness of \(C_{\beta}\) follows from Axiom IIIa and Proposition 2.2.2.
Note taht if \(\beta_1 \ne \beta_2\), then
\[C_{\beta_1} C_{\beta_2} = s(r, |\beta_1 - \beta_2|).\]
By Proposition \(\PageIndex{1}\), the map \(\beta \mapsto C_{\beta}\) is continuous.
Given a positive real number \(r\) and a pint \(O\), the set \(\Gamma\) of all points on distance \(r\) from \(O\) is called a circle with radius \(r\) and center \(O\).
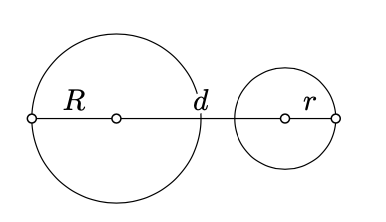
Exercise \(\PageIndex{1}\)
Show that two circles intersect if and only if
\[|R - r| \le d \le R + r,\]
where \(R\) and \(r\) denote their radiuses, and \(d\) — the distance between their centers.
- Hint
-
The "only-if" part follows from the triangle inequality. To prove "if" part, observe that Theorem \(\PageIndex{1}\) implies existence of a triangle with sides \(r_1\), \(r_2\), and \(d\). Use this triangle to show that there is a point \(X\) such that \(O_1X = r_1\) and \(O_2X = r_2\), where \(O_1\) and \(O_2\) are the centers of the corresponding circles.


