4.2: Angle-Side-Angle Condition

Last updated
Save as PDF

Page ID: 23599

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Theorem $\PageIndex{1}$ ASA condition

Assume that

$AB = A'B'$, $\measuredangle ABC = \pm \measuredangle A'B'C'$, $\measuredangle CAB = \pm \measuredangle C'A'B'$

and $\triangle A'B'C'$ is nondegenerate. Then

$\triangle ABC \cong \triangle A'B'C'$.

Note that for degenerate triangles the statement does not hold. For example, consider one triangle with sides 1, 4, 5 and the other with sides 2, 3, 5.

Proof

According to Theorem 3.3.1, either

\[\begin{array} {l} {\meausredangle ABC = \measuredangle A'B'C',} \\ {\measuredangle CAB = \measuredangle C'A'B'} \end{array}\]

\[\begin{array} {l} {\meausredangle ABC = -\measuredangle A'B'C',} \\ {\measuredangle CAB = -\measuredangle C'A'B'.} \end{array}\]

Further we assume that 4.2.1 holds; the case 4.2.2 is analogous.

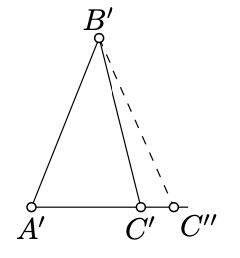
$截屏2021-02-03 上午10.47.15.png$

Let $C''$ be the point on the half-line $[A'C')$ such that $A'C'' = AC$.

By Axiom IV, $\triangle A'B'C'' \cong \triangle ABC$. Applying Axiom IV again, we get that

$\measuredangle A'B'C'' = \measuredangle ABC = \measuredangle A'B'C'$.

By Axiom IIIa, $[B'C') = [BC'')$. Hence $C''$ lies on $(B'C')$ as well as on $(A'C')$.

Since $\triangle A'B'C'$ is not degenerate, $(A'C')$ is distinct from $(B'C')$. Applying Axiom II, we get that $C'' = C'$.

Therefore, $\triangle A'B'C' = \triangle A'B'C'' \cong \triangle ABC$.