5.7: Geometric constructions
- Page ID
- 57059
The ruler-and-compass constructions in the plane is the construction of points, lines, and circles using only an idealized ruler and compass. These construction problems provide a valuable source of exercises in geometry, which we will use further in the book. In addition, Chapter 19 is devoted completely to the subject.
The idealized ruler can be used only to draw a line thru the given two points. The idealized compass can be used only to draw a circle with a given center and radius. That is, given three points \(A, B\), and \(O\) we can draw the set of all points on distance \(AB\) from \(O\). We may also mark new points in the plane as well as on the constructed lines, circles and their intersections (assuming that such points exist).
We can also look at the different sets of construction tools. For example, we may only use the ruler or we may invent a new tool, say a tool that produces a midpoint for any given two points.
As an example, let us consider the following problem:
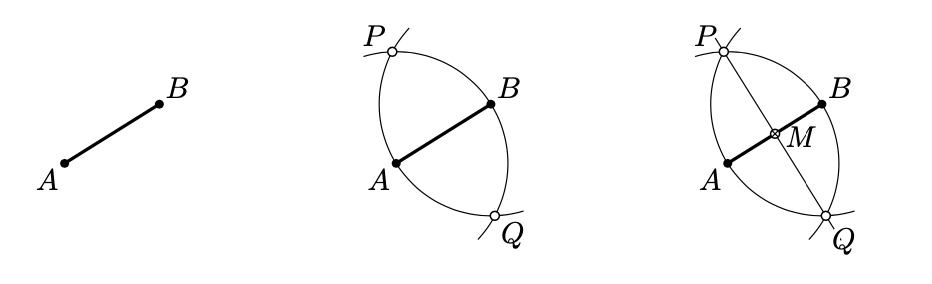
Construct the midpoint of the given segment \([AB]\).
Construction.
- Construct the circle with center at \(A\) that is passing thru \(B\). Construct the circle with center at \(B\) that is passing thru \(A\). Mark both points of intersection of these circles, label them with \(P\) and \(Q\).
- Draw the line \((PQ)\). Mark the point \(M\) of intersection of \((PQ)\) and \([AB]\); this is the midpoint.
Typically, you need to prove that the construction produces what was expected. Here is a proof for the example above.
- Proof
-
According the Theorem 5.2.1, \((PQ)\) is the perpendicular bisector to \([AB]\). Therefore, \(M = (AB) \cap (PQ)\) is the midpoint of \([AB]\).
Make a ruler-and-compass construction of a line thru a given point that is perpendicular to a given line.
- Hint
-
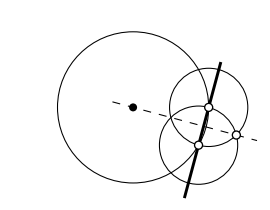
Make a ruler-and-compass construction of the center of a given circle.
- Hint
-
Make a ruler-and-compass construction of the lines tan- gent to a given circle that pass thru a given point.
- Hint
-
Given two circles \(\Gamma_1\) and \(\Gamma_2\) and a segment \([AB]\) make a ruler-and-compass construction of a circle with the radius \(AB\) that is tangent to each circle \(\Gamma_1\) and \(\Gamma_2\).
- Hint
-