6.4: Ptolemy's inequality
- Page ID
- 23615
A quadrangle is defined as an ordered quadruple of distinct points in the plane. These 4 points are called vertexes of quadrangle. The quadrangle ABCD will be also denoted by \(\square ABCD\).
Given a quadrangle \(ABCD\), the four segments \([AB]\), \([BC]\), \([CD]\), and \([DA]\) are called sides of \(\square ABCD\); the remaining two segments \([AC]\) and \([BD]\) are called diagonals of \(\square ABCD\).
In any quadrangle, the product of diagonals cannot exceed the sum of the products of its opposite sides; that is,
\[AC \cdot BD \le AB \cdot CD + BC \cdot DA\]
for any \(\square ABCD\).
We will present a classical proof of this inequality using the method of similar triangles with an additional construction. This proof is given as an illustration — it will not be used further in the sequel.
- Proof
-
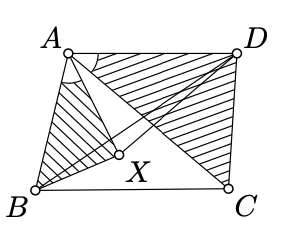
Consider the half-line \([AX)\) such that \(\measuredangle BAX = \measuredangle CAD\). In this case \(\measuredangle XAD = \measuredangle BAC\) since adding \(\measuredangle BAX\) or \(\measuredangle CAD\) to the corresponding sides produces \(\measuredangle BAD\). We can assume that
\(AX = \dfrac{AB}{AC} \cdot AD.\)
In this case we have
\(\dfrac{AX}{AD} = \dfrac{AB}{AC}\), \(\dfrac{AX}{AB} = \dfrac{AD}{AC}.\)
Hence
\(\triangle BAX \sim \triangle CAD\), \(\triangle XAD \sim \triangle BAC\).
Therefore,
\(\dfrac{BX}{CD} = \dfrac{AB}{AC}\), \(\dfrac{XD}{BC} = \dfrac{AD}{AC}.\)
or, equivalently
\(AC \cdot BX = AB \cdot CD\), \(AC \cdot XD = BC \cdot AD\).
Adding these two equalities we get
\(AC \cdot (BX + XD) = AB \cdot CD + BC \cdot AD\).
It remains to apply the triangle inequality, \(BD \le BX + XD\).
Using the proof above together with Corollary 9.3.2, one can show that the equality holds only if the vertexes \(A, B, C\), and \(D\) appear on a line or a circle in the same cyclic order; see also Theorem 10.4.1 for another proof of the equality case. Exercise 18.3.2 below suggests another proof of Ptolemy’s inequality using complex coordinates.


