7.4: Angles of triangles
- Page ID
- 23622
In any \(\triangle ABC\), we have
\(\measuredangle ABC + \measuredangle BCA + \measuredangle CAB \equiv \pi.\)
- Proof
-
First note that if \(\triangle ABC\) is degenerate, then the equality follows from Corollary 2.4.1. Further we assume that \(\triangle ABC\) is nondegenerate.
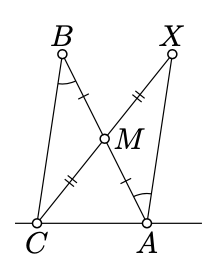
Let \(X\) be the reflection of \(C\) across the the midpoint \(M\) of \([AB]\). By Proposition 7.2.1 \(\measuredangle BAX = \measuredangle ABC\). Note that \((AX)\) is a reflection of \((CB)\) across \(M\); therefore by Theorem 7.2.1, \((AX) \parallel (CB)\).
Since \([BM]\) and \([MX]\) do not intersect \((CA)\), the points \(B, M\), and \(X\) lie on the same side of \((CA)\). Applying the transversal property for the transversal \((CA)\) to \((AX)\) and \((CB)\), we get that
\[\measuredangle BCA + \measuredangle CAX \equiv \pi.\]
Since \(\measuredangle BAX = \measuredangle ABC\), we have
\(\measuredangle CAX \equiv \measuredangle CAB + \measuredangle ABC\)
The latter identity and 7.4.1 imply the theorem.
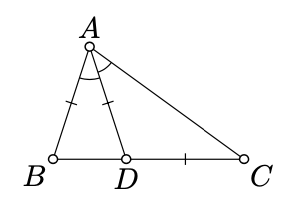
Let \(\triangle ABC\) be a nondegenerate triangle. Assume there is a point \(D \in [BC]\) such that
\(\measuredangle BAD \equiv \measuredangle DAC, BA = AD = DC.\)
Find the angles of \(\triangle ABC\).
- Hint
-
Apply twice Theorem 4.3.1 and twice Theorem \(\PageIndex{1}\).
Show that
\(|\measuredangle ABC| + |\measuredangle BCA| + |\measuredangle CAB| = \pi\)
for any \(\triangle ABC\).
- Hint
-
If \(\triangle ABC\) is degenerate, then one of the angle measures is \(\pi\) and the other two are 0. Hence the result.
Assume \(\triangle ABC\) is nondegenerate. Set \(\alpha = \measuredangle CAB\), \(\beta = \measuredangle ABC\), and \(\gamma = \measuredangle BCA\).
By Theorem 3.3.1, we may assume that \(0 < \alpha, \beta, \gamma < \pi\). Therefore,
\[0 > \alpha + \beta + \gamma < 3 \cdot \pi.\]
By Theorem \(\Pageindex{1}\),
\[\alpha + \beta +\gamma \equiv \pi.\]
From 7.4.2 and 7.4.3 the result follows.
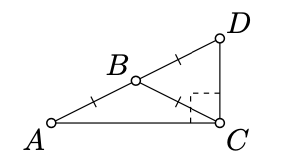
Let \(\triangle ABC\) be an isoseles nondegenerate triangle with the base \([AC]\). Suppose \(D\) is a reflection of \(A\) across \(B\). Show that \(\angle ACD\) is right.
- Hint
-
Apply twice Theorem 4.3.1 and twice Theorem \(\PageIndex{1}\).
Let \(\triangle ABC\) be an isosceles nondegenerate triangel with base \([AC]\). Assume that a circle is passing thru \(A\), centered at a point on \([AB]\), and tangent to \((BC)\) at the point \(X\). Show that \(\measuredangle CAX = \pm \dfrac{\pi}{4}\).
- Hint
-
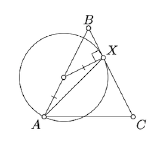
Suppose that \(O\) denotes the center of the circle.
Note that \(\triangle AOX\) is isosceles and \(\angle OXC\) is right. Applying Theorem \(\PageIndex{1}\) and Theorem 4.3.1 and simplifying, we should get \(4 \cdot \measuredangle CAX \equiv \pi\).
Show that \(\angle CAX\) has to be acute. It follows then that \(\measuredangle CAX = \pm \dfrac{\pi}{4}\).
Show that for any quadrangle \(ABCD\), we have
\(\measuredangle ABC + \measuredangle BCD + \measuredangle CDA + \measuredangle DAB \equiv 0\).
- Hint
-
Apply Theorem \(\PageIndex{1}\) to \(\triangle ABC\) and \(\triangle BDA\).


