7.7: Apollonian Circle

Last updated
Save as PDF

Page ID: 57420

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The exercises in this section are given as illustrations to the method of coordinates — it will not be used further in the sequel.

Exercise $\PageIndex{1}$

Show that for fixed real values $a$, $b$, and $c$ the equation

$x^2 + y^2 + a \cdot x + b \cdot y + c = 0$

describes a circle, one-point set or empty set.

Show that if it is a circle then it has center $(- \dfrac{a}{2}, -\dfrac{b}{2})$ and the radius $r = \dfrac{1}{2} \cdot \sqrt{a^2 + b^2 - 4 \cdot c}$.

Hint

Rewrite it the following way and think

$(x + \dfrac{a}{2})^2 + (y + \dfrac{b}{2})^2 = (\dfrac{a}{2})^2 + (\dfrac{b}{2})^2 - c$.

Exercise $\PageIndex{2}$

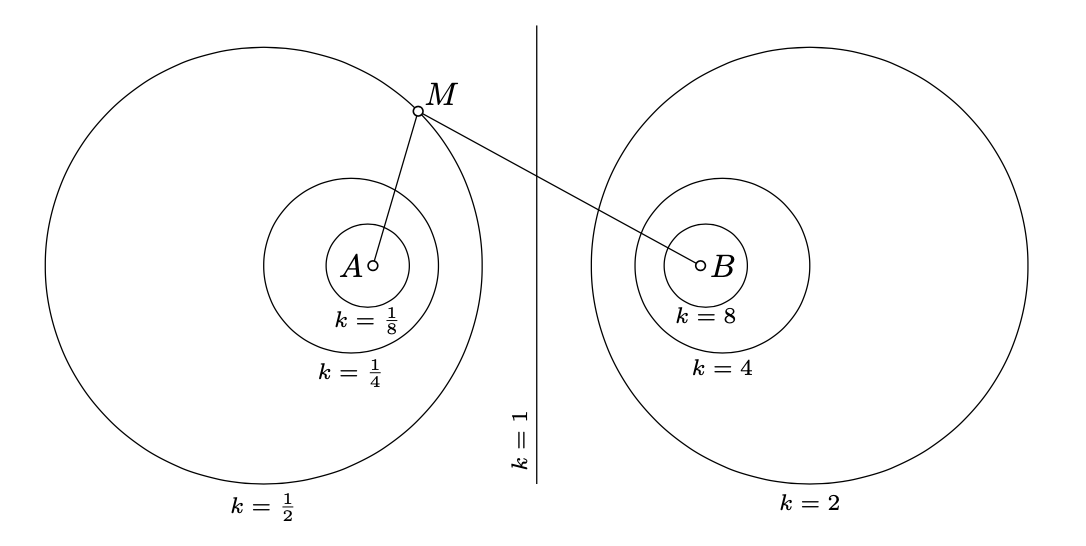
Use the previous exercise to show that given two distinct point $A$ and $B$ and positive real number $k \ne 1$, the locus of points $M$ such that $AM = k \cdot BM$ is a circle.

$截屏2021-02-15 下午2.34.40.png$

Hint

We can choose the coordinates so that $B = (0, 0)$ and $A = (a, 0)$ for some $a > 0$. If $M = (x, y)$, then the equation $AM = k \cdot BM$ can be written in coordinates as

$k^2 \cdot (x^2 + y^2) = (x - a)^2 + y^2.$

It remains to rewrite this equation as in Exercise $\PageIndex{1}$.

The circle in the exercise above is an example of the so-called Apollonian circle with focuses $A$ and $B$. Few of these circles for different values $k$ are shown on the diagram; for $k = 1$, it becomes the perpendicular bisector to $[AB]$.

Exercise $\PageIndex{3}$

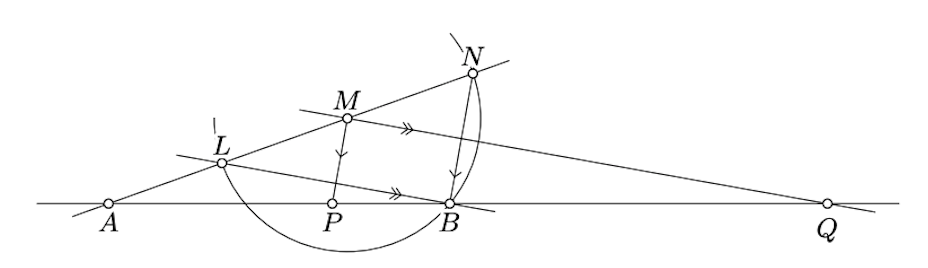
Make a ruler-and-compass construction of an Apollonian circle with given focuses $A$ and $B$ thru a given point $M$.

Hint

Assume $M \not\in (AB)$. Show and use that the points $P$ and $Q$ constructed on the following diagram lie on the the Apollonian circle.

$截屏2021-02-15 下午2.40.19.png$

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)