8.2: Altitudes and orthocenter

Last updated
Save as PDF

Page ID: 23627

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

An altitude of a triangle is a line thru a vertex and perpendicular to the line containing the opposite side. The term altitude may also be used for the distance from the vertex to its foot point on the line containing the opposite side.

Theorem $\PageIndex{1}$

The three altitudes of any nondegenerate triangle intersect in a single point.

The point of intersection of altitudes is called orthocenter; it is usually denoted by $H$.

Proof

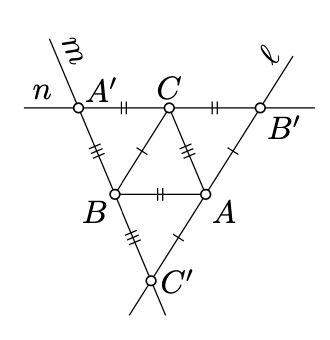
$截屏2021-02-15 下午3.08.46.png$

Fix a nondegenerate triangle $ABC$. Consider three lines $\ell, m$, and $n$ such that

$\begin{array} {ccccc} {\ell \parallel (BC),} & \ \ & {m \parallel (CA),} & \ \ & {n \parallel (AB),} \\ {\ell \ni A,} & \ \ & {m \ni B,} & \ \ & {n \ni C.} \end{array}$

Since $\triangle ABC$ is nondegenerate, no pair of the lines $\ell$, $m$, and $n$ is parallel. Set

$A' = m \cap n,$ $B' = n \cap \ell$, $C' = \ell \cap m$.

Note that $\square ABA'C$, $\square BCB'A$, and $\square CBC'A$ are parallelograms. Applying Lemma 7.5.1 we get that $\triangle ABC$ is the median triangle of $\triangle A'B'C'$; that is, $A$, $B$ and $C$ are the midpoints of $[B'C']$, $[C'A']$, and $[A'B']$ respectively.

By Exercise 7.1.1, $(B'C') \parallel (BC)$, the altitude from $A$ is perpendicular to $[B'C']$ and from above it bisects $[B'C']$. Hence the altitudes of $\triangle ABC$ are also perpendicular bisectors of $\triangle A'B'C'$. Applying Theorem 8.1.1, we get that altitudes of $\triangle ABC$ intersect at one point.

Exercise $\PageIndex{1}$

Assume $H$ is the orthocenter of an acute triangle $ABC$. Show that $A$ is the orthocenter of $\triangle HBC$.

Hint

Note that $(AC) \perp (BH)$ and $(BC) \perp (AH)$ and apply Theorem $\PageIndex{1}$

(Note that each of $A, B, C, H$ is the orthocenter of the remaining three; such a quadruple of points $A, B, C, H$ is called orthocentric system.