8.4: Angle Bisectors
- Page ID
- 23629
If \(\measuredangle ABX \equiv - \measuredangle CBX\), then we say that the line \((BX)\) bisects \(\angle ABC\), or the line \((BX)\) is a bisector of \(\angle ABC\). If \(\measuredangle ABX \equiv \pi - \measuredangle CBX\), then the line \((BX)\) is called the external bisector of \(\angle ABC\).
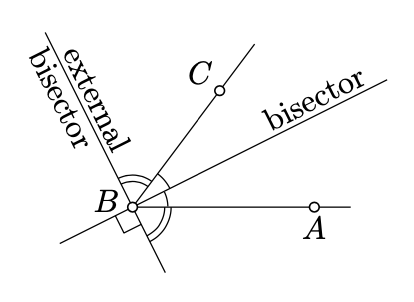
If \(\measuredangle ABA' = \pi\); that is, if \(B\) lies between \(A\) and \(A'\), then the bisector of \(\angle ABC\) is the external bisector of \(\angle A'BC\) and the other way around.
Note that the bisector and the external bisector are uniquely defined by the angle.
Show that for any angle, its bisector and external bisector are perpendicular.
- Hint
-
Let \((BX)\) and \((BY)\) be the internal and external bisectors of \(\angle ABC\). Then
\(2 \cdot \measuredangle XBY \equiv 2 \cdot \measuredangle XBA + 2 \cdot \measuredangle ABY \equiv \measuredangle CBA + \pi + 2 \cdot \measuredangle ABC \equiv \pi + \measuredangle CBC = \pi\)
and hence the result.
The bisectors of \(\angle ABC\), \(\angle BCA\), and \(\angle CAB\) of a nondegenerate triangle \(ABC\) are called bisectors of the triangle \(ABC\) at vertexes \(A, B\), and \(C\) respectively.
Let \(\triangle ABC\) be a nondegenerate triangle. Assume that the bisector at the vertex \(A\) intersects the side \([BC]\) at the point \(D\). Then
\[\dfrac{AB}{AC} = \dfrac{DB}{DC}.\]
- Proof
-
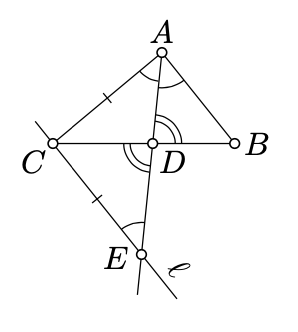
Let \(\ell\) be a line passing thru \(C\) that is parallel to \((AB)\). Note that \(\ell \nparallel (AD)\); set
\(E = \ell \cap (AD)\).
Also note that \(B\) and \(C\) lie on opposite sides of \((AD)\). Therefore, by the transversal property (Theorem 7.3.1),
\[\measuredangle BAD = \measuredangle CED.\]
Further, the angles \(ADB\) and \(EDC\) are vertical; in particular, by Proposition 2.5.1
\(\measuredangle ADB = \measuredangle EDC.\)
By the AA similarity condition, \(\triangle ABD \sim \triangle ECD\). In particular,
\[\dfrac{AB}{EC} = \dfrac{DB}{DC}.\]
Since \((AD)\) bisects \(\angle BAC\), we get that \(\measuredangle BAD = \measuredangle DAC\). Together with 8.4.2, it implies that \(\measuredangle CEA = \measuredangle EAC\). By Theorem 4.3.1, \(\triangle ACE\) is isosceles; that is,
\(EC = AC.\)
Together with 8.4.3, it implies 8.4.1.
Formulate and prove an analog of Lemma \(\PageIndex{1}\) for the external bisector.
- Hint
-
If \(E\) is the point of intersection of \((BC)\) with the external bisector of \(\angle BAC\), then \(\dfrac{AB}{AC} = \dfrac{EB}{EC}\). It can be proved along the same lines as Lemma \(\PageIndex{1}\).


