9.3: Points on a common circle
- Page ID
- 23635
Recall that the diameter of a circle is a chord that passes thru the center. If \([XY]\) is the diameter of a circle with center \(O\), then \(\measuredangle XOY = \pi\). Hence Theorem 9.2.1 implies the following:
Suppose \(\Gamma\) is a circle with the diameter \([AB]\). A triangle \(ABC\) has right angle at \(C\) if and only if \(C \in \Gamma\).
Given four points \(A, B, A'\), and \(B'\), construct a point \(Z\) such that both angles \(AZB\) and \(A'ZB'\) are right.
- Hint
-
Construct the circles \(\Gamma\) and \(\Gamma'\) on the diameters \([AB]\) and \([A'B']\) respectively. By Corollary \(\PageIndex{1}\), any point \(Z\) in the intersection \(\Gamma \cap \Gamma'\) will do.
Let \(\triangle ABC\) be a nondegenerate triangle, \(A'\) and \(B'\) be foot points of altitudes from \(A\) and \(B\) respectfully. Show that the four points \(A, B, A'\), and \(B'\) lie on one circle. What is the center of this circle?
- Hint
-
Note that \(\measuredangle AA'B = \pm \dfrac{\pi}{2}\) and \(\measuredangle AB'B = \pm \dfrac{\pi}{2}\). Then apply Corollary \(\PageIndex{2}\) to \(\square AA'BB'\).
If \(O\) is the center of the circle, then \(\measuredangle AOB \equiv 2 \cdot \measuredangle AA'B \equiv \pi\). That is, \(O\) is the midpoint of \([AB]\).
Assume a line \(\ell\), a circle with its center on \(\ell\) and a point \(P \not\in \ell\) are given. Make a ruler-only construction of the perpendicular to \(\ell\) from \(P\).
- Hint
-
Guess the construction from the diagram. To prove it, apply Theorem 8.2.1 and Corollary \(\PageIndex{1}\).
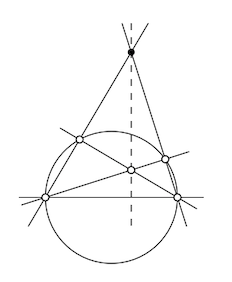
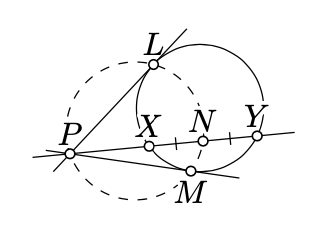
Suppose that lines \(\ell\), \(m\) and \(n\) pass thru a point \(P\); the lines \(\ell\) and \(m\) are tangent to a circle \(\Gamma\) at \(L\) and \(M\); the line \(n\) intersects \(\Gamma\) at two points \(X\) and \(Y\). Let \(N\) be the midpoint of \([XY]\). Show that the points \(P, L, M\), and \(N\) lie on one circle.
We say that a quadrangle \(ABCD\) is inscribed in circle \(\Gamma\) if all the points \(A, B, C\), and \(D\) lie on \(\Gamma\).
- Hint
-
Denote by \(O\) the center of \(\Gamma\). Use Corollary \(\PageIndex{1}\) to show that the point lie on the circle with diameter \([PO]\).
A nondegenerate quadrangle \(ABCD\) is inscribed in a circle if and only if
\(2 \cdot \measuredangle ABC \equiv 2 \cdot \measuredangle ADC.\)
- Proof
-
Since \(\square ABCD\) is nondegenerate, so is \(\triangle ABC\). Let \(O\) and \(\Gamma\) denote the circulcenter and circumcircle of \(\triangle ABC\) (they exist by Exercise 8.1.1).
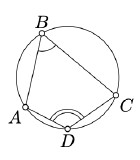
According to Theorem 9.2.1,
\(2 \cdot \measuredangle ABC \equiv \measuredangle AOC\).
From the same theorem, \(D \ni \Gamma\) if and only if
\(2 \cdot \measuredangle ADC \equiv \measuredangle AOC,\)
hence the result.
Let \(\Gamma\) and \(\Gamma'\) be two circles that intersect at two distinct point: \(A\) and \(B\). Assume \([XY]\) and \([X'Y']\) are the chords of \(\Gamma\) and \(\Gamma'\) respectively, such that \(A\) lies between \(X\) and \(X'\) and \(B\) lies between \(Y\) and \(Y'\). Show that \((XY) \parallel (X'Y')\).
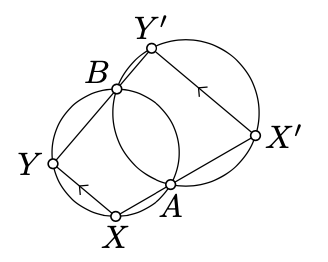
- Hint
-
Apply Corollary \(\PageIndex{2}\) twice for \(\square ABYX\) and \(\square ABY'X'\) and use the transversal property (Theorem 7.3.1).


