9.5: Arcs of circlines
- Page ID
- 23637
A subset of a circle bounded by two points is called a circle arc.
More precisely, suppose \(A, B, C\) are distinct points on a circle \(\Gamma\). The circle arc \(ABC\) is the subset that includes the points \(A, C\) as well as all the points on \(\Gamma\) that lie with \(B\) on the same side of \((AC)\).
For the circle arc \(ABC\), the points \(A\) and \(C\) are called endpoints. There are precisely two circle arcs of \(\Gamma\) with the given endpoints; they are opposite to each other.
Suppose \(X\) be another point on \(\Gamma\). By Corollary 9.3.2 we have that \(2 \cdot \measuredangle AXC \equiv 2 \cdot \measuredangle ABC\); that is,
\(\measuredangle AXC \equiv \measuredangle ABC\) or \(\measuredangle AXC \equiv \measuredangle ABC + \pi.\)
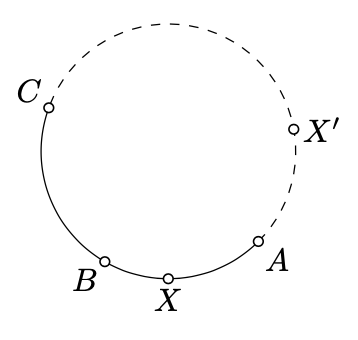
Recall that \(X\) and \(B\) lie on the same side from \((AC)\) if and only if \(\angle AXC\) and \(\angle ABC\) have the same sign (see Exercise 3.4.2). It follows that
- \(X\) lies on the arc \(ABC\) if and only if
\(\measuredangle AXC \equiv \measuredangle ABC\);
- \(X\) lies on the arc opposite to \(ABC\) if
\(\measuredangle AXC \equiv \measuredangle ABC + \pi\).
Note that a circle arc \(ABC\) is defined if \(\triangle ABC\) is not degenerate. If \(\triangle ABC\) is degenerate, then arc \(ABC\) is defined as a subset of line bounded by \(A\) and \(C\) that contain \(B\).
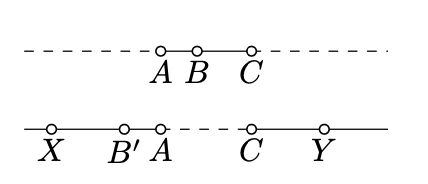
More precisely, if \(B\) lies between \(A\) and \(C\), then the arc \(ABC\) is defined as the line segment \([AC]\). If \(B'\) lies on the extension of \([AC]\), then the arc \(AB'C\) is defined as a union of disjoint half-lines \([AX)\) and \([CY)\) in \((AC)\). In this case the arcs \(ABC\) and \(AB'C\) are called opposite to each other.
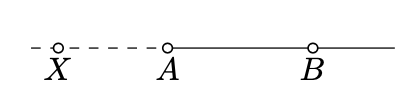
In addition, any half-line \([AB)\) will be regarded as an arc. If \(A\) lies between \(B\) and \(X\), then \([AX)\) will be called oppostie to \([AB)\). This degenerate arc has only one endpoint \(A\).
It will be convenient to use the notion of circline, that means circle or line. For example any arc is a subset of a circline; we also may use the term circline arc if we want to emphasise that the arc might be degenerate. Note that for any three distinct points \(A, B\), and \(C\) there is a unique circline arc \(ABC\).
The following statement summarizes the discussion above.
Let \(ABC\) be a circline arc and \(X\) be a point distinct from \(A\) and \(C\). Then
(a) \(X\) lies on the arc \(ABC\) if and only if
\(\measuredangle AXC = \measuredangle ABC;\)
(b) \(X\) lies on the arc opposite to \(ABC\) if and only if
\(\measuredangle AXC \equiv \measuredangle ABC + \pi\);
Given an acute triangle \(ABC\) make a compass-and-ruler construction of the point \(Z\) such that
\(\measuredangle AZB = \measuredangle BZC = \measuredangle CZA = \pm \dfrac{2}{3} \cdot \pi\)
- Hint
-
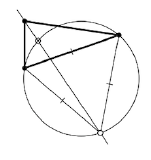
Guess a construction from the diagram. To show that it produces the needed point, apply Theorem 9.2.1.
Suppose that point \(P\) lies on the circumcircle of an equilateral triangle \(ABC\) and \(PA \le PB \le PC\). Show that \(PA + PB = PC\).
- Hint
-
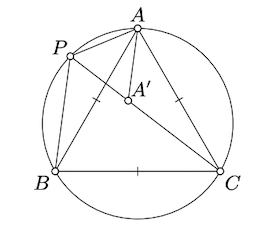
Show that \(P\) lies on the arc opposite from \(ACB\); conclude that \(\measuredangle APC = \measuredangle CPB = \pm \dfrac{\pi}{3}\).
Choose a point \(A' \in [PC]\) such that \(PA' = PA\). Note that \(\triangle APA'\) is equilateral. Prove and use that \(\triangle AA'C \cong \triangle APB.\)
A quadrangle \(ABCD\) is inscribed if all the points \(A, B, C\), and \(D\) lie on a circline \(\Gamma\). If the arcs \(ABC\) and \(ADC\) are opposite, then we say that the points \(A, B, C\), and \(D\) appear on \(\Gamma\) in the same cyclic order.
This definition makes it possible to formulate the following refinement of Corollary 9.3.2 which includes the degenerate quadrangles. It follows directly from Proposition \(\PageIndex{1}\).
A quadrangle \(ABCD\) is inscribed in a circline if and only if
\(\measuredangle ABC = \measuredangle ADC\) or \(\measuredangle ABC \equiv \measuredangle ADC + \pi.\)
Moreover, the second identity holds if and only if the points \(A,B,C,D\) appear on the circline in the same cyclic order.


