10.3: Inversive plane and circlines

Last updated
Save as PDF

Page ID: 23642

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Let $\Omega$ be a circle with the center $O$ and the radius r. Consider the inversion in $\Omega$.

Recall that the inverse of $O$ is undefined. To deal with this problem it is useful to add to the plane an extra point; it will be called the point at infinity; we will denote it as $\infty$. We can assume that ∞ is inverse of $O$ and the other way around.

The Euclidean plane with an added point at infinity is called the inversive plane.

We will always assume that any line and half-line contains $\infty$.

Recall that circline, means circle or line. Therefore we may say "if a circline contains $\infty$, then it is a line" or "a circline that does not contain $\infty$ is a circle".

Note that according to Theorem 8.1.1, for any $\triangle ABC$ there is a unique circline that passes thru $A, B$, and $C$ (if $\triangle ABC$ is degenerate, then this is a line and if not it is a circle).

Theorem $\PageIndex{1}$

In the inversive plane, inverse of a circline is a circline.

Proof

Suppose that $O$ denotes the center of the inversion and $r$ its radius.

Let $\Gamma$ be a circline. Choose three distinct points $A,B$, and $C$ on $\Gamma$. (If $\triangle ABC$ is nondegenerate, then $\Gamma$ is the circumcircle of $\triangle ABC$; if $\triangle ABC$ is degenerate, then $\Gamma$ is the line passing thru $A, B$, and $C$.)

Let $A', B'$, and $C'$ denote the inverses of $A, B$, and $C$ respectively. Let $\Gamma'$ be the circline that passes thru $A', B'$, and $C'$.

Assume $D$ is a point of the inversive plane that is distinct from $A, C, O$, and $\infty$. Suppose that $D'$ denotes the inverse of $D$.

By Theorem 10.2.6c, $D' \in \Gamma'$ if and only if $D \in \Gamma$.

It remains to prove that $O \in \Gamma \Leftrightarrow \infty \in \Gamma'$ and $\infty \in \Gamma \Leftrightarrow O \in \Gamma'$. Since $\Gamma$ is the inverse of $\Gamma'$, it is sufficient to prove that

$\infty \in \Gamma \Leftrightarrow O \in \Gamma'.$

If $\infty \in \Gamma$, then $\Gamma$ is a line; or, equivalently, for any $\varepsilon > 0$, the circline $\Gamma$ contains a point $P$ with $OP > r/\varepsilon$. For the inversion $P' \in \Gamma'$ of $P$, we have that $OP' = r^2/OP < r \cdot \varepsilon$. That is, the circline $\Gamma'$ contains points arbitrarily close to $O$. It follows that $O \in \Gamma'$. The same way we can check the converse.

Exercise $\PageIndex{1}$

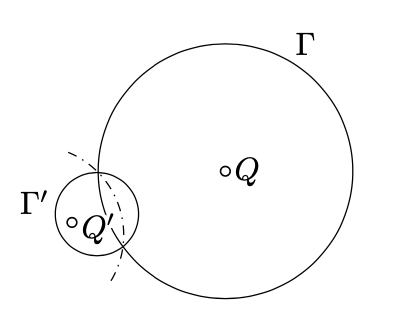
Assume that the circle $\Gamma'$ is the inverse of the circle $\Gamma$. Suppose that $Q$ denotes the center of $\Gamma$ and $Q'$ denotes the inverse of $Q$. Show that $Q'$ is not the center of $\Gamma'$.

$截屏2021-02-22 上午9.32.43.png$

Hint

First show that for any $r>0$ and for any real numbers $x,y$ distinct from 0,

$\dfrac{r^2}{(x + y)/2} = (\dfrac{r^2}{x} + \dfrac{r^2}{y})/2$

if and only if $x = y$.

Suppose that $\ell$ denotes the line passing thru $Q$, $Q'$, and the center of the inversion $O$. Choose an isometry $\ell \to \mathbb{R}$ that sends $O$ to 0; assume $x, y \in \mathbb{R}$ are the values of $\ell$ for the two points of intersection $\ell \cap \Gamma$; note that $x \ne y$. Assume $r$ is the radius of the circle of inversion. Then the left hand side above is the coordinate of $Q'$ and the right hand side is the coordinate of the center of $\Gamma'$.

Assume that a circumtool is a geometric construction tool that produces a circline passing thru any three given points.

Exercise $\PageIndex{2}$

Show that with only a circumtool, it is impossible to construct the center of a given circle.

Hint: A solution is given in Section 19.4.

Exercise $\PageIndex{3}$

Show that for any pair of tangent circles in the inversive plane, there is an inversion that sends them to a pair of parallel lines.

Hint: Apply an inversion in a circle with the center at the only point of intersection of the circles; then use Theorem $\PageIndex{2}$

Theorem $\PageIndex{2}$

Consider the inversion of the inversive plane in the circle $\Omega$ with the center $O$. Then

(a) A line passing thru $O$ is inverted into itself.

(b) A line not passing thru $O$ is inverted into a circle that passes thru $O$, and the other way around.

Proof

In the proof we use Theorem $\PageIndex{1}$ without mentioning it.

(a). Note that if a line passes thru $O$, it contains both $\infty$ and $O$. Therefore, its inverse also contains $\infty$ and $O$. In particular, the image is a line passing thru $O$.

(b). Since any line $\ell$ passes thru $\infty$, its image $\ell'$ has to contain $O$. If the line does not contain $O$, then $\ell' \not\ni \infty$; that is, $\ell'$ is not a line. Therefore, $\ell'$ is a circle that passes thru $O$.

(c). If the circle $\Gamma$ does not contain $O$, then its image $\Gamma'$ does not contain $\infty$. Therefore, $\Gamma'$ is a circle. Since $\Gamma \not\ni \infty$ we get that $\Gamma' \ni O$. Hence the result.

Theorem \(\PageIndex{1}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Theorem \(\PageIndex{2}\)