11.2: Two angles of a triangle
- Page ID
- 23648
In this section we will prove a weaker form of Theorem 7.4.1 which holds in any neutral plane.
Let \(\triangle ABC\) be a nondegenerate triangle in the neutral plane. Then
\(|\measuredangle CAB| + |\measuredangle ABC| < \pi.\)
Note that according to Theorem 3.3.1, the angles \(ABC, BCA\), and \(CAB\) have the same sign. Therefore, in the Euclidean plane the theorem follows immediately from Theorem 7.4.1.
- Proof
-
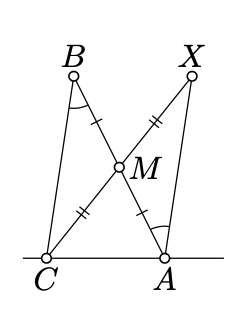
Let \(X\) be the reflection of \(C\) across the midpoint \(M\) of \([AB]\). By Proposition 7.2.1 \(\measuredangle BAX = \measuredangle ABC\) and therefore
\[\measuredangle CAX \equiv \measuredangle CAB + \measuredangle ABC.\]
Since \([BM]\) and \([MX]\) do not intersect \((CA)\), the points \(B\), \(M\), and \(X\) lie on the same side of \((CA)\). Therefore the angles \(CAB\) and \(CAX\) have the same sign. By Theorem 3.3.1, the angles \(CAB, ABC\) have the same sign; that is all angles in 11.2.1 have the same sign.
Note that \(\measuredangle CAX \not\equiv \pi\), otherwise \(X\) would lie on \((AC)\). Therefore the identity 11.2.1 implies that
\(|\measuredangle CAB|+|\measuredangle ABC|=|\measuredangle CAX| < \pi.\)
Assume \(A,B,C\), and \(D\) are points in a neutral plane such that
\(2 \cdot \measuredangle ABC + 2 \cdot \measuredangle BCD \equiv 0.\)
Show that \((AB)\parallel (CD)\).
Note that one cannot apply the transversal property (Theorem 7.3.1)
- Hint
-
Arguing by contradiction, assume \(2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 0\), but \((AB) \nparallel (CD)\). Let \(Z\) be the point of intersection of \((AB)\) and \((CD)\).
Note that \(2 \cdot \measuredangle ABC \equiv 2 \cdot \measuredangle ZBC\), and \(2 \cdot \measuredangle BCD \equiv 2 \cdot \measuredangle BCZ\).
Apply Proposition \(\PageIndex{1}\) to \(\triangle ZBC\) and try to arrive at a contradiction.
Prove the side-angle-angle congruence condition in the neutral geometry.
In other words, let \(ABC\) and \(A'B'C'\) be two triangles in a neutral plane; suppose that \(\triangle A'B'C'\) is nondegenerate. Show that \(\triangle ABC \cong \triangle A'B'C'\) if
\(AB = A'B'\), \(\measuredangle ABC = \pm \measuredangle A'B'C'\) and \(\measuredangle BCA = \pm \measuredangle B'C'A'.\)
- Hint
-
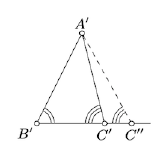
Let \(C'' \in [B'C')\) be the point such that \(B'C'' = BC\).
Note that by SAS, \(\triangle ABC \cong \triangle A'B'C''\). Conclude that \(\measuredangle B'C'A' = \measuredangle B'C''A'\).
Therefore, it is sufficient to show that \(C'' = C'\). If \(C' \ne C''\) apply Proposition \(\PageIndex{1}\) to \(\triangle A'C'C''\) and try to arrive at a contradiction.
Note that in the Euclidean plane, the above exercise follows from ASA and the theorem on the sum of angles of a triangle (Theorem 7.4.1). However, Theorem 7.4.1 cannot be used here, since its proof uses Axiom V. Later (Theorem 13.1.1) we will show that Theorem 7.4.1 does not hold in a neutral plane.
Assume that the point \(D\) lies between the vertices \(A\) and \(B\) of \(\triangle ABC\) in a neutral plane. Show that
\(CD < CA\) or \(CD < CB\).
- Hint
-
Use Exercise 5.2.2 and Proposition \(\PageIndex{1}\).
Alternatively, use the same argument as in the solution of Exercise 5.6.1.


