12.1: Conformal Disc Model
- Page ID
- 23654
In this section, we give new names for some objects in the Euclidean plane which will represent lines, angle measures, and distances in the hyperbolic plane. Let us fix a circle on the Euclidean plane and call it absolute. The set of points inside the absolute will be called the hyperbolic plane (or \(h\)-plane). Note that the points on the absolute do not belong to the h-plane. The points in the h-plane will be also called h-points.
Often we will assume that the absolute is a unit circle.
The intersections of the h-plane with circlines perpendicular to the absolute are called hyperbolic lines or h-lines.
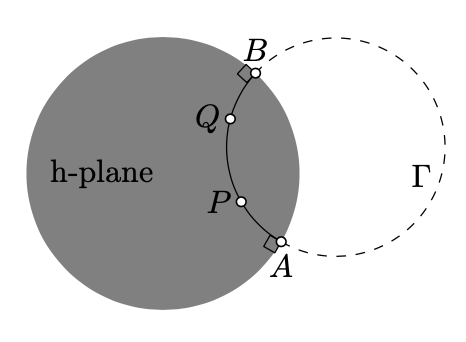
By Corollary 10.5.3, there is a unique h-line that passes thru the given two distinct h-points \(P\) and \(Q\). This h-line will be denoted by \((PQ)_h\).
The arcs of hyperbolic lines will be called hyperbolic segments or h-segments. An h-segment with endpoints \(P\) and \(Q\) will be denoted by \([PQ]_h\).
The subset of an h-line on one side from a point will be called a hyperbolic half-line (or h-half-line). More precisely, an h-half-line is an intersection of the h-plane with arc perpendicular to the absolute that has exactly one of its endpoints in the h-plane. An h-half-line starting at \(P\) and passing thru \(Q\) will be denoted by \([PQ)_h\).
If \(\Gamma\) is the circline containing the h-line \((PQ)_h\), then the points of intersection of \(\Gamma\) with the absolute are called ideal points of \((PQ)_h\). (Note that the ideal points of an h-line do not belong to the h-line.)
An ordered triple of h-points, say \((P,Q,R)\) will be called h-triangle \(PQR\) and denoted by \(\triangle_h P Q R\).
Let us point out, that so far an h-line \((PQ)_h\) is just a subset of the h-plane; below we will introduce h-distance and later we will show that \((PQ)_h\) is a line for the h-distance in the sense of the Definition 1.5.1.
Show that an h-line is uniquely determined by its ideal points.
- Hint
-
Let \(A\) and \(B\) be the ideal points of the h-line \(\ell\). Note that the center of the Euclidean circle containing \(\ell\) lies at the intersection of the lines tangent to the absolute at the ideal points of \(\ell\).
Show that an h-line is uniquely determined by one of its ideal points and one h-point on it.
- Hint
-
Assume \(A\) is an ideal point of the h-line \(\ell\) and \(P \in \ell\). Suppose that \(P'\) denotes the inverse of \(P\) in the absolute. By Corollary 10.5.1, \(\ell\) lies in the intersection of the h-plane and the (necessarily unique) circline passing thru \(P, A\), and \(P'\)
Show that the h-segment \([PQ]_h\) coincides with the Euclidean segment \([PQ]\) if and only if the line \((PQ)\) pass thru the center of the absolute.
- Hint
-
Let \(\Omega\) and \(O\) denote the absolute and its center.
Let \(\Gamma\) be the circline containing \([PQ]_h\). Note that \([PQ]_h = [PQ]\) if and only if \(\Gamma\) is a line.
Suppose that \(P'\) denotes the inverse of \(P\) in \(\Omega\). Note that \(O, P\), and \(P'\) lie on one line.
By the definition of h-line, \(\Omega \perp \Gamma\). By Corollary 10.5.1, \(\Gamma\) passes thru \(P\) and \(P'\). Therefore, \(\Gamma\) is a line if and only if it pass thru \(O\).
Let \(P\) and \(Q\) be distinct h-points; let \(A\) and \(B\) denote the ideal points of \((PQ)_h\). Without loss of generality, we may assume that on the Euclidean circline containing the h-line \((PQ)_h\), the points \(A,P,Q,B\) appear in the same order.
Consider the function
\(\delta(P,Q):= \dfrac{AQ \cdot PB}{AP \cdot QB}.\)
Note that the right hand side is a cross-ratio; by Theorem 10.2.1 it is invariant under inversion. Set \(\delta(P,P)=1\) for any h-point \(P\). Let us define h-distance as the logarithm of \(\delta\); that is,
\(PQ_h := \ln[\delta(P,Q)].\)
The proof that \(PQ_h\) is a metric on the h-plane will be given later. For now it is just a function that returns a real value \(PQ_h\) for any pair of h-points \(P\) and \(Q\).
Let \(O\) be the center of the absolute and the h-points \(O\), \(X\), and \(Y\) lie on one h-line in the same order. Assume \(OX=XY\). Prove that \(OX_h<XY_h\).
- Hint
-
Assume that the absolute is a unit circle.
Set \(a = OX = OY\). Note that \(0 < a < \dfrac{1}{2}\), \(OX_h = \ln \dfrac{1+ a}{1 -a}\), and \(XY_h = \ln \dfrac{(1 + 2 \cdot a) \cdot (1 - a)}{(1 - 2 \cdot a)\cdot (1 + a)}\). It remains to check that the inequalities
\(1 < \dfrac{1 + a}{1 - a} < \dfrac{(1 + 2 \cdot a) \cdot (1 - a)}{(1 - 2 \cdot a)\cdot (1 + a)}\)
hold if \(0 < a < \dfrac{1}{2}\).
Consider three h-points \(P\), \(Q\), and \(R\) such that \(P\ne Q\) and \(R\ne Q\). The hyperbolic angle \(PQR\) (briefly \(\angle_h PQR\)) is an ordered pair of h-half-lines \([QP)_h\) and \([QR)_h\).
Let \([QX)\) and \([QY)\) be (Euclidean) half-lines that are tangent to \([QP]_h\) and \([QR]_h\) at \(Q\). Then the hyperbolic angle measure (or h-angle measure) of \(\angle_h PQR\) denoted by \(\measuredangle_h PQR\) and defined as \(\measuredangle XQY\).
Let \(\ell\) be an h-line and \(P\) be an h-point that does not lie on \(\ell\). Show that there is a unique h-line passing thru \(P\) and perpendicular to \(\ell\).
- Hint
-
Spell the meaning of terms "perpendicular" and "h-line" and then apply Exercise 10.5.4.


