13.1: Angle of parallelism

Last updated
Save as PDF

Page ID: 23661

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Let $P$ be a point off an h-line $\ell$. Drop a perpendicular $(PQ)_h$ from $P$ to $\ell$; let $Q$ be its foot point. Let $\phi$ be the smallest value such that the h-line $(PZ)_h$ with $|\measuredangle_h Q P Z|=\phi$ does not intersect $\ell$.

The value $\phi$ is called the angle of parallelism of $P$ to $\ell$. Clearly, $\phi$ depends only on the h-distance $s=PQ_h$. Further, $\phi(s) \to \pi/2$ as $s \to 0$, and $\phi(s) \to 0$ as $s \to \infty$. (In the Euclidean geometry, the angle of parallelism is identically equal to $\pi/2$.)

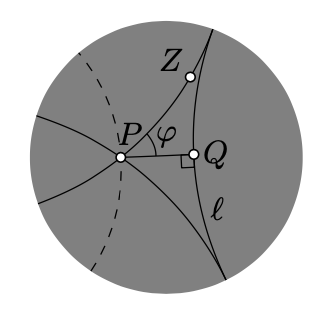
$截屏2021-02-24 下午2.07.43.png$

If $\ell$, $P$, and $Z$ are as above, then the h-line $m=(PZ)_h$ is called asymptotically parallel to $\ell$. In other words, two h-lines are asymptotically parallel if they share one ideal point. (In hyperbolic geometry, the term parallel lines is often used for asymptotically parallel lines; we do not follow this convention.)

Given $P \not\in \ell$, there are exactly two asymptotically parallel lines thru $P$ to $\ell$; the remaining parallel lines are called ultra parallel.

On the diagram, the two solid h-lines passing thru $P$ are asymptotically parallel to $\ell$; the dashed h-line is ultra parallel to $\ell$.

Exercise $\PageIndex{1}$

Show that two distinct h-lines $\ell$ and $m$ are ultraparallel if and only if they have a common perpendicular; that is, there is an $h$-line $n$ such that $n \perp \ell$ and $n \perp m$.

Hint

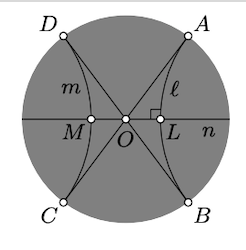
$截屏2021-02-24 下午2.24.54.png$

"only-if" part. Suppose $\ell$ and $m$ are ultraparallel; that is, they do not intersect and have distinct ideal points. Denote the ideal points by $A, B, C$, and $D$; we may assume that they appear on the absolute in the same order. In this case the h-line with ideal points $A$ and $C$ intersects the h-line with ideal points $B$ and $D$. Denote by $O$ their point of intersection.

By Lemma 12.3.1, we can assume that $O$ is the center of absolute. Note that $\ell$ is the reflection of $m$ across $O$ in the Euclidean sense. Drop an h-perpendicular $n$ from $O$ to $\ell$, and show that $n \perp m$.

"If" part. Suppose $n$ is a common perpendicular. Denote by $L$ and $M$ its points of intersection with $\ell$ and $m$ respectively. By Lemma 12.3.1, we can assume that the center of absolute $O$ is the h-midpoint of $L$ and $M$. Note that in this case $\ell$ is the reflection of m across $O$ in the Euclidean sense. It follows that the ideal points of the h-lines $\ell$ and $m$ are symmetric to each other. Therefore, if one pair of them coincides, then so is the other pair. By Exercise 12.1.1, $\ell = m$, which contradicts the assumption $\ell \ne m$.

Proposition $\PageIndex{1}$

Let $Q$ be the foot point of $P$ on h-line $\ell$. Then

$PQ_h=\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi},$

where $\phi$ is the angle of parallelism of $P$ to $\ell$.

In particular, if $P \notin \ell$ and $\beta =|\measuredangle_h XPY|$ for some points $X,Y\in\ell$, then

$PQ_h < \dfrac{1}{2} \cdot \ln \dfrac{1+\cos \dfrac{\beta}{2}}{1- \cos \dfrac{\beta}{2}}.$

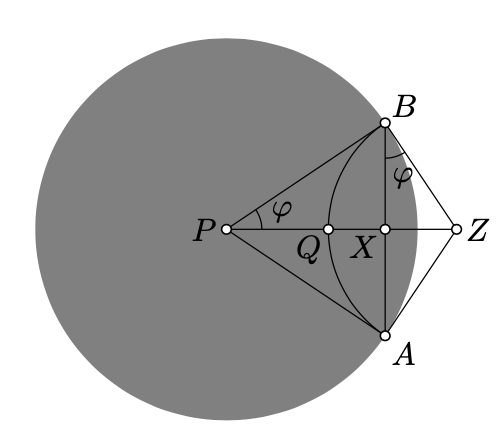
$截屏2021-02-24 下午2.16.20.png$

Proof

Applying a motion of the h-plane if necessary, we may assume $P$ is the center of the absolute. Then the h-lines thru $P$ are the intersections of Euclidean lines with the h-plane.

Let $A$ and $B$ denote the ideal points of $\ell$. Without loss of generality, we may assume that $\angle APB$ is positive. In this case

$\phi=\measuredangle QPB=\measuredangle APQ=\dfrac{1}{2} \cdot\measuredangle APB.$

Let $Z$ be the center of the circle $\Gamma$ containing the h-line $\ell$. Set $X$ to be the point of intersection of the Euclidean segment $[AB]$ and the line $(PQ)$.

Note that, $PX = \cos \phi$. Therefore, by Lemma 12.3.2,

$PX_h=\ln \dfrac{1+\cos\phi}{1-\cos\phi}.$

Note that both angles $PBZ$ and $BXZ$ are right. Since the angle $PZB$ is shared, $\triangle ZBX \sim \triangle ZPB$. In particular,

$ZX \cdot ZP = ZB^2;\]$

that is, $X$ is the inverse of $P$ in $\Gamma$.

The inversion in $\Gamma$ is the reflection of the h-plane across $\ell$. Therefore

$\begin{array} {rcl} {PQ_h} & = & {QX_h =} \\ {} & = & {\dfrac{1}{2} \cdot PX_h =} \\ {} & = & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \phi}{1 - \cos \phi}.} \end{array}$

The last statement follows since $\phi > \dfrac{\beta}{2}$ and the function

is decreasing in the interval $(0,\dfrac{\pi}{2}]$.

Exercise $\PageIndex{2}$

Let $ABC$ be an equilateral h-triangle with side $100$. Show that

$|\measuredangle_h ABC|<\frac1{10\ 000\ 000\ 000}.$

Hint: By triangle inequality, the h-distance from $B$ to $(AC)_h$ is at least 50. It remains to estimate $|\measuredangle_h ABC| using Proposition \(\PageIndex{1}$. The inequalities $\cos \phi \le 1 - \dfrac{1}{10} \cdot \phi^2$ for $|\phi| < \dfrac{\pi}{2}$ and $e^3 > 10$ should help to finish the proof.

Exercise \(\PageIndex{1}\)

Proposition \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)