13.4: Hyperbolic triangles
- Page ID
- 23664
Any nondegenerate hyperbolic triangle has a positive defect.
- Proof
-
Fix an h-triangle \(ABC\). According to Theorem 11.3.1,
\[\text{defect}(\triangle_hABC)\ge 0\]
It remains to show that in the case of equality, \(\triangle_hABC\) degenerates.
Without loss of generality, we may assume that \(A\) is the center of the absolute; in this case \(\measuredangle_h CAB = \measuredangle CAB\). Yet we may assume that
\(\measuredangle_h CAB\), \(\measuredangle_h ABC\), \(\measuredangle_h BCA\), \( \measuredangle ABC\), \(\measuredangle BCA \ge 0.\)
Let \(D\) be an arbitrary point in \([CB]_h\) distinct from \(B\) and \(C\). From Proposition 9.6.1, we have
\(\measuredangle ABC-\measuredangle_h ABC \equiv \pi-\measuredangle CDB \equiv \measuredangle BCA-\measuredangle_h BCA.\)
From Exercise 7.4.2, we get that
Therefore, if we have equality in 13.4.1, then \(\measuredangle CDB=\pi\). In particular, the h-segment \([BC]_h\) coincides with the Euclidean segment \([BC]\). By Exercise 12.1.3, the latter can happen only if the h-line \((BC)_h\) passes thru the center of the absolute (\(A\)); that is, if \(\triangle_hABC\) degenerates.
The following theorem states, in particular, that nondegenerate hyperbolic triangles are congruent if their corresponding angles are equal. In particular, in hyperbolic geometry, similar triangles have to be congruent.
Two nondegenerate h-triangles \(ABC\) and \(A'B'C'\) are congruent if \(\measuredangle_hABC = \pm \measuredangle_hA'B'C'\), \(\measuredangle_hBCA = \pm \measuredangle_h B'C'A'\) and \(\measuredangle_hCAB = \pm \measuredangle_hC'A'B'\).
- Proof
-
Note that if \(AB_h=A'B'_h\), then the theorem follows from ASA.
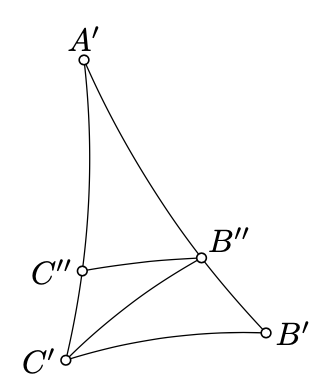
Assume the contrary. Without loss of generality, we may assume that \(AB_h<A'B'_h\). Therefore, we can choose the point \(B''\in [A'B']_h\) such that \(A'B''_h=AB_h\).
Choose an h-half-line \([B''X)\) so that
\(\measuredangle_h A'B''X=\measuredangle_h A'B'C'.\)
According to Exercise 11.5, \((B''X)_h\parallel(B'C')_h\).
By Pasch’s theorem (Theorem 3.12), \((B''X)_h\) intersects \([A'C']_h\). Suppose that \(C''\) denotes the point of intersection.
According to ASA, \(\triangle_h ABC\cong\triangle_h A'B''C''\); in particular,
\[\text{defect}(\triangle_h ABC)=\text{defect}(\triangle_h A'B''C'').\]
Applying Exercise 11.11 twice, we get that
\[\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {\text{defect} (\triangle_h A'B''C'') +} \\ {} & + & {\text{defect}(\triangle_h B''C''C') + \text{defect} (\triangle_h B''C'B').} \end{array}\]
By Theorem 13.7, all the defects have to be positive. Therefore
\(\text{defect} (\triangle_h A'B'C') > \text{defect} (\triangle_h ABC).\)
On the other hand,
\(\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {|\measuredangle_h A'B'C'| + |\measuredangle_h B'C'A'| + |\measuredangle_h C'A'B'| =} \\ {} & = & {|\measuredangle_h ABC| + |\measuredangle_BCA| + |\measuredangle_h CAB|} \\ {} & = & {\text{defect} (\triangle_h ABC)} \end{array}\)
— a contradiction.
Recall that a bijection from a h-plane to itself is called angle preserving if
\(\measuredangle_h ABC= \measuredangle_h A'B'C'\)
for any \(\triangle_h ABC\) and its image \(\triangle_h A'B'C'\).
Show that any angle-preserving transformation of the h-plane is a motion.
- Hint
-
Apply AAA-congruence condition (Theorem \(\PageIndex{2}\))


