13.6: Pythagorean theorem
- Page ID
- 23666
Recall that \(\cosh\) denotes hyperbolic cosine; that is, the function defined by
\(\cosh x := \dfrac{e^x+e^{-x}}2.\)
Assume that \(ACB\) is an h-triangle with right angle at \(C\). Set
\(a = BC_h,\) \(b = CA_h\) and \(c = AB_h\).
Then
\[\cosh c = \cosh a \cdot \cosh b.\]
The formula 13.6.1 will be proved by means of direct calculations. Before giving the proof, let us discuss the limit cases of this formula.
Note that \(\cosh x\) can be written using the Taylor expansion
\(\cosh x=1+\dfrac{1}{2}\cdot x^2+\dfrac{1}{24}\cdot x^4+\dots.\)
It follows that if \(a\), \(b\), and \(c\) are small, then
\(\begin{array} {rcl} {1 + \dfrac{1}{2} \cdot c^2} & \approx & {\cosh c = \cosh a \cdot \cosh b \approx} \\ {} & \approx & {(1 + \dfrac{1}{2} \cdot a^2)(1 + \dfrac{1}{2} \cdot b^2) \approx} \\ {} & \approx & {1 + \dfrac{1}{2} \cdot (a^2 + b^2).} \end{array}\)
In other words, the original Pythagorean theorem (Theorem 6.2.1) is a limit case of the hyperbolic Pythagorean theorem for small triangles.
For large \(a\) and \(b\) the terms \(e^{-a}\), \(e^{-b}\), and \(e^{-a-b+\ln 2}\) are neglectable. In this case we have the following approximations:
\(\begin{array} {\cosh a \cdot \cos h b} & \approx & {\dfrac{e^a}{2} \cdot \dfrac{e^b}{2} =} \\ {} & = & {\dfrac{e^{a+b-\ln 2}}{2} \approx} \\ {} & \approx & {\cosh (a+b-\ln 2)} \end{array}\)
Therefore \(c \approx a+b-\ln 2\).
Assume that \(ACB\) is an h-triangle with right angle at \(C\). Set \(a=BC_h\), \(b=CA_h\), and \(c=AB_h\). Show that
\(c+\ln 2>a+b.\)
- Hint
-
Apply the hyperbolic Pythagorean theorem and the definition of hyperbolic cosine. The following observations should help:
- \(x \mapsto e^x\) is an increasing positive function.
- By the triangle inequality, we have \(-c \le a - b\) and \(-c \le b - a\)
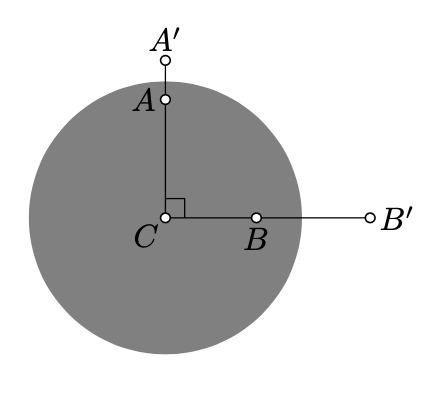
In the proof of the hyperbolic Pythagorean theorem we use the following formula from Exercise 12.9.2:
here \(A\), \(B\) are h-points distinct from the center of absolute and \(A'\), \(B'\) are their inversions in the absolute. This formula is derived in the hints.
Proof of Theorem \(\PageIndex{1}\). We assume that absolute is a unit circle. By the main observation (Theorem 12.3.1) we can assume that \(C\) is the center of absolute. Let \(A'\) and \(B'\) denote the inverses of \(A\) and \(B\) in the absolute.
Set \(x=BC\), \(y=AC\). By Lemma Theorem 12.3.2
\(a = \ln \dfrac{1 + x}{1 - x}\), \(b = \ln \dfrac{1 + y}{1 - y}.\)
Therefore
\[\begin{array} {rclcrcl} {\cosh a} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + x}{1 - x} + \dfrac{1 - x}{1 + x}) =} & \ \ \ \ & {\cosh b} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + y}{1 - y} + \dfrac{1 - y}{1 + y}) =} \\ {} & = & {\dfrac{1 + x^2}{1-x^2},} & \ \ \ \ & {} & = & {\dfrac{1 + y^2}{1 - y^2}.} \end{array}\]
Note that
\(B'C = \dfrac{1}{x},\) \(A'C = \dfrac{1}{y}.\)
Therefore
\(BB' = \dfrac{1}{x} - x\), \(AA' = \dfrac{1}{y} - y.\)
Since the triangles \(ABC\), \(A'BC\), \(AB'C\), \(A'B'C\) are right, the original Pythagoran theorem (Theorem 6.2.1) implies
\(\begin{array} {rcl} {AB} & = & {\sqrt{x^2 + y^2}} \\ {A'B} & = & {\sqrt{x^2 + \dfrac{1}{y^2}},} \end{array}\) \(\begin{array} {rcl} {AB'} & = & {\sqrt{\dfrac{1}{x^2} + y^2,}} \\ {A'B'} & = & {\sqrt{\dfrac{1}{x^2} + \dfrac{1}{y^2}}.} \end{array}\)
According to Exercise 12.9.2,
\[\begin{array} {rcl} {\cosh c} & = & {\dfrac{AB \cdot A'B' + AB' \cdot A'B}{AA' \cdot BB'} = } \\ {} & = & {\dfrac{\sqrt{x^2 + y^2} \cdot \sqrt{\dfrac{1}{x^2} + \dfrac{1}{y^2}} + \sqrt{\dfrac{1}{x^2} + y^2} \cdot \sqrt{x^2 + \dfrac{1}{y^2}}}{(\dfrac{1}{y} - y) \cdot (\dfrac{1}{x} - x)} =} \\ {} & = & {\dfrac{x^2 + y^2 + 1 + x^2 \cdot y^2}{(1 - y^2) \cdot (1 - x^2)} =} \\ {} & = & {\dfrac{1 + x^2}{1 - x^2} \cdot \dfrac{1 + y^2}{1 - y^2}.} \end{array}\]
Finally note that 13.6.2 and 13.6.3 imply 13.6.1.


