14.3: Fundamental Theorem of Affine Geometry
- Page ID
- 23670
Further we assume knowledge of vector algebra, namely multiplication by a real number, addition and the parallelogram rule.
Show that affine transformations map parallelograms to parallelograms. Conclude that if \(P\mapsto P'\) is an affine transformation, then
\(\overrightarrow{XY}=\overrightarrow{AB}\), \(\text{if and only if}\) \(\overrightarrow{X'Y'} =\overrightarrow{A'B'}.\)
- Hint
-
Apply twice Exercise 14.1.1 and the parallelogram rule. (Note that the case if \(A, B, X\), and \(Y\) are collinear requires extra work.)
Let \(P \mapsto P'\) be an affine transformation of the Euclidean plane. Then, for any triple of points \(O\), \(X\), \(P\), we have
\[\overrightarrow{OP}=t \cdot \overrightarrow{OX} \ \ \ \ \text{if and only if}\ \ \ \ \overrightarrow{O'P'} =t \cdot \overrightarrow{O'X'}.\]
- Proof
-
Observe that the affine transformations described in Exercise 14.1.2 as well as all motions satisfy the condition 14.3.1. Therefore a given affine transformation \(P \mapsto P'\) satisfies 14.3.1 if and only if its composition with motions and scalings satisfies 14.3.1.
Applying this observation, we can reduce the problem to its partial case. Namely, we may assume that \(O'=O\), \(X'=X\), the point \(O\) is the origin of a coordinate system, and \(X\) has coordinates \((1,0)\).
In this case, \(\overrightarrow{OP}=t\cdot \overrightarrow{OX}\) if and only if \(P=(t,0)\). Since \(O\) and \(X\) are fixed, the transformation maps the \(x\)-axis to itself. That is, \(P'=(f(t),0)\) for some function \(t\mapsto f(t)\), or, equivalently, \(\overrightarrow{O'P'}=f(t)\cdot \overrightarrow{O'X'}\). It remains to show that
\[f(t)=t \]
for any \(t\).
Since \(O'=O\) and \(X'=X\), we get that \(f(0)=0\) and \(f(1)=1\). Further, according to Exercise 14.2.2, we have that \(f(x\cdot y)=f(x)\cdot f(y)\) and \(f(x+y)=f(x)+f(y)\) for any \(x,y \in \mathbb{R}\). By the algebraic lemma (proved below, see Lemma 14.4.1), these conditions imply 14.3.2.
Suppose an affine transformation maps a nondegenerate triangle \(OXY\) to a triangle \(O'X'Y'\). Then \(\triangle O'X'Y'\) is nondegenerate, and
\(\overrightarrow{OP}=x \cdot \overrightarrow{OX} + y \cdot \overrightarrow{OY} \ \ \ \text{if and only if}\ \ \ \ \overrightarrow{O'P'} =x\cdot\overrightarrow{O'X'}+y\cdot\overrightarrow{O'Y'}.\)
- Proof
-
Since an affine transformation maps lines to lines, the triangle \(O'X'Y'\) is nondegenerate.
If \(x=0\) or \(y=0\), then the second statement follows directly from the proposition. Otherwise consider points \(V\) and \(W\) defined by
\(\overrightarrow{OV} = x \cdot \overrightarrow{OX}, \ \ \ \overrightarrow{OW} = y \cdot \overrightarrow{OY}.\)
By the proposition,
\(\overrightarrow{O'V'}=x\cdot\overrightarrow{O'X'}, \ \ \ \overrightarrow{O'W'} =y \cdot \overrightarrow{O'Y'}.\)
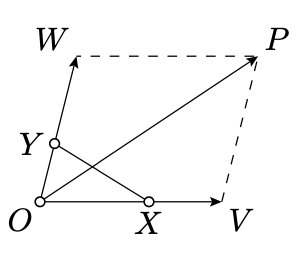
Note that
\(\overrightarrow{OP}=\overrightarrow{OV}+\overrightarrow{OW},\)
or, equivalently, \(\square OVPW\) is a parallelogram. According to Exercise 14.1.1, \(\square O'V'P'W'\) is a parallelogram as well. Therefore
\(\begin{array} {rcl} {\overrightarrow{O'P'}} & = & {\overrightarrow{O'V'} + \overrightarrow{O'W'} =} \\ {} & = & {x \cdot \overrightarrow{O'X'} + y \cdot \overrightarrow{O'Y'}} \end{array}\)
Show that any affine transformation is continuous.
- Hint
-
Fix a coordinate system and apply the fundamental theorem of affine geometry (Theorem \(\PageIndex{1}\)) for the points \(O = (0, 0), X = (1, 0)\) and \(Y = (0, 1)\).
The following exercise provides the converse to Exercise Exercise 14.1.2(d).
Show that any affine transformation can be written in coordinates as
\((x,y)\mapsto(a\cdot x+b\cdot y+r,c\cdot x+d\cdot y+s)\)
for constants \(a,b,c,d,r,s\) such that the matrix \((\begin{smallmatrix}a&b\\c&d\end{smallmatrix})\) is invertible.
- Hint
-
Fix a coordinate system and apply the fundamental theorem of affine geometry (Theorem \(\PageIndex{1}\)) for the points \(O = (0, 0), X = (1, 0)\) and \(Y = (0, 1)\).


