15.4: Perspective projection
- Page ID
- 23678
Consider two planes \(\Pi\) and \(\Pi'\) in the Euclidean space. Let \(O\) be a point that does not belong neither to \(\Pi\) nor \(\Pi'\).
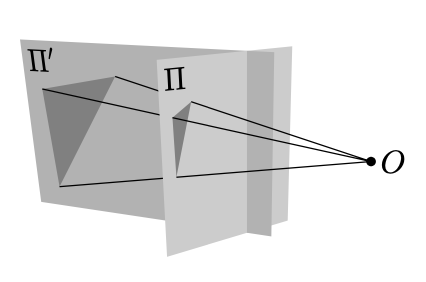
A perspective projection from \(\Pi\) to \(\Pi'\) with center at \(O\) maps a point \(P\in \Pi\) to the intersection point \(P'=\Pi'\cap (OP)\).
In general, perspective projection is not a bijection between the planes. Indeed, if the line \((OP)\) is parallel to \(\Pi'\) (that is, if \((OP)\cap\Pi'=\emptyset\)) then the perspective projection of \(P\in \Pi\) is undefined. Also, if \((OP')\parallel \Pi\) for \(P'\in \Pi'\), then the point \(P'\) is not an image of the perspective projection.
For example, let \(O\) be the origin of \((x,y,z)\)-coordinate space and the planes \(\Pi\) and \(\Pi'\) are given by the equations \(z=1\) and \(x=1\) respectively. Then the perspective projection from \(\Pi\) to \(\Pi'\) can be written in the coordinates as
\((x,y,1)\mapsto (1,\dfrac{y}{x},\dfrac{1}{x}).\)
Indeed the coordinates have to be proportional; points on \(\Pi\) have unit \(z\)-coordinate, and points on \(\Pi'\) have unit \(z\)-coordinate.
The perspective projection, maps one plane to another. However, we can identify the two planes by fixing a coordinate system in each. In this case we get a partially defined map from the plane to itself. We will keep the name perspective transformation for such maps.
For the described perspective projection; we may get the map
\[\beta\:(x,y)\mapsto (\dfrac{1}{x},\dfrac{y}{x}).\]
This map is undefined on the line \(x=0\). Also points on this line are not images of points under perspective projection.
Denote by \(\hat \Pi\) and \(\hat \Pi'\) the projective completions of \(\Pi\) and \(\Pi'\) respectively. Note that the perspective projection is a restriction of composition of the two bijections \(\hat \Pi\leftrightarrow\Phi \leftrightarrow\hat \Pi'\) constructed in the previous section. By Observation 15.3.1, the perspective projection can be extended to a bijection \(\hat \Pi\leftrightarrow\hat \Pi'\) that sends lines to lines. (A similar story happened with inversion. An inversion is not defined at its center; moreover, the center is not an inverse of any point. To deal with this problem we passed to the inversive plane which is the Euclidean plane extended by one ideal point. The same strategy worked for perspective projection \(\Pi \to \Pi'\), but this time we need to add an ideal line.)
For example, to define extension of the perspective projection \(\beta\) in 15.4.1, we have to observe that
- The pencil of vertical lines \(x=a\) is mapped to itself.
- The ideal points defined by pencil of lines \(y=m \cdot x+ b\) are mapped to the point \((0,m)\) and the other way around — point \((0, m)\) is mapped to the ideal point defined by the pencil of lines \(y=m \cdot x+ b\).


