15.8: Construction of a polar
- Page ID
- 58358
In this section we describe a powerful trick that can be used in the constructions with ruler.
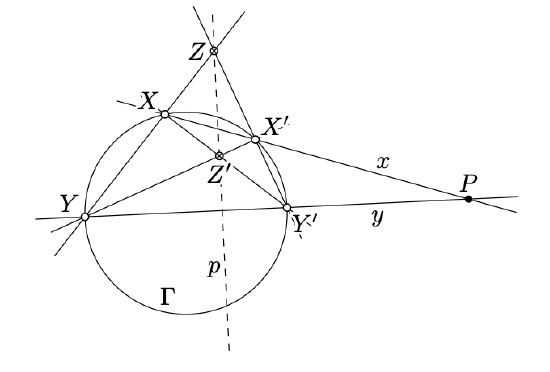
Assume \(\Gamma\) is a circle in the plane and \(P\notin \Gamma\).Draw two lines \(x\) and \(y\) thru \(P\) that intersect \(\Gamma\) at two pairs of points \(X\), \(X'\) and \(Y\), \(Y'\). Let \(Z=(XY) \cap (X'Y')\) and \(Z'=(XY') \cap(X'Y)\). Consider the line \(p=(ZZ')\).
The constructed line \(p=(ZZ')\) does not depend on the choice of the lines \(x\) and \(y\).
Moreover, \(P \leftrightarrow p\) can be extended to a duality such that any point \(P\) on the circle \(\Gamma\) corresponds to a line \(p\) tangent to \(\Gamma\) at \(P\).
We will use this claim without a proof, but the proof is not hard. If \(P\) lies outside of \(\Gamma\), it can be done by moving \(P\) to infinity keeping \(\Gamma\) fixed as a set. If \(P\) lies inside of \(\Gamma\), it can be done by moving \(P\) to the center of \(\Gamma\). The existence of corresponding projective transformations follow from the idea in Exercise 16.3.1.
The line \(p\) is called the polar of the point \(P\) with respect to \(\Gamma\).
The point \(P\) is called the pole of the line \(p\) with respect to \(\Gamma\).
Revert the described construction. That is, given a circle \(\Gamma\) and a line \(p\) that is not tangent to \(\Gamma\), construct a point \(P\) such that the described construction for \(P\) and \(\Gamma\) produces the line \(p\).
- Hint
-
Suppose \(p = (QR)\); denote by \(q\) and \(r\) the dual lines produced by the construction. Then, by Claim \(\PageIndex{1}\), \(P\) is the point of intersection of \(q\) and \(r\).
Let \(p\) be the polar line of point \(P\) with respect to the circle \(\Gamma\). Assume that \(p\) intersects \(\Gamma\) at points \(V\) and \(W\). Show that the lines \((PV)\) and \((PW)\) are tangent to \(\Gamma\).
Come up with a ruler-only construction of the tangent lines to the given circle \(\Gamma\) thru the given point \(P\not\in \Gamma\).
- Hint
-
The line \(v\) polar to \(V\) is tangent to \(\Gamma\). Since \(V \in p\), by Claim \(\PageIndex{1}\), we get that \(P \in v\); that is, \((PV) = v\). Hence the statement follows.
Assume two concentric circles \(\Gamma\) and \(\Gamma'\) are given. Construct the common center of \(\Gamma\) and \(\Gamma'\) with a ruler only.
- Hint
-
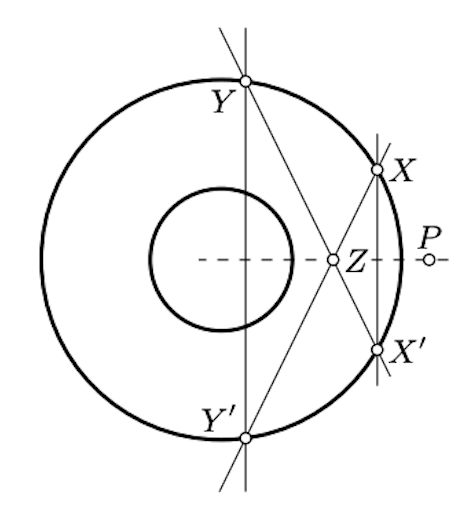
Choose a point \(P\) outside of the bigger circle. Construct the lines dual to \(P\) for both circles. Note that these two lines are parallel.
Assume that the lines intersect the bigger circle at two pairs of points \(X, X'\) and \(Y, Y'\). Set \(Z = (XY) \cap (X'Y')\). Note that the line \((PZ)\) passes thru the common center.
The center is the intersection of \((PZ)\) and another line constructed the same way.
Assume a line \(\ell\) and a circle \(\Gamma\) with its center \(O\) are given. Suppose \(O\notin \ell\). Construct a perpendicular from \(O\) on \(\ell\) with a ruler only.
- Hint
-
Construct polar liens to two point on \(\ell\). Denote by \(L\) the intersection of these two liens. Note that \(\ell\) is polar to \(L\) and therefore \((OL) \perp \ell\).

