16.2: Pythagorean Theorem

Last updated
Save as PDF

Page ID: 23683

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Here is an analog of the Pythagorean theorems (Theorem 6.2.1 and Theorem 13..1) in spherical geometry.

Theorem $\PageIndex{1}$ Spherical Pythagorean Theorem

Let $\triangle_sABC$ be a spherical triangle with a right angle at $C$. Set $a=BC_s$, $b=CA_s$, and $c=AB_s$. Then

$\cos c=\cos a \cdot \cos b.$

Proof

Since the angle at $C$ is right, we can choose the coordinates in $\mathbb{R}^3$ so that $v_C\z=(0,0,1)$, $v_A$ lies in the $xz$-plane, so $v_A=(x_A,0,z_A)$, and $v_B$ lies in $yz$-plane, so $v_B=(0,y_B,z_B)$.

Applying, 16.2.3, we get that

$\begin{aligned} z_A&=\langle v_C,v_A\rangle =\cos b, \\ z_B&=\langle v_C,v_B\rangle =\cos a.\end{aligned}$

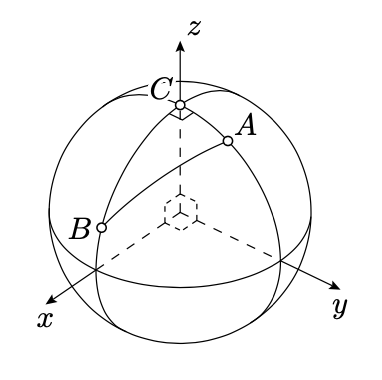
$截屏2021-02-26 上午11.19.37.png$

Applying, 16.2.1 and 16.2.3, we get that

$\begin{aligned} \cos c &=\langle v_A,v_B\rangle= \\ &=x_A\cdot 0+0\cdot y_B+z_A\cdot z_B= \\ &=\cos b\cdot\cos a.\end{aligned}$

In the proof, we will use the notion of the scalar product which we are about to discuss.

Let $v_A=(x_A,y_A,z_A)$ and $v_B=(x_B,y_B,z_B)$ denote the position vectors of points $A$ and $B$. The scalar product of the two vectors $v_A$ and $v_B$ in $\mathbb{R}^3$ is defined as

\[\langle v_A,v_B\rangle := x_A\cdot x_B+y_A\cdot y_B+z_A\cdot z_B.\]

Assume both vectors $v_A$ and $v_B$ are nonzero; suppose that $\phi$ denotes the angle measure between them. Then the scalar product can be expressed the following way:

\[\langle v_A,v_B\rangle=|v_A|\cdot|v_B|\cdot\cos\phi, \]

where

$\begin{aligned} |v_A|&=\sqrt{x_A^2+y_A^2+z_A^2}, & |v_B|&=\sqrt{x_B^2+y_B^2+z_B^2}.\end{aligned}$

Now, assume that the points $A$ and $B$ lie on the unit sphere $\Sigma$ in $\mathbb{R}^3$ centered at the origin. In this case $|v_A|=|v_B|=1$. By 16.2.2 we get that

\[\cos AB_s=\langle v_A,v_B\rangle.\]

Exercise $\PageIndex{1}$

AShow that if $\triangle_s ABC$ is a spherical triangle with a right angle at $C$, and $AC_s=BC_s=\dfrac{\pi}{4}$, then $AB_s=\dfrac{\pi}{3}$.

Hint

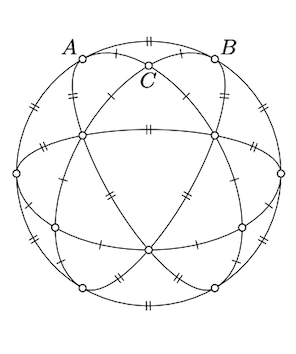
$截屏2021-02-26 上午11.24.50.png$

Applying the Pythagorean theorem, we get that

$\cos AB_s = \cos AC_s \cdot \cos BC_s = \dfrac{1}{2}.$

Therefore, $AB_s = \dfrac{\pi}{3}.$

Alternatively, look at the tessellation of a hemisphere on the picture; it is made from 12 copies of $\triangle_s ABC$ and yet 4 equilateral spherical triangles. From the symmetry of this tessellation, it follows that $[AB]_s$ occupies $\dfrac{1}{6}$ of the equator; that is, $AB_s = \dfrac{\pi}{3}$.